Wprowadzenie do dystrybucji rayleigha
Rozkład Rayleigha to ciągły rozkład prawdopodobieństwa używany do modelowania zmiennych losowych , które mogą przyjmować tylko wartości równe lub większe od zera.
Ma następującą funkcję gęstości prawdopodobieństwa:
f(x; σ) = (x/σ 2 )e -x 2 /(2σ 2 )
gdzie σ jest parametrem skali rozkładu.
Własności rozkładu Rayleigha
Rozkład Rayleigha ma następujące właściwości:
- Średnia: σ√ π/2
- Odchylenie: ((4-π)/2)σ 2
- Tryb: σ
Ponieważ π ma znaną wartość liczbową, możemy uprościć właściwości w następujący sposób:
- Średnia: 1,253σ
- Odchylenie: 0,429σ 2
- Tryb: σ
Wizualizacja rozkładu Rayleigha
Poniższy wykres przedstawia kształt rozkładu Rayleigha, gdyż przyjmuje on różne wartości parametru skali:
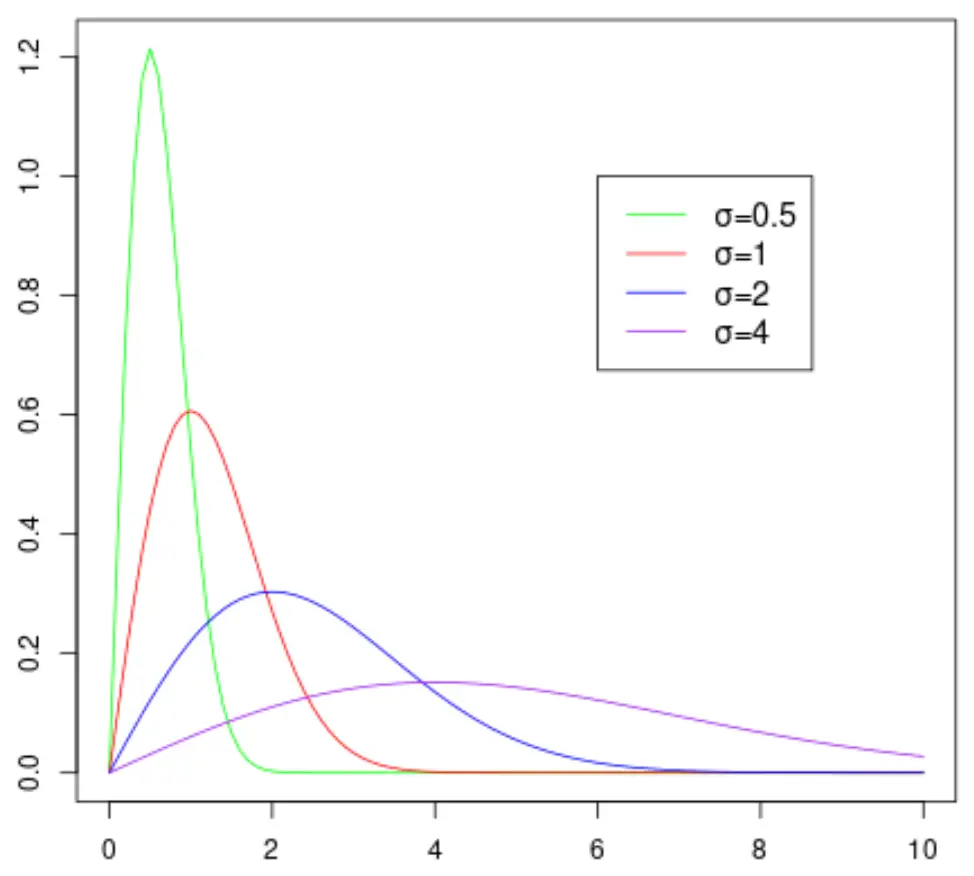
Należy zauważyć, że im większa jest wartość parametru skali σ, tym szerszy staje się rozkład.
Bonus: Dla tych, którzy są ciekawi, użyliśmy następującego kodu R do wygenerowania powyższego wykresu:
#load VGAM package library (VGAM) #create density plots curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green') curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE) curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE) curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE) #add legend legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"), col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)
Związek z innymi dystrybucjami
Rozkład Rayleigha ma następujący związek z innymi rozkładami prawdopodobieństwa:
1. Gdy parametr skali (σ) jest równy 1, rozkład Rayleigha jest równy rozkładowi Chi-kwadrat z 2 stopniami swobody.
2. Rozkład Rayleigha jest szczególnym przypadkiem rozkładu Weibulla z parametrem kształtu k = 2.
3. Rozkład Rayleigha z parametrem skali σ jest równy rozkładowi Ryżu z Ryżem (0, σ).
Aplikacje
W praktyce rozkład Rayleigha jest wykorzystywany w różnych zastosowaniach, w tym:
1. Rozkład Rayleigha służy do modelowania zachowania fal w oceanie, w tym czasu potrzebnego falom na dotarcie do grzbietu i maksymalnej wysokości, jaką osiągają fale.
2. Rozkład Rayleigha służy do modelowania zachowania danych tła w obrazowaniu metodą rezonansu magnetycznego, bardziej znanego jako MRI.
3. Rozkład Rayleigha jest stosowany w żywieniu do modelowania zależności pomiędzy poziomem składników odżywczych a reakcją żywieniową u ludzi i zwierząt.
Dodatkowe zasoby
Poniższe tutoriale dostarczają dodatkowych informacji o innych dystrybucjach w statystykach:
Wprowadzenie do rozkładu normalnego
Wprowadzenie do rozkładu dwumianowego
Wprowadzenie do rozkładu Poissona