Rozkład t-studenta

W tym artykule wyjaśniono, czym jest rozkład t-Studenta i do czego się go używa. Dodatkowo pokazano wykres rozkładu t-Studenta oraz jakie są cechy charakterystyczne tego typu rozkładu prawdopodobieństwa.

Jaka jest dystrybucja Studenta?

Rozkład t-Studenta jest rozkładem prawdopodobieństwa szeroko stosowanym w statystyce. W szczególności rozkład t-Studenta jest używany w teście t-Studenta w celu określenia różnicy między średnimi z dwóch próbek i ustalenia przedziałów ufności.

Rozkład t-Studenta został opracowany przez statystyka Williama Sealy’ego Gosseta w 1908 roku pod pseudonimem „Student”.

Rozkład t-Studenta definiuje się jako liczbę stopni swobody otrzymaną poprzez odjęcie jednej jednostki od całkowitej liczby obserwacji. Zatem wzór na określenie stopni swobody rozkładu t-Studenta to ν=n-1 .

Wykres rozkładu t Studenta

Teraz, gdy znamy już definicję rozkładu t-Studenta, zobaczmy, jaki jest jego wykres. Zatem poniżej można graficznie zobaczyć kilka przykładów rozkładów t-Studenta o różnych stopniach swobody.

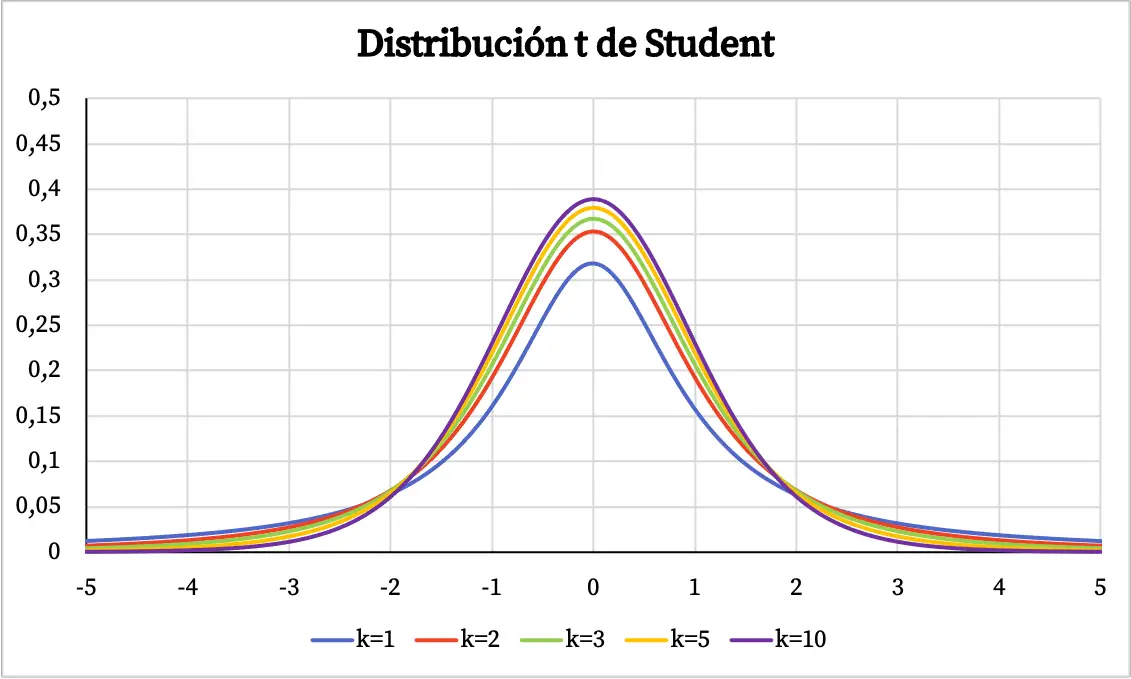
Z wykresu rozkładu t-Studenta można wywnioskować następujące własności:

• Rozkład t-Studenta jest symetryczny ze środkiem w punkcie 0 i ma kształt dzwonu.
• Rozkład t-Studenta jest bardziej rozproszony niż rozkład normalny, to znaczy krzywa rozkładu t-Studenta jest szersza.
• Im więcej stopni swobody ma rozkład t-Studenta, tym mniejsze jest jego rozproszenie.

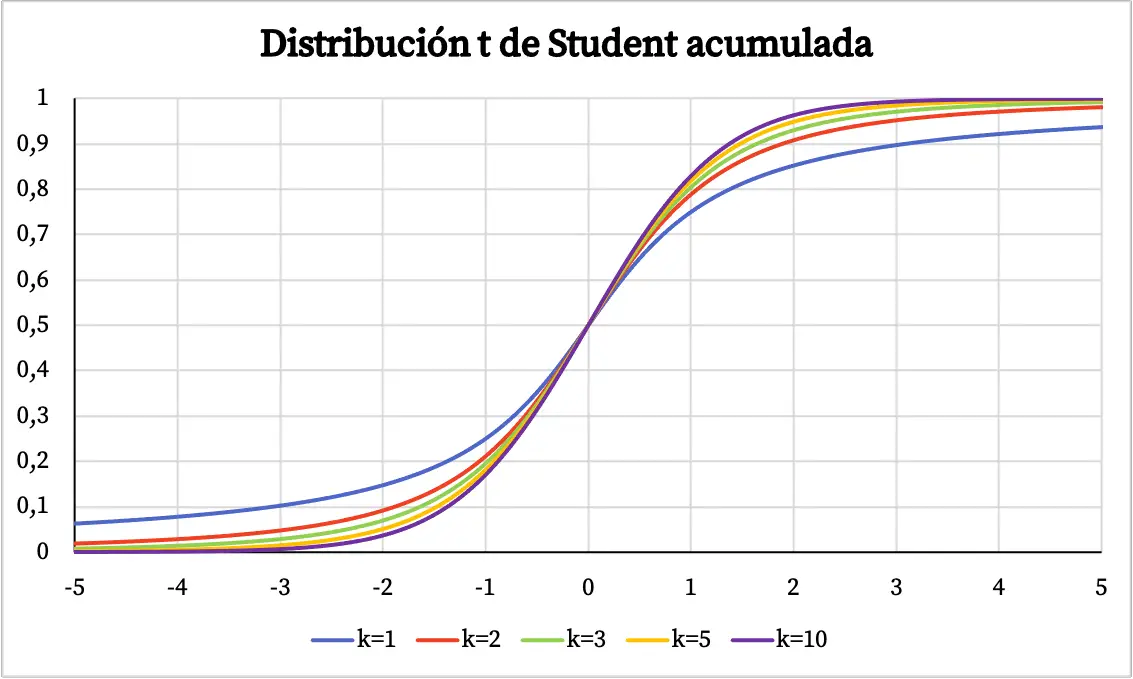
Na powyższym wykresie funkcję gęstości rozkładu t-Studenta przedstawiono w funkcji stopni swobody. Jednakże poniżej można zobaczyć, jak zmienia się skumulowana funkcja prawdopodobieństwa rozkładu t-Studenta:

Charakterystyka rozkładu t-Studenta

Poniżej przedstawiono najważniejsze charakterystyki rozkładu t-Studenta.

• Dziedzina rozkładu t-Studenta składa się z liczb rzeczywistych.

• Dla rozkładów t-Studenta o więcej niż jednym stopniu swobody średnia rozkładu jest równa 0.

• Funkcję gęstości rozkładu t-Studenta definiuje następujący wzór:

• Skumulowaną funkcję rozkładu prawdopodobieństwa rozkładu t-Studenta definiuje następujący wzór:

• Dla rozkładów t-Studenta o stopniach swobody większych niż 3 współczynnik asymetrii wynosi zero, ponieważ jest to rozkład symetryczny.

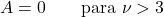
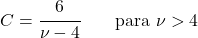Zastosowania rozkładu t-Studenta

Rozkład t-Studenta jest rozkładem prawdopodobieństwa szeroko stosowanym w statystyce. W rzeczywistości istnieje nawet test t-Studenta, który służy do testowania hipotez i przedziałów ufności.

Zatem rozkład t-Studenta pozwala na analizę różnicy pomiędzy średnimi z dwóch próbek, a dokładniej służy do określenia, czy dwie próbki mają znacząco różne średnie. Podobnie test t-Studenta służy do sprawdzenia, czy linia uzyskana z analizy regresji liniowej ma nachylenie, czy nie.

Krótko mówiąc, zastosowania rozkładu t-Studenta opierają się na analizie zbiorów danych, które teoretycznie mają rozkład normalny, ale całkowita liczba obserwacji jest zbyt mała, aby zastosować ten typ rozkładu.