Co to jest dystrybucja erlang?

Rozkład Erlanga jest rozkładem prawdopodobieństwa pierwotnie stworzonym przez AK Erlanga w celu modelowania liczby połączeń telefonicznych, które operator centrali może odebrać jednocześnie.

Dystrybucja jest wykorzystywana w inżynierii ruchu telefonicznego, systemach kolejkowych, biologii matematycznej i innych dziedzinach do modelowania różnorodnych zjawisk w świecie rzeczywistym.

Własności rozkładu Erlanga

Rozkład Erlanga ma następującą funkcję gęstości prawdopodobieństwa:

f(x; k, μ) = x ^k-1 e ^-x/μ / μ ^k (k-1)!

Złoto:

• k: parametr kształtu. Musi to być dodatnia liczba całkowita.
• μ: Parametr skali. Musi to być dodatnia liczba rzeczywista.

Okazuje się, że rozkład Erlanga jest szczególnym przypadkiem rozkładu Gamma, gdy parametr kształtu k jest ograniczony tylko do dodatnich liczb całkowitych rzeczywistych.

Należy zauważyć, że parametr skali jest odwrotnością parametru szybkości λ, tj. μ = 1/λ.

Rozkład Erlanga ma następujące właściwości:

• Średnia: k/λ
• Tryb: (k-1)/λ
• Różnica: k/λ ²
• Asymetria: 2/√k
• Spłaszczenie: 6/k

Dystrybucja Erlanga ma następujące powiązania z innymi dystrybucjami:

• Gdy parametr kształtu k jest równy 1, rozkład Erlanga jest równy rozkładowi wykładniczemu .
• Gdy parametr skali μ jest równy 2, rozkład Erlanga jest równy rozkładowi Chi-kwadrat z 2 stopniami swobody.

Zobacz dystrybucję Erlanga

Poniższy wykres przedstawia kształt rozkładu Erlanga, gdy przyjmuje on różne parametry:

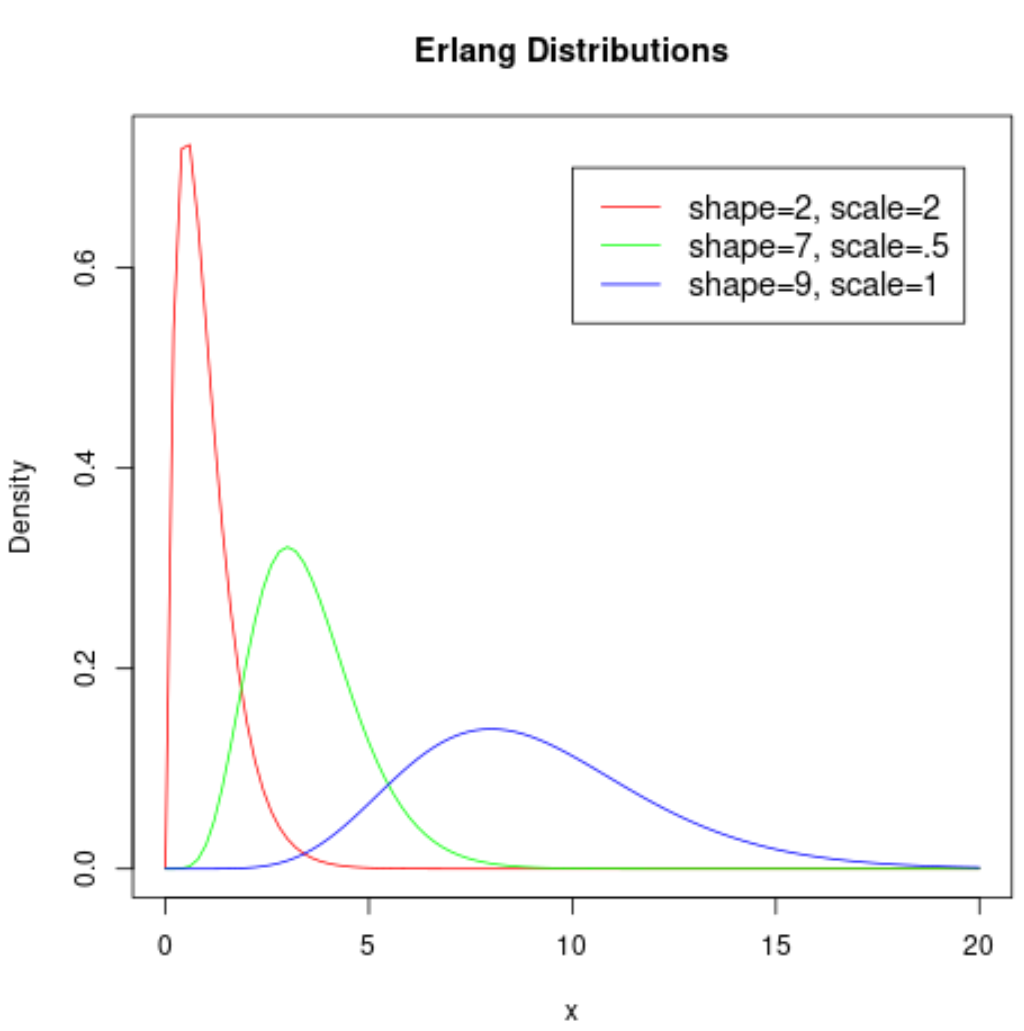
Ciekawie jest zobaczyć, jak bardzo zmienia się kształt rozkładu w zależności od wartości zastosowanych parametrów kształtu i skali.

Uwaga: kod R użyty do wygenerowania wykresu rozkładów Erlanga znajdziesz tutaj .

Przypadek użycia

Dystrybucja Erlang jest używana w różnych kontekstach świata rzeczywistego, w tym:

1. Centra telefoniczne

Rozkład Erlanga służy do modelowania czasu pomiędzy połączeniami przychodzącymi w call center, a także oczekiwanej liczby połączeń.

Dzięki temu call center wiedzą, jaka powinna być ich pojemność kadrowa w różnych porach dnia, aby mogły terminowo obsługiwać połączenia przychodzące bez utraty pieniędzy w wyniku zatrudniania zbyt dużej liczby pracowników na jednej zmianie. dana praca.

2. Parametry medyczne

Rozkład Erlanga jest szeroko stosowany do modelowania rozkładu czasu trwania cyklu komórkowego, który ma wiele różnych zastosowań w środowisku medycznym.

3. Ustawienia sprzedaży detalicznej

Dystrybucja Erlanga jest wykorzystywana przez sprzedawców detalicznych do modelowania częstotliwości opóźnień w zakupach konsumenckich.

Daje to sprzedawcom detalicznym i innym firmom pojęcie, jak często dany konsument powinien kupować od nich produkt lub usługę. Pomaga to firmom kontrolować zapasy, a także rekrutować pracowników.

Dodatkowe zasoby

Wprowadzenie do rozkładu normalnego
Wprowadzenie do rozkładu dwumianowego
Wprowadzenie do rozkładu Poissona