Dystrybucja weibula

Przez Benjamin Anderson 3 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład Weibulla i do czego się go używa. Dodatkowo będziesz mógł zobaczyć graficzną reprezentację rozkładu Weibulla i jakie są właściwości tego typu rozkładu prawdopodobieństwa.

Co to jest rozkład Weibulla?

Rozkład Weibulla jest ciągłym rozkładem prawdopodobieństwa zdefiniowanym przez dwa charakterystyczne parametry: parametr kształtu α i parametr skali λ.

W statystyce rozkład Weibulla jest używany głównie do analizy przeżycia. Podobnie rozkład Weibulla ma wiele zastosowań w różnych dziedzinach. Poniżej omówimy szczegółowo korzystanie z rozkładu Weibulla.

$X\sim\text{Weibull}(\alpha,\lambda)$

Zdaniem autorów rozkład Weibulla można również parametryzować za pomocą trzech parametrów. Następnie dodawany jest trzeci parametr zwany wartością progową, który wskazuje odciętą, od której zaczyna się wykres rozkładu.

Rozkład Weibulla został nazwany na cześć Szweda Waloddiego Weibulla, który szczegółowo go opisał w 1951 r. Jednakże rozkład Weibulla został odkryty przez Maurice’a Frécheta w 1927 r., a po raz pierwszy zastosowany przez Rosina i Rammlera w 1933 r.

Wykreślanie rozkładu Weibulla

Kiedy już zapoznamy się z definicją rozkładu Weibulla, zobaczymy, jak zmienia się jego graficzna reprezentacja w zależności od wartości jego parametrów.

Poniżej możesz zobaczyć kilka przykładów tego, jak wykres funkcji gęstości rozkładu Weibulla zmienia się w zależności od wartości parametru kształtu i parametru skali.

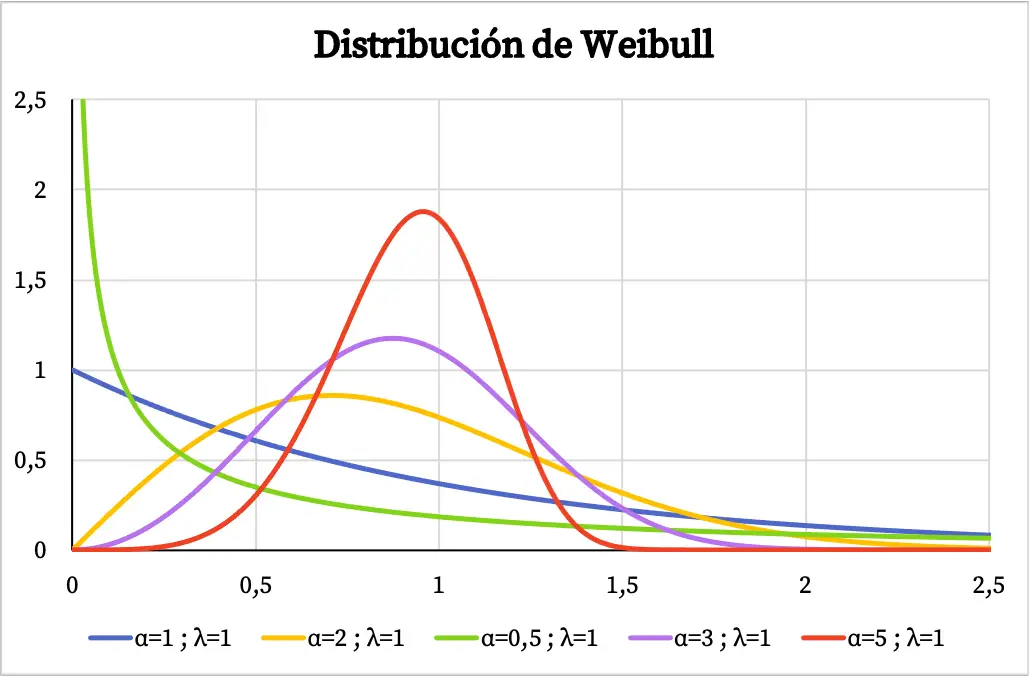
Gdy do modelowania awaryjności systemu w funkcji czasu stosuje się rozkład Weibulla, wartość parametru kształtu α oznacza, co następuje:

α<1: wskaźnik awaryjności maleje z czasem.
α=1: wskaźnik awaryjności jest stały w czasie.
α>1: wskaźnik awaryjności wzrasta z czasem.

Z drugiej strony na poniższym wykresie można zobaczyć skumulowaną funkcję prawdopodobieństwa rozkładu Weibulla wykreśloną na podstawie jego charakterystycznych wartości.

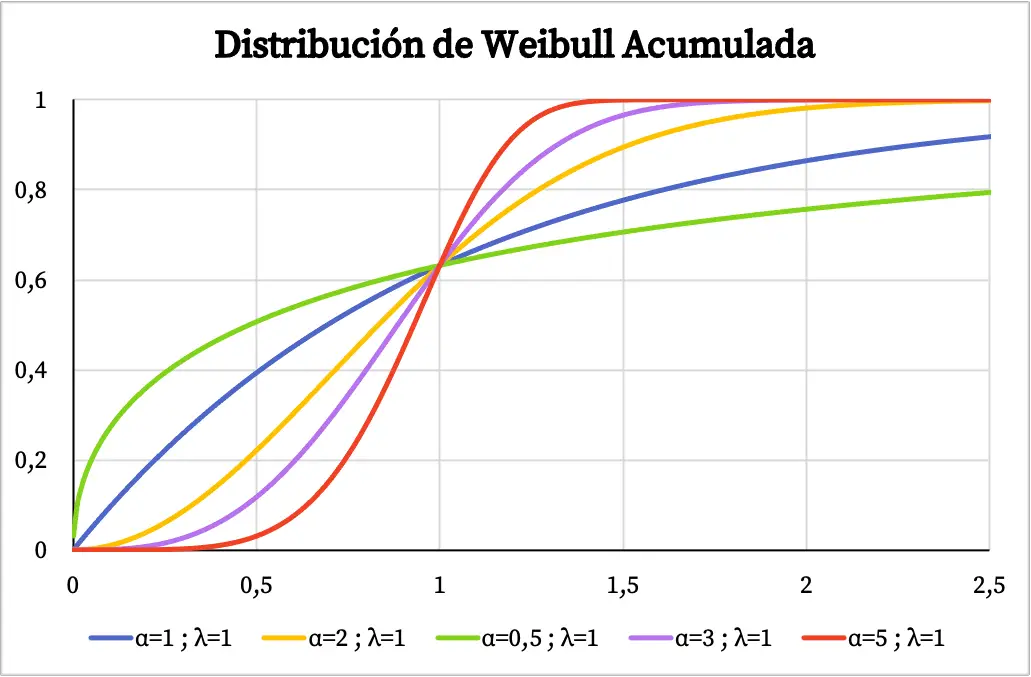
skumulowane prawdopodobieństwo rozkładu Weibulla

Charakterystyka rozkładu Weibulla

Rozkład Weibulla ma następujące cechy:

Rozkład Weibulla ma dwa charakterystyczne parametry definiujące jego wykres: parametr kształtu α i parametr skali λ. Obydwa parametry są dodatnimi liczbami rzeczywistymi.

$\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=”Rendered by QuickLaTeX.com” height=”92″ width=”101″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Rozkład Weibulla akceptuje tylko dodatnie wartości odciętych.</li> </ul> <p class=$ $x\in (0,+\infty)$

Średnią rozkładu Weibulla oblicza się za pomocą następującego wzoru:

$\displaystyle E[X]=\frac{1}{\lambda}\;\Gamma\left(1+\frac{1}{\alpha}\right)$

Z drugiej strony wzór na znalezienie wariancji rozkładu Weibulla to:

$\displaystyle Var(X)=\frac{1}{\lambda^2}\left[\Gamma\left(1+\frac{2}{\alpha}\right)-\Gamma^2\left(1+\frac{1}{\alpha}\right)\right]$

Tryb zmiennej losowej zgodny z rozkładem Weibulla o α>1 można określić za pomocą następującego wyrażenia:

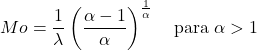
$\displaystyle Mo=\frac{1}{\lambda}\left(\frac{\alpha-1}{\alpha} \right)^{\frac{1}{\alpha}} \quad \text{para } \alpha>1″ title=”Rendered by QuickLaTeX.com” height=”50″ width=”257″ style=”vertical-align: -17px;”></p> </p> <ul> <li> Wzór na funkcję gęstości rozkładu Weibulla to:</li> </ul> <p class=$ $\displaystyle P[X=x]=\lambda\alpha(\lambda x)^{\alpha-1}e^{-(\lambda x)^\alpha}$

Podobnie wzór na skumulowaną funkcję prawdopodobieństwa rozkładu Weibulla wygląda następująco:

$\displaystyle P[X\leq x]=1- e^{-(\lambda x)^\alpha}$

Współczynnik asymetrii rozkładu Weibulla oblicza się stosując następujący wzór:

$\displaystyle A=\frac{\displaystyle\Gamma\left(1+\frac{3}{\alpha}\right)\frac{|}{\lambda^3}-3\mu\sigma^2-\mu^3}{\sigma^3}$

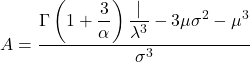
Ostatecznie wzór pozwalający wyznaczyć współczynnik kurtozy rozkładu Weibulla jest następujący:

$\displaystyle C=\frac{\displaystyle\frac{1}{\lambda^4}\Gamma \left(1+\frac{4}{\alpha}\right)-4\gamma_{1}\sigma^3\mu-6\mu^2\sigma^2-\mu^4}{\sigma^4}$

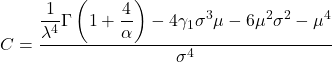
Złoto

$\Gamma_i=\Gamma\left(1+\frac{i}{\alpha}\right).$

Zastosowania rozkładu Weibulla

Dystrybucja Weibulla ma wiele zastosowań, w tym:

W statystyce stosowanej do analizy przeżycia wykorzystuje się rozkład Weibulla.
W inżynierii rozkład Weibulla służy do modelowania funkcji związanych z czasem produkcji.
W systemach radarowych do symulacji rozproszenia odbieranego sygnału.
W branży ubezpieczeniowej do modelowania wysokości roszczeń.
Na przykład w meteorologii do modelowania częstotliwości różnych prędkości wiatru.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej