Excel: utwórz statystyczne porównanie dwóch zestawów danych

Często możesz chcieć przeprowadzić porównanie statystyczne dwóch zestawów danych w Excelu, aby zrozumieć, jak różni się rozkład wartości w każdym zestawie danych.

Istnieją dwa popularne sposoby przeprowadzania porównań statystycznych:

Metoda 1: Oblicz pięciocyfrowe podsumowanie każdego zestawu danych

Możemy obliczyć pięciocyfrowe podsumowanie każdego zbioru danych, które składa się z następujących wartości:

• Wartość minimalna
• Pierwszy kwartyl (25. percentyl)
• Mediana (50. percentyl)
• Trzeci kwartyl (75. percentyl)
• Maksymalny

Obliczając te pięć wartości, możemy dobrze zrozumieć rozkład wartości w każdym zestawie danych.

Metoda 2: Oblicz średnią i odchylenie standardowe

Prostszym sposobem statystycznego porównania dwóch zestawów danych jest obliczenie średniej i odchylenia standardowego każdego zestawu danych.

Pomaga nam to w przybliżeniu zrozumieć, gdzie znajduje się „centralna” wartość i jaki jest rozkład wartości w każdym zestawie danych.

Poniższy przykład pokazuje, jak zastosować każdą z tych metod w praktyce.

Przykład: Wykonaj statystyczne porównanie dwóch zestawów danych w programie Excel

Załóżmy, że mamy w Excelu dwa zestawy danych, które pokazują wyniki uczniów z dwóch różnych klas uzyskane na konkretnym egzaminie:

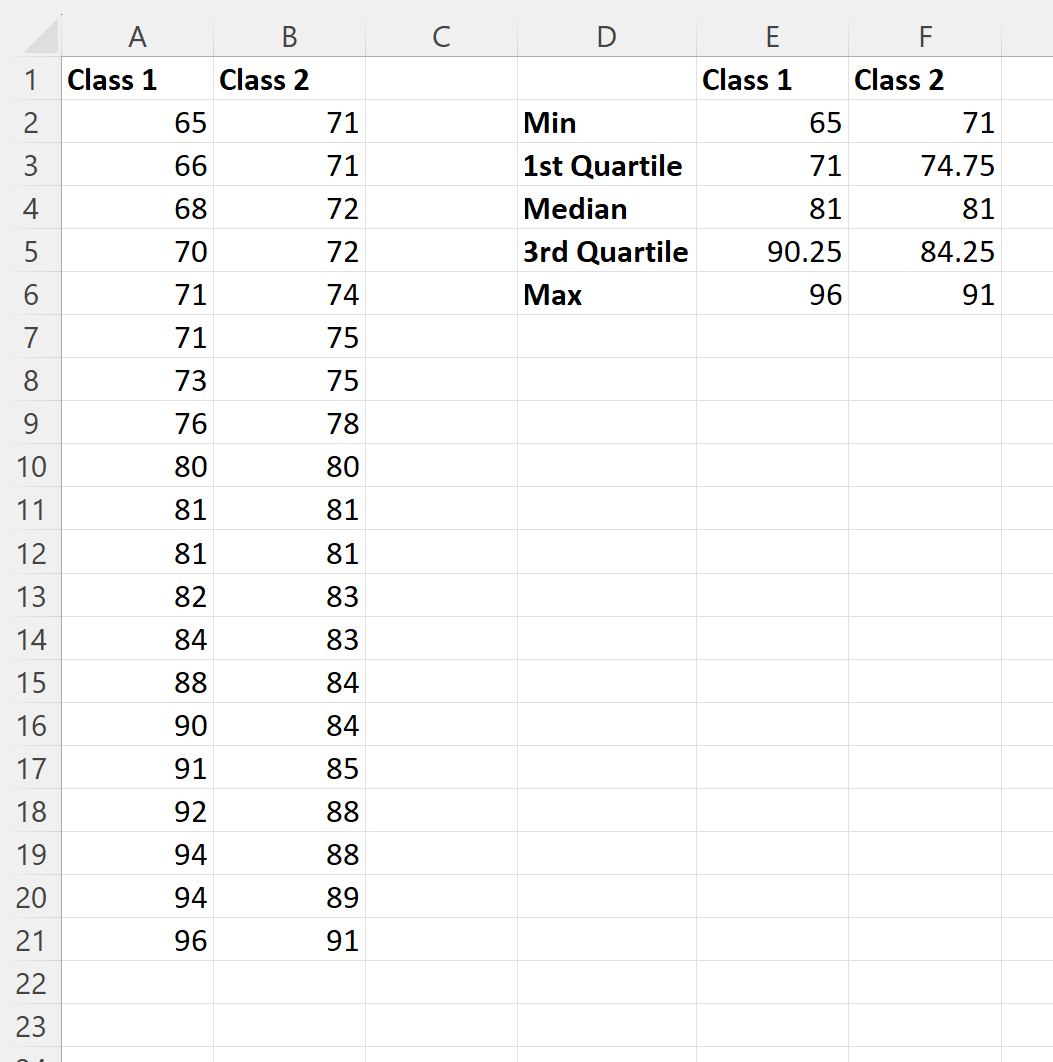
W komórkach kolumny E możemy wpisać następujące wzory, aby obliczyć pięciocyfrowe podsumowanie wyników egzaminu dla klasy 1:

• E2 : =MIN(A2:A21)
• E3 : =KWARTYL(A2:A21, 1)
• E4 : =MEDIANA(A2:A21)
• E5 : =KWARTYL(A2:A21, 3)
• E6 : =MAX(A2:A21

Możemy następnie kliknąć i przeciągnąć te formuły w prawo, aby obliczyć te same wartości dla klasy 2:

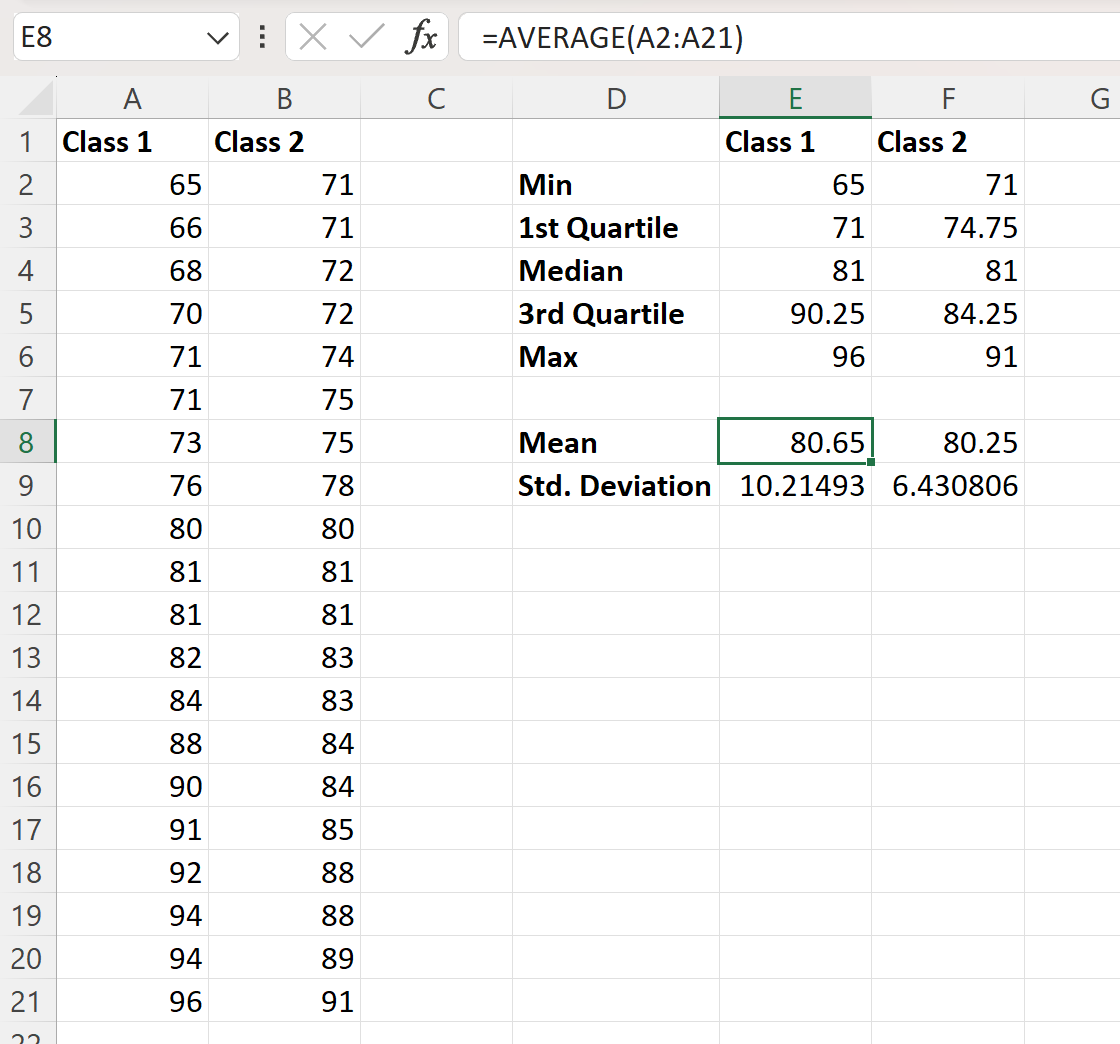
Możemy wówczas wpisać do komórek kolumny E następujące wzory, aby obliczyć średnią i odchylenie standardowe wyników egzaminu dla klasy 1:

• E8 : =ŚREDNIA(A2:A21)
• E9 : =ETDEV(A2:A21, 1)

Możemy następnie kliknąć i przeciągnąć te formuły w prawo, aby obliczyć te same wartości dla klasy 2:

Z tego statystycznego porównania dwóch zbiorów danych możemy wyciągnąć następujące wnioski:

Wniosek 1: Obydwa zbiory danych mają podobną wartość „podstawową”.

W obu zbiorach danych mediana wyników egzaminu wynosi 81. Wartości średnie różnią się tylko nieznacznie: pierwsza klasa ma średni wynik egzaminu 80,65, druga klasa ma średni wynik egzaminu 80,65, podczas gdy druga klasa ma średni wynik egzaminu 80,65 'recenzja 80,25.

To mówi nam, że „podstawowy” lub „typowy” wynik egzaminu w obu klasach jest podobny.

Wniosek 2: Pierwszy zbiór danych charakteryzuje się znacznie większym „rozproszeniem” wartości.

Kilka wskaźników mówi nam, że wyniki egzaminów pierwszej klasy są znacznie bardziej rozproszone niż te drugiej klasy.

Przykładowo zakres klasy 1 jest znacznie większy:

• Zakres klasy 1: 96 – 65 = 31
• Zakres klasy 2: 91 – 71 = 20

Rozstęp międzykwartylowy klasy 1 jest również znacznie wyższy:

• Rozstęp międzykwartylowy klasy 1: 90,25 – 71 = 19,25
• Rozstęp międzykwartylowy klasy 2: 84,25 – 74,75 = 9,5

Odchylenie standardowe klasy 1 jest również znacznie wyższe:

• Odchylenie standardowe klasy 1: 10,21
• Odchylenie standardowe klasy 2: 6,43

Każdy z tych mierników mówi nam, że różnica w wynikach egzaminów uczniów klasy 1 jest znacznie większa niż w klasie 2.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe operacje w programie Excel:

Jak utworzyć tabelę podsumowującą w programie Excel
Jak obliczyć medianę według grupy w programie Excel
Jak obliczyć odchylenie standardowe i zignorować zero w programie Excel