Jak wykonać test t z nierównymi wariancjami w programie excel

Test t dla dwóch prób służy do określenia, czy średnie z dwóch populacji są równe.

Istnieją dwie wersje dwóch przykładów testu t, których można użyć:

• test t z równymi wariancjami
• test t z nierównymi wariancjami

Testu t z nierównymi wariancjami używamy, gdy wariancje dwóch próbek nie są równe.

Najprostszym sposobem ustalenia, czy wariancje między dwiema próbami są równe, jest skorzystanie z praktycznej reguły wariancji .

Z reguły, jeśli stosunek największej wariancji do najmniejszej wariancji jest mniejszy niż 4, możemy założyć, że wariancje są w przybliżeniu równe.

W przeciwnym razie, jeśli stosunek jest równy lub większy niż 4, przyjmuje się, że wariancje nie są równe.

Poniższy przykład pokazuje krok po kroku, jak przeprowadzić test t dla dwóch próbek z nierównymi wariancjami w programie Excel.

Krok 1: Wprowadź dane

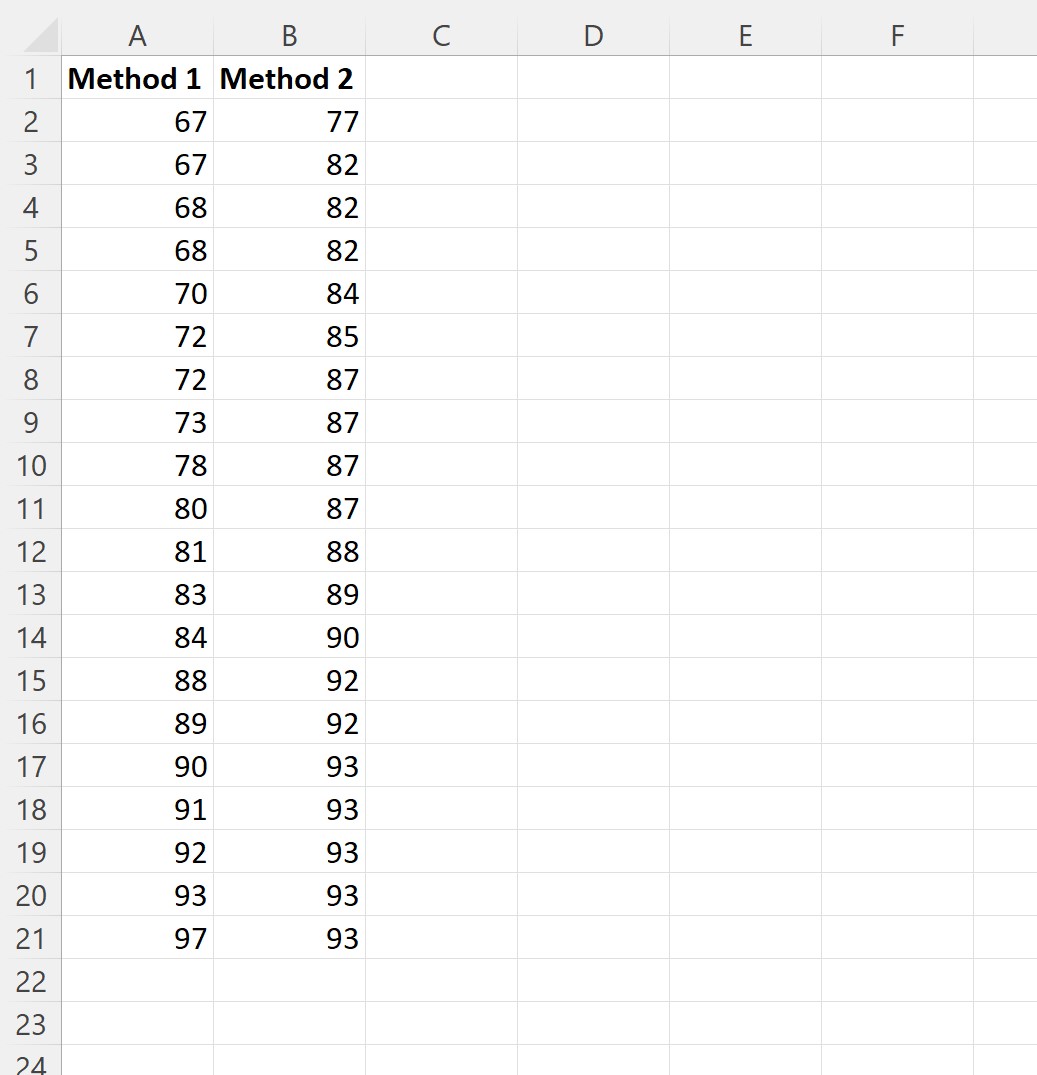
Załóżmy, że chcemy ustalić, czy dwie różne metody studiowania prowadzą do różnych średnich ocen studentów na danej uczelni.

Wybieramy losową próbę 20 uczniów, którzy stosują każdą metodę nauki i rejestrują wyniki egzaminów:

Krok 2: Określ równą lub nierówną wariancję

Następnie możemy obliczyć stosunek wariancji próbki:

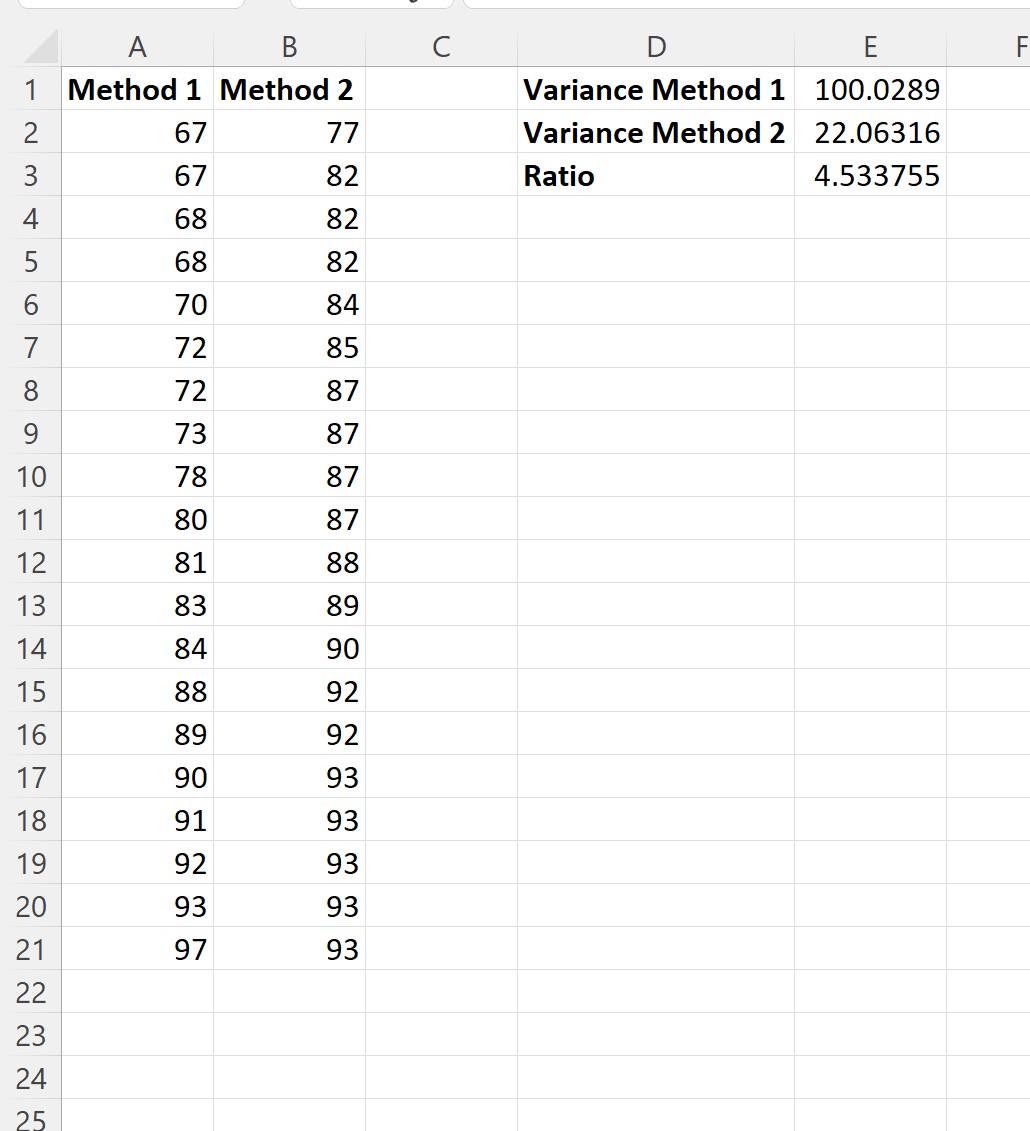
Oto formuły, które wpisaliśmy w każdej komórce:

• Komórka E1: =VAR.S(A2:A21)
• Komórka E2: =VAR.S(B2:B21)
• Komórka E3: =E1/E2

Widzimy, że stosunek największej wariancji próbki do najmniejszej wariancji próbki wynosi 4,533755 .

Jeśli wartość ta jest większa lub równa 4, zakładamy, że wariancje pomiędzy dwiema próbkami nie są równe.

Krok 3: Wykonaj test t dla dwóch próbek z nierówną wariancją

Następnie możemy wykonać test t dla dwóch prób z nierównymi wariancjami, aby określić, czy średni wynik egzaminu między dwiema próbami jest równy.

Aby to zrobić, kliknij zakładkę Dane na górnej wstążce, a następnie kliknij przycisk Analiza danych w grupie Analizuj :

Jeśli nie widzisz tego przycisku, musisz najpierw zainstalować bezpłatny pakiet narzędzi do analizy danych w programie Excel .

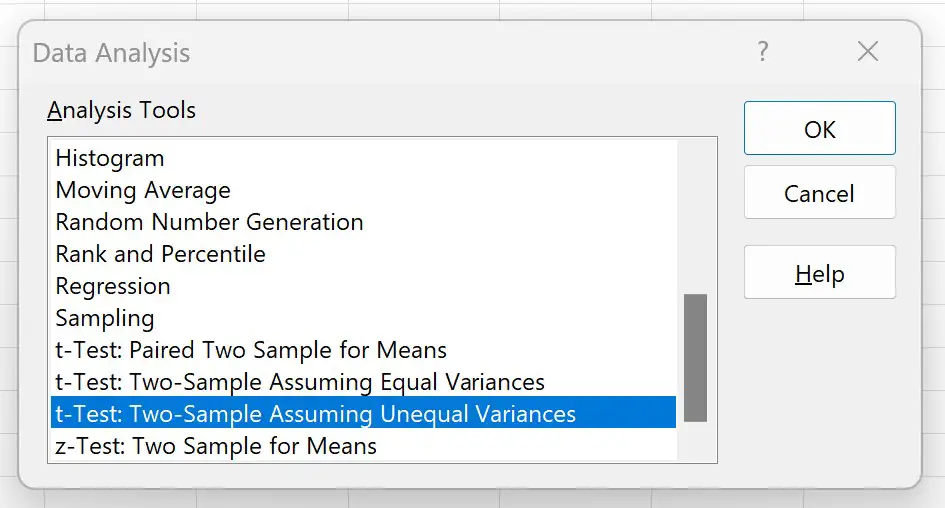
W nowym oknie, które się pojawi, kliknij Test T: Dwie próbki przy założeniu nierównych wariancji , a następnie kliknij OK :

W nowym oknie, które się pojawi, wprowadź następujące informacje, a następnie kliknij OK :

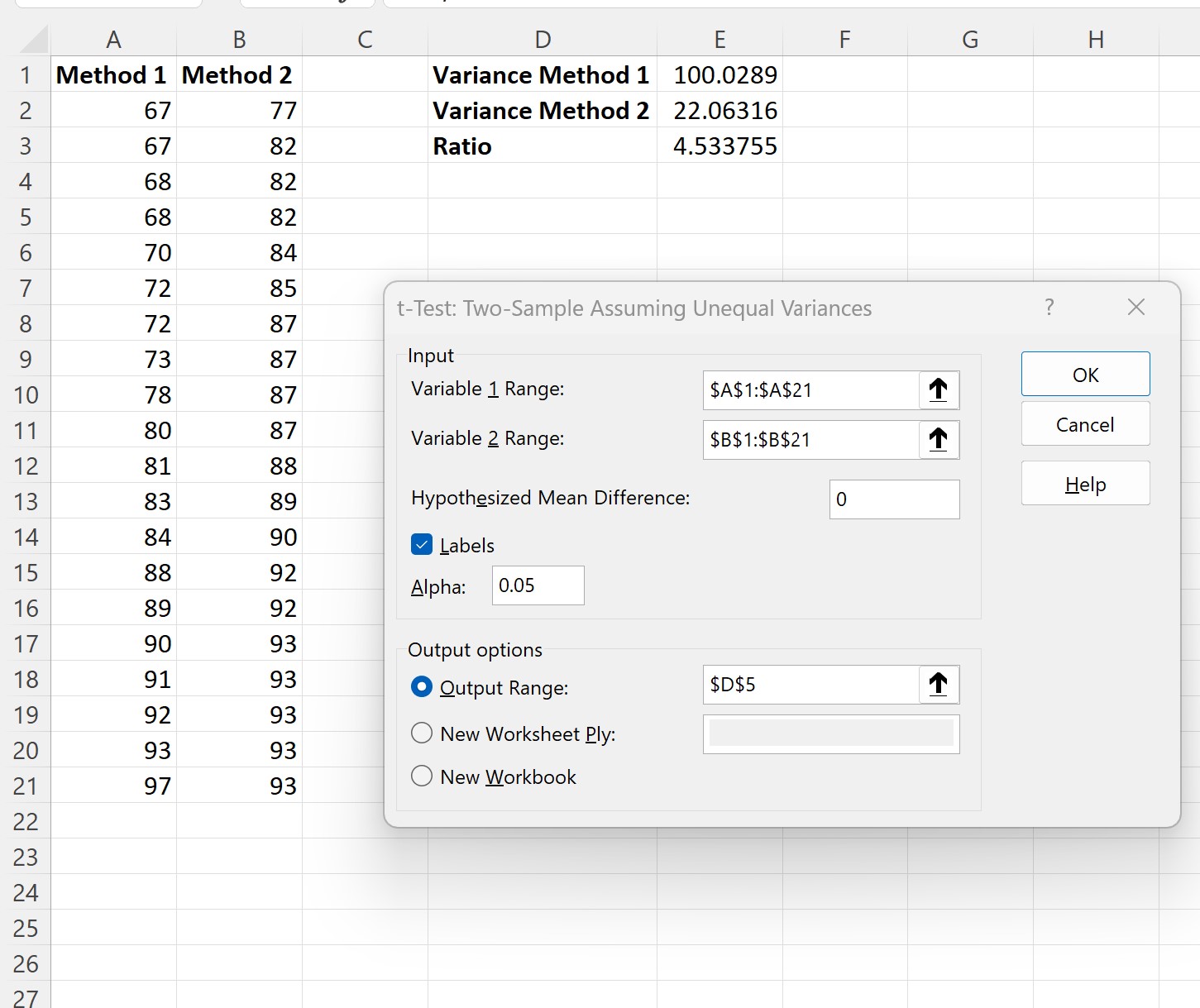
Po kliknięciu OK pojawią się wyniki dwóch przykładów testu t:

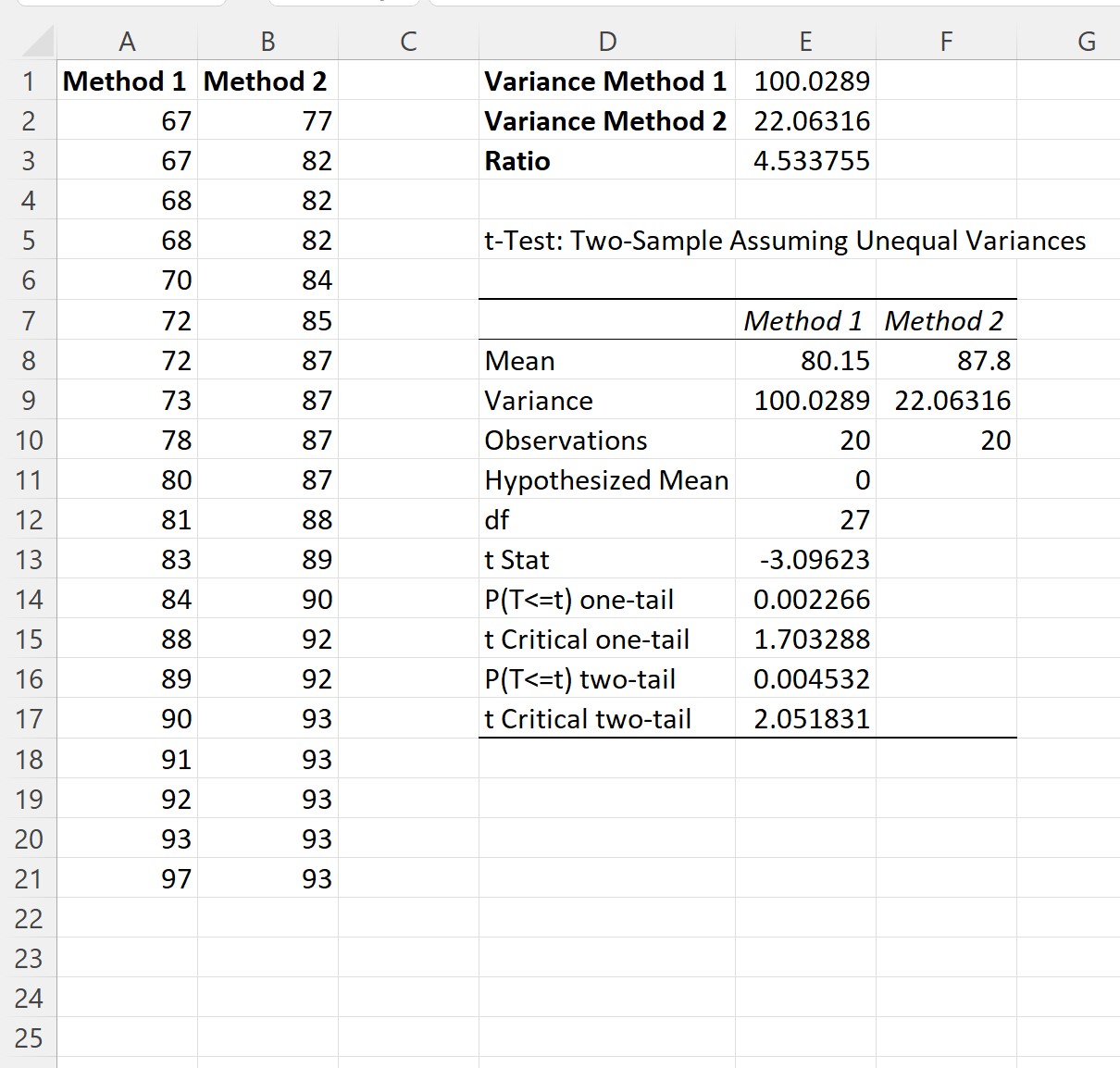
Krok 4: Interpretacja wyników

Z wyniku możemy zobaczyć:

• Średni wynik egzaminu dla Metody 1 wyniósł 80,15 .
• Średni wynik egzaminu dla Metody 2 wyniósł 87,8 .
• Statystyka testu t wyniosła -3,09623 .
• Odpowiednia dwustronna wartość p wyniosła 0,004532 .

Ponieważ ta wartość p jest mniejsza niż 0,05, możemy stwierdzić, że istnieje statystycznie istotna różnica w średnich wynikach egzaminów pomiędzy obiema metodami badania.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w programie Excel:

Jak wykonać test t dla jednej próby w programie Excel
Jak wykonać test t dla par próbek w programie Excel
Jak wykonać jedną próbkę i dwie próbki Z w programie Excel