Jak obliczyć reszty standaryzowane w programie excel

Reszta to różnica między wartością obserwowaną a wartością przewidywaną w modelu regresji .

Oblicza się go w następujący sposób:

Wartość rezydualna = Wartość obserwowana – Wartość przewidywana

Jeśli wykreślimy zaobserwowane wartości i nałożymy dopasowaną linię regresji, resztą dla każdej obserwacji będzie pionowa odległość między obserwacją a linią regresji:

Jeden z typów reszt, którego często używamy do identyfikacji wartości odstających w modelu regresji, nazywany jest resztą standaryzowaną .

Oblicza się go w następujący sposób:

r _ja = mi _ja / s(e _ja ) = mi _ja / RSE√ 1-h _ii

Złoto:

• e _i : i- ^ta reszta
• RSE: resztkowy błąd standardowy modelu
• h _ii : Powstanie i ^-tej obserwacji

W praktyce często za wartość odstającą uznajemy każdą standaryzowaną resztę, której wartość bezwzględna jest większa niż 3.

W tym samouczku przedstawiono krok po kroku przykład obliczania reszt standardowych w programie Excel.

Krok 1: Wprowadź dane

Najpierw wprowadzimy wartości z małego zbioru danych do Excela:

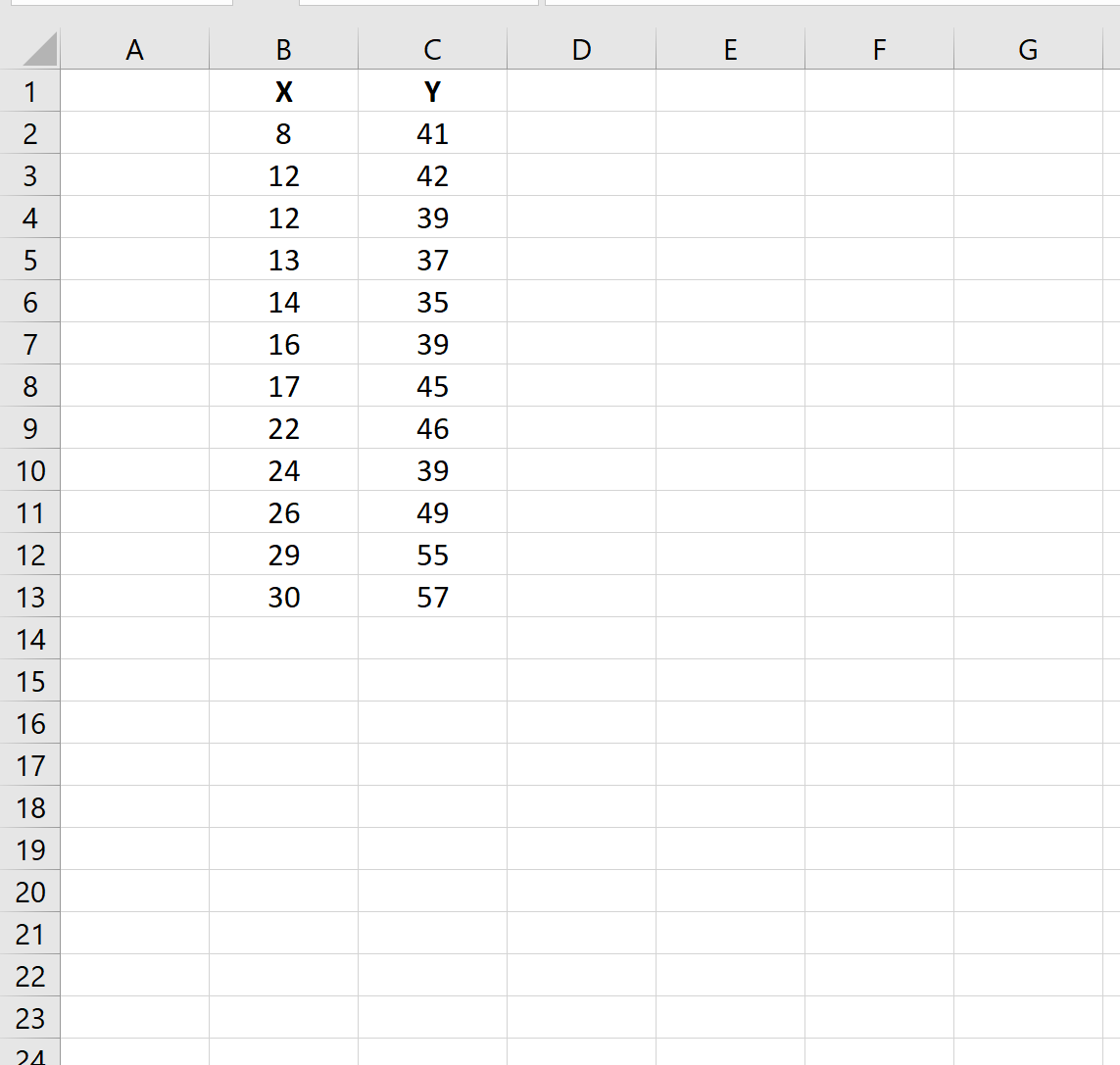
Krok 2: Oblicz reszty

Następnie przejdziemy do karty Dane na górnej wstążce i klikniemy Analiza danych w grupie Analiza :

Jeśli jeszcze nie zainstalowałeś tego dodatku, zapoznaj się z tym samouczkiem, aby dowiedzieć się, jak to zrobić. Jest łatwy w instalacji i całkowicie darmowy.

Po kliknięciu Analiza danych kliknij opcję Regresja , a następnie kliknij OK . W nowym oknie, które się pojawi, wprowadź następujące informacje i kliknij OK :

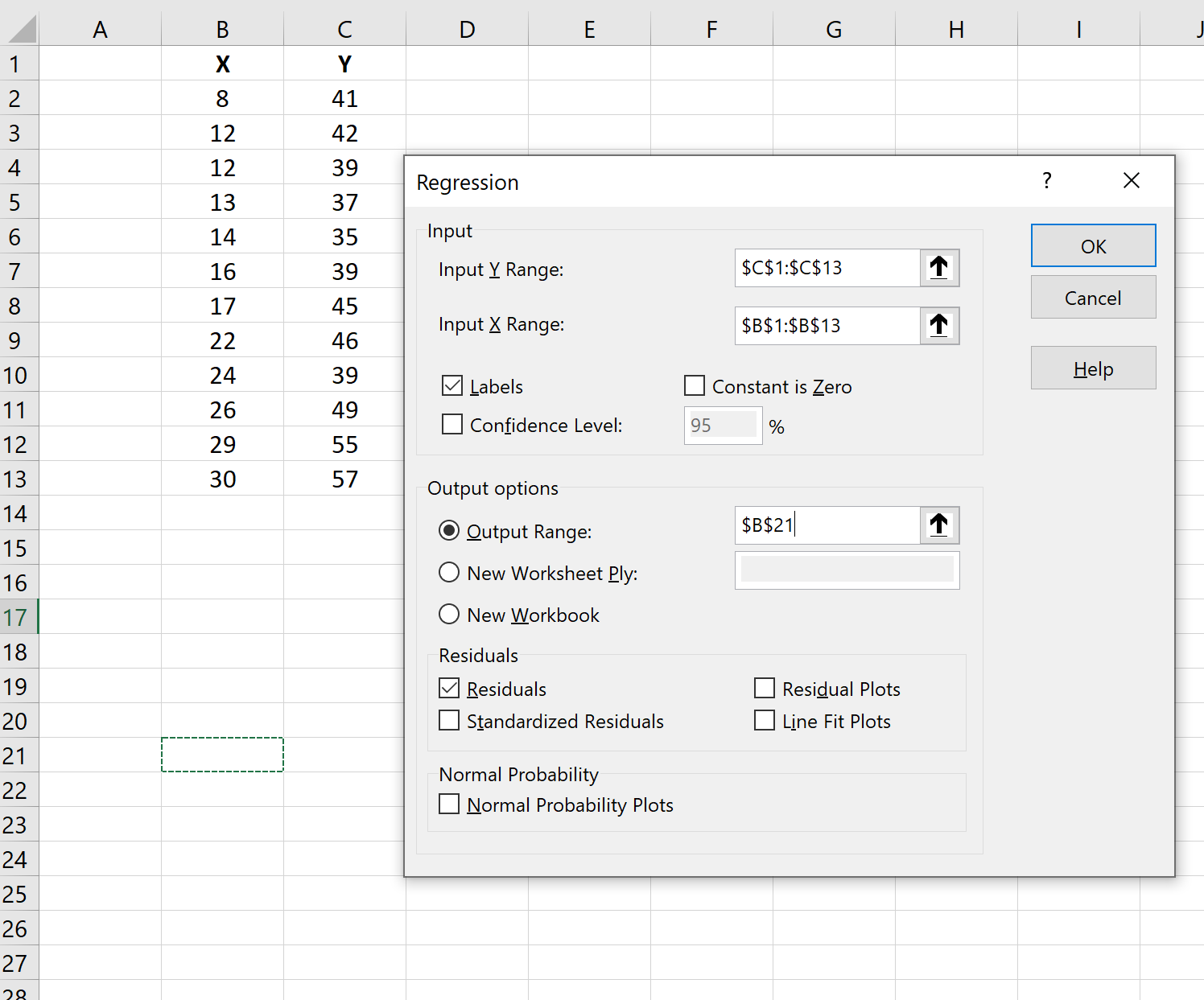
Reszta dla każdej obserwacji pojawi się w wyniku:

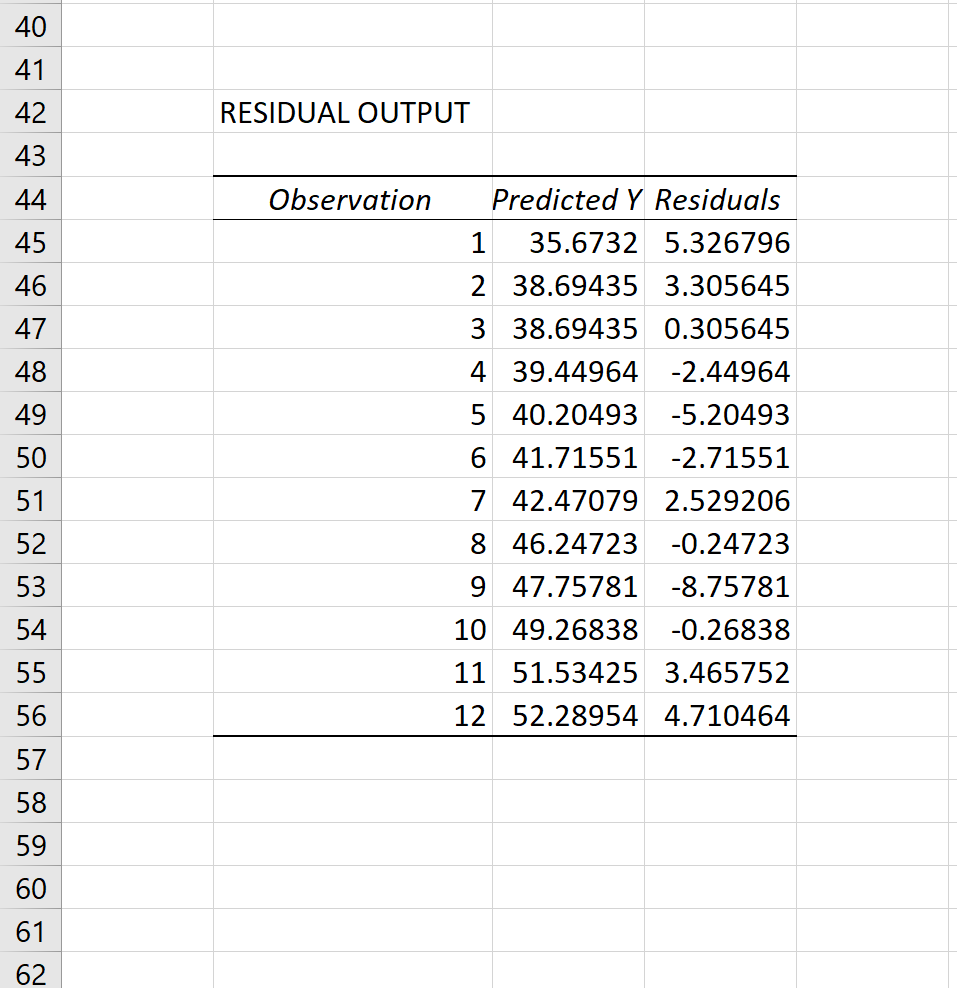
Skopiuj i wklej te pozostałości do nowej kolumny obok oryginalnych danych:

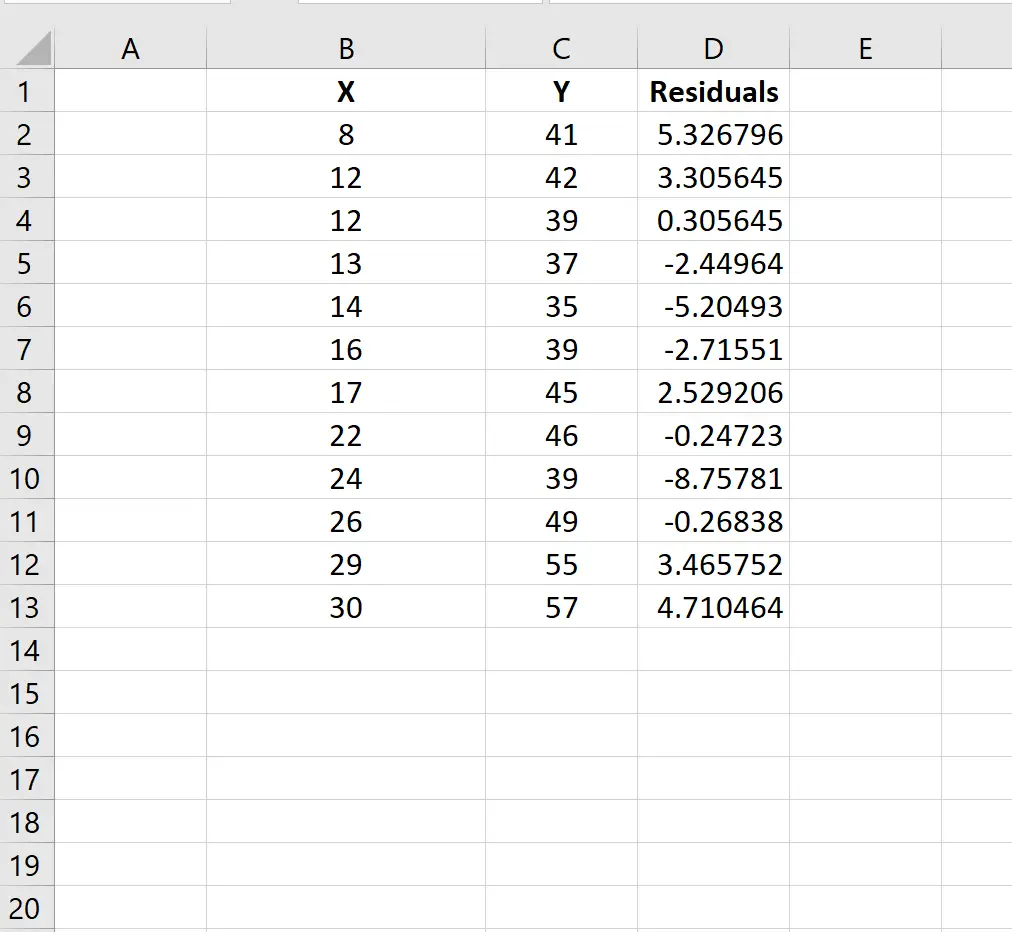
Krok 3: Oblicz dźwignię

Następnie musimy obliczyć dźwignię każdej obserwacji.

Poniższy obraz pokazuje, jak to zrobić:

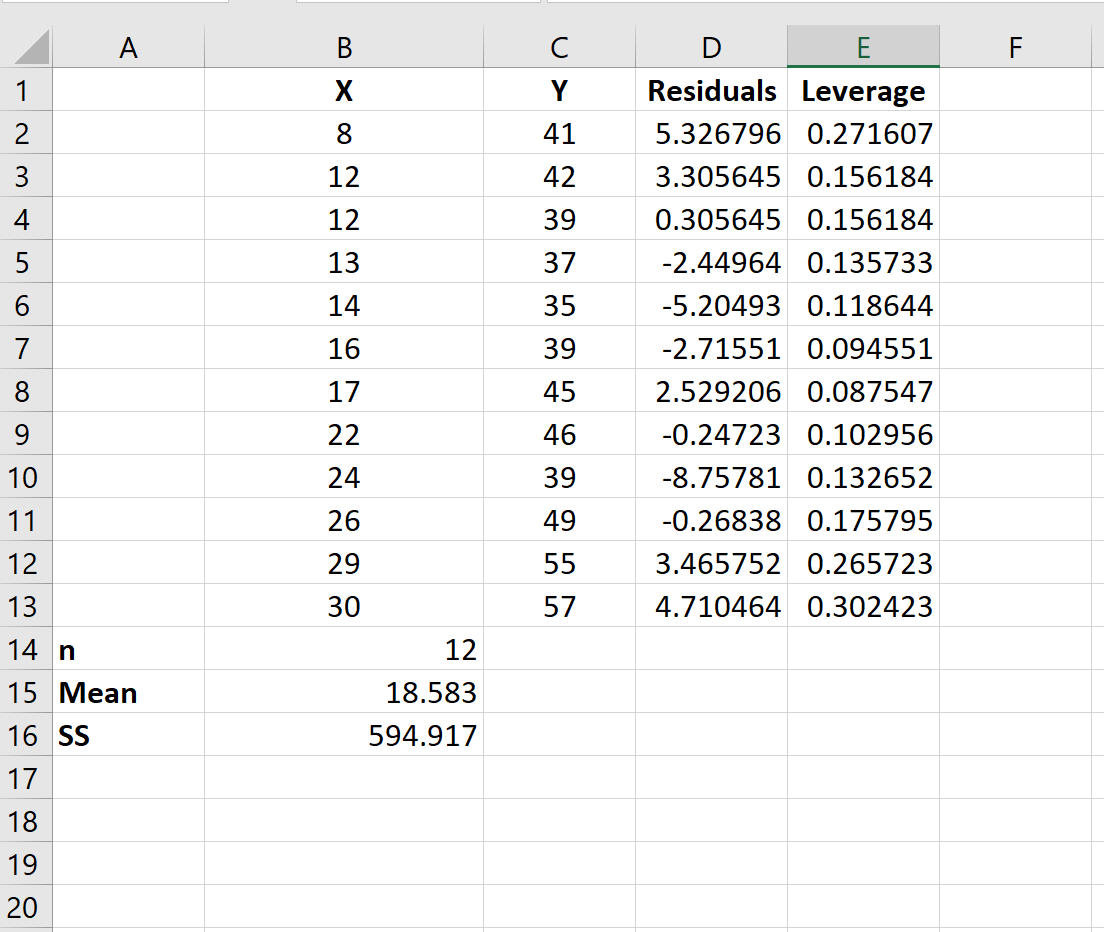
Oto formuły używane w różnych komórkach:

• B14: = LICZBA (B2: B13)
• B15: = ŚREDNIA (B2: B13)
• B16: =DEVSQ(B2:B13)
• E2: =1/B$14+(B2-$B$15)^2/B$16

Krok 4: Oblicz reszty standaryzowane

Na koniec możemy obliczyć reszty standaryzowane za pomocą wzoru:

r _ja = mi _ja / RSE√ 1-h _ii

CSR modelu można znaleźć w wynikach poprzedniego modelu. Okazuje się, że jest to 4,44 :

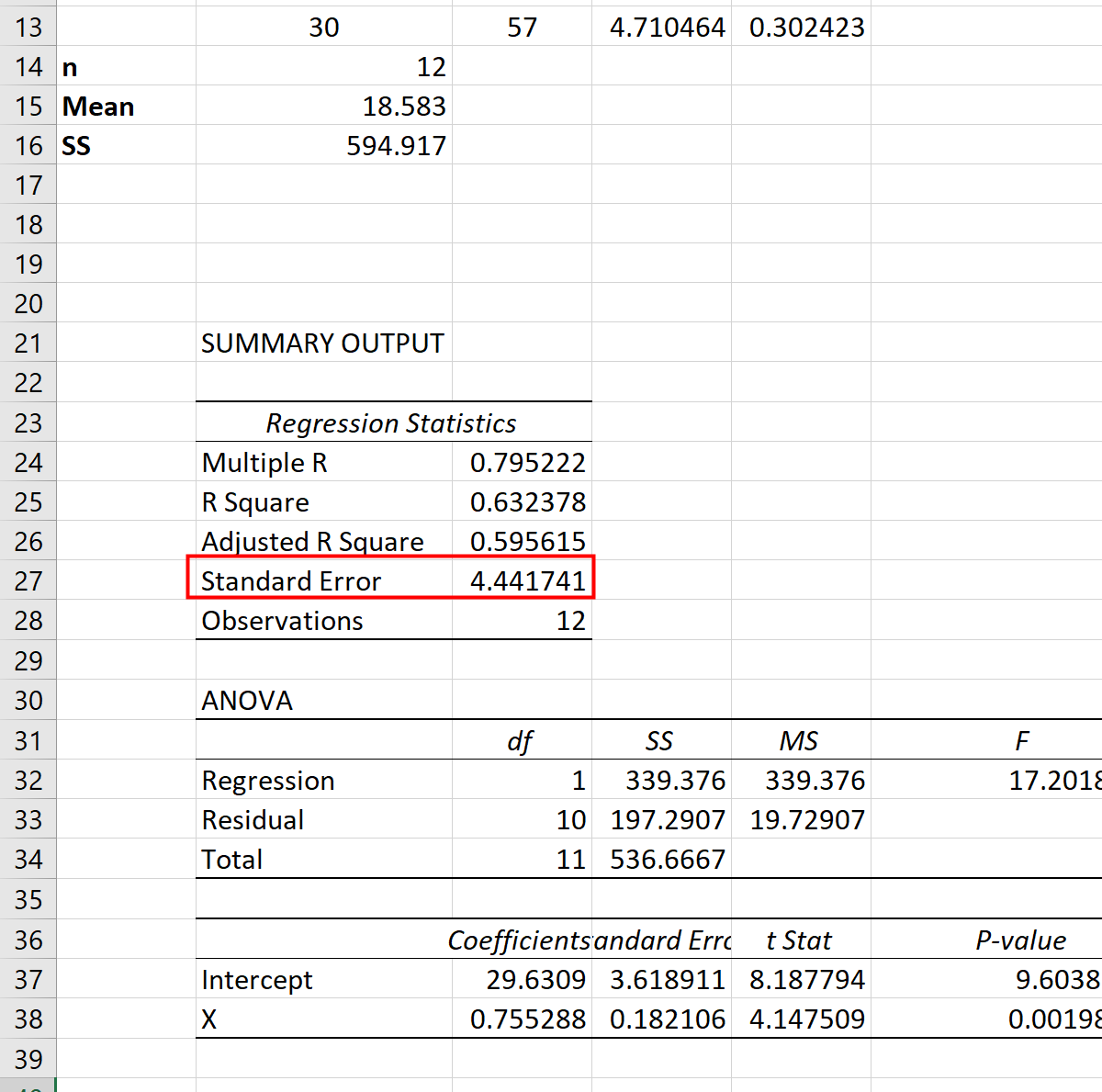
Zatem możemy użyć następującego wzoru do obliczenia reszty standaryzowanej dla każdej obserwacji:

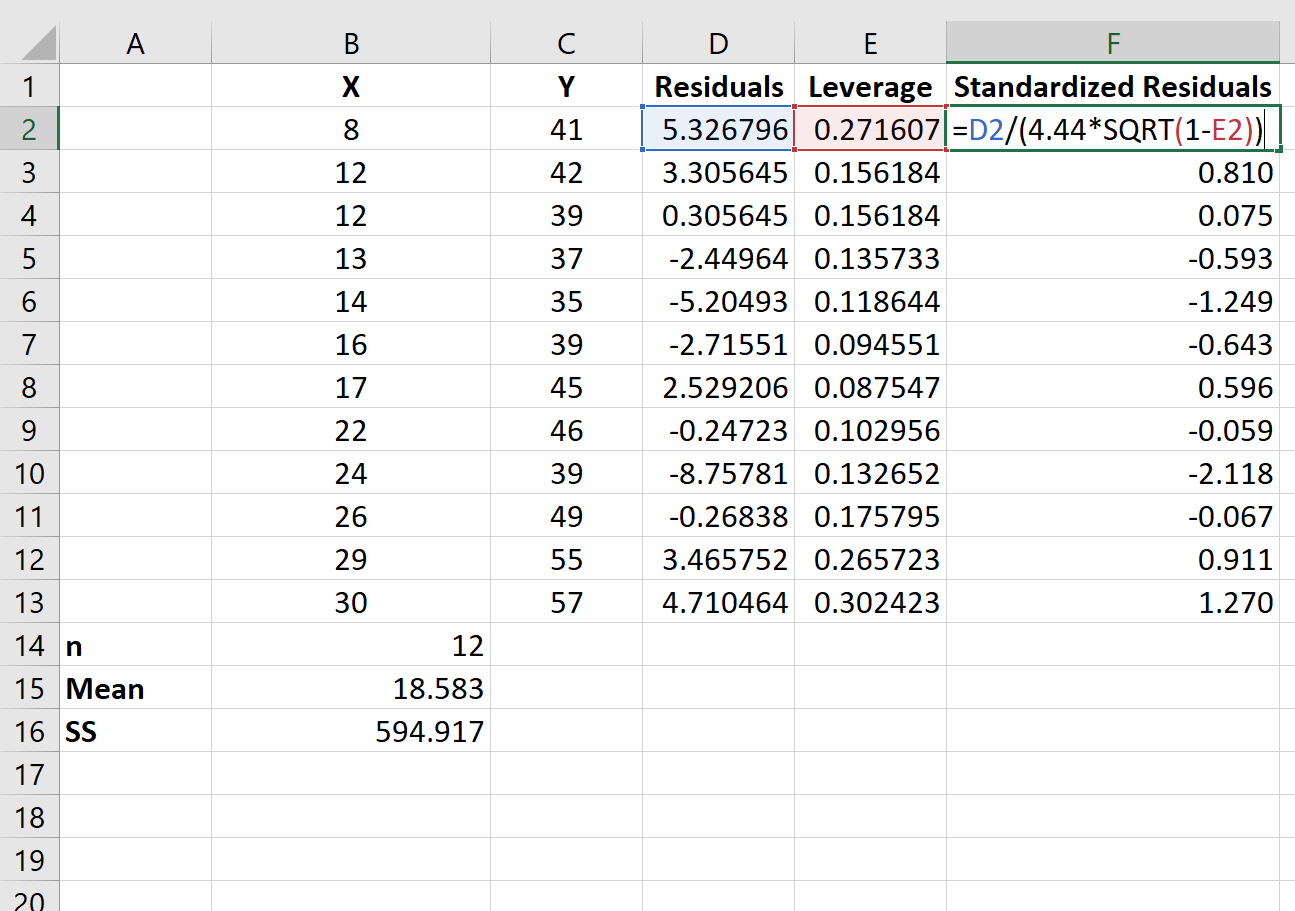
Z wyników widać, że żadna ze standaryzowanych reszt nie przekracza wartości bezwzględnej 3. Zatem żadna z obserwacji nie wydaje się być wartością odstającą.

Należy zauważyć, że w niektórych przypadkach badacze uważają obserwacje, których reszty standaryzowane przekraczają wartość bezwzględną 2, za obserwacje odstające.

To od Ciebie zależy, czy użyć wartości bezwzględnej 2 czy 3 jako progu wartości odstających, w zależności od konkretnego problemu, nad którym pracujesz.

Dodatkowe zasoby

Co to są pozostałości?
Co to są reszty standaryzowane?
Wprowadzenie do wielokrotnej regresji liniowej