Jak używać funkcji lm() w r, aby dopasować modele liniowe

Funkcja lm() w R służy do dopasowania modeli regresji liniowej.

Ta funkcja wykorzystuje następującą podstawową składnię:

lm(formuła, dane, …)

Złoto:

• formuła: Formuła modelu liniowego (np. y ~ x1 + x2)
• dane: nazwa bloku danych zawierającego dane

Poniższy przykład pokazuje, jak używać tej funkcji w R, aby wykonać następujące czynności:

• Dopasuj model regresji
• Wyświetl podsumowanie dopasowania modelu regresji
• Zobacz wykresy diagnostyczne modelu
• Narysuj dopasowany model regresji
• Dokonuj prognoz za pomocą modelu regresji

Dopasuj model regresji

Poniższy kod pokazuje, jak użyć funkcji lm() w celu dopasowania modelu regresji liniowej w R:

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

Pokaż podsumowanie modelu regresji

Możemy następnie użyć funkcji podsumowania() , aby wyświetlić podsumowanie dopasowania modelu regresji:

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

Oto jak interpretować najważniejsze wartości w modelu:

• Statystyka F = 18,35, odpowiadająca wartość p = 0,002675. Ponieważ ta wartość p jest mniejsza niż 0,05, model jako całość jest istotny statystycznie.
• Wielokrotne R do kwadratu = 0,6964. To mówi nam, że 69,64% zmienności zmiennej odpowiedzi y można wyjaśnić zmienną predykcyjną x.
• Szacowany współczynnik x : 1,2780. To mówi nam, że każda dodatkowa jednostka wzrostu x jest powiązana ze średnim wzrostem y o 1,2780.

Możemy następnie wykorzystać szacunki współczynników z wyników do napisania oszacowanego równania regresji:

y = 11,1432 + 1,2780*(x)

Bonus : kompletny przewodnik dotyczący interpretacji każdej wartości wyniku regresji w R znajdziesztutaj .

Zobacz wykresy diagnostyczne modelu

Następnie możemy użyć funkcji plot() do wykreślenia wykresów diagnostycznych modelu regresji:

 #create diagnostic plots
plot(model) 

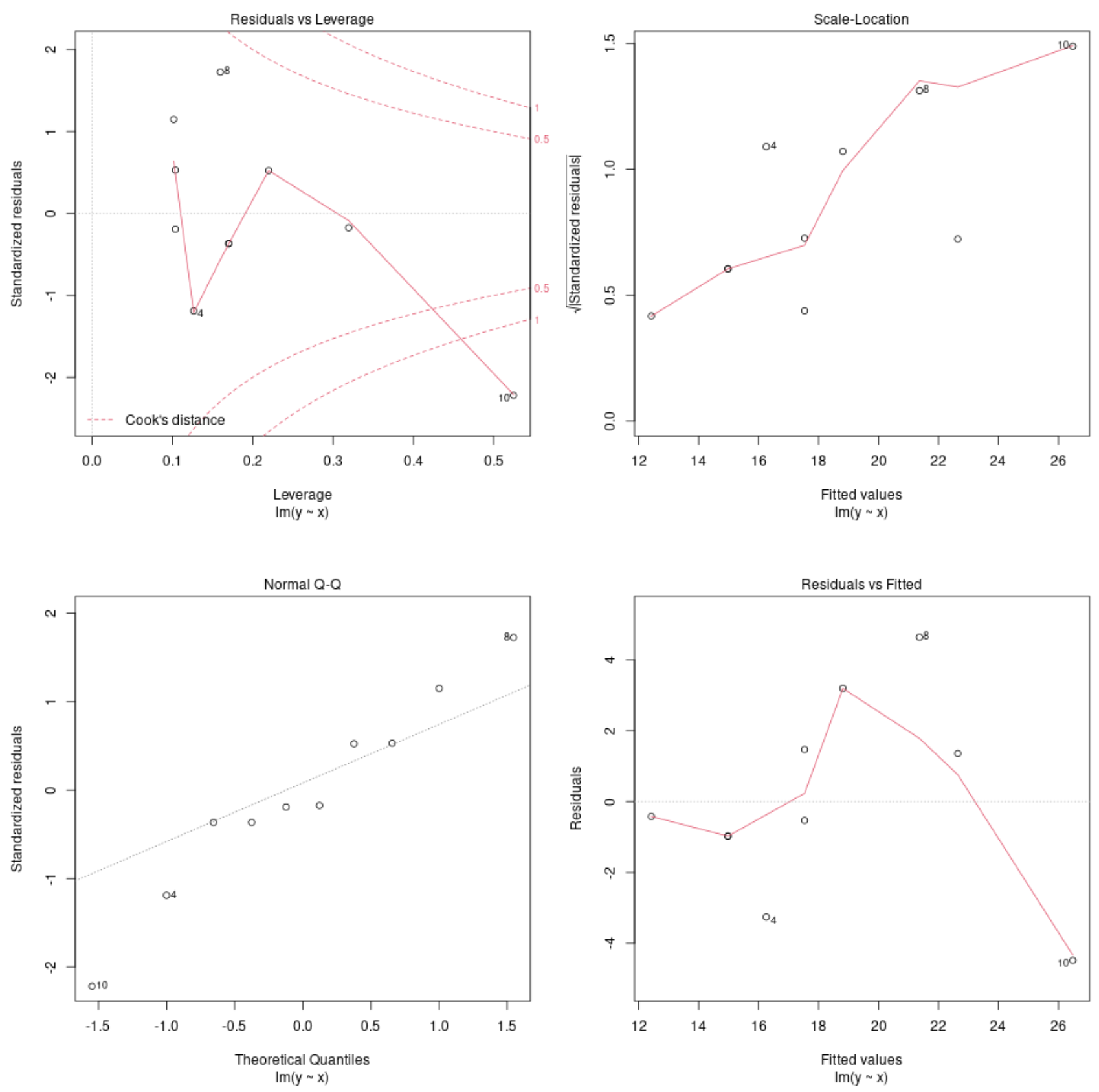
Wykresy te pozwalają nam przeanalizować reszty modelu regresji w celu ustalenia, czy model jest odpowiedni do wykorzystania w przypadku danych.

Pełne wyjaśnienie sposobu interpretacji wykresów diagnostycznych modelu w języku R można znaleźć w tym samouczku.

Narysuj dopasowany model regresji

Możemy użyć funkcji abline() do wykreślenia dopasowanego modelu regresji:

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

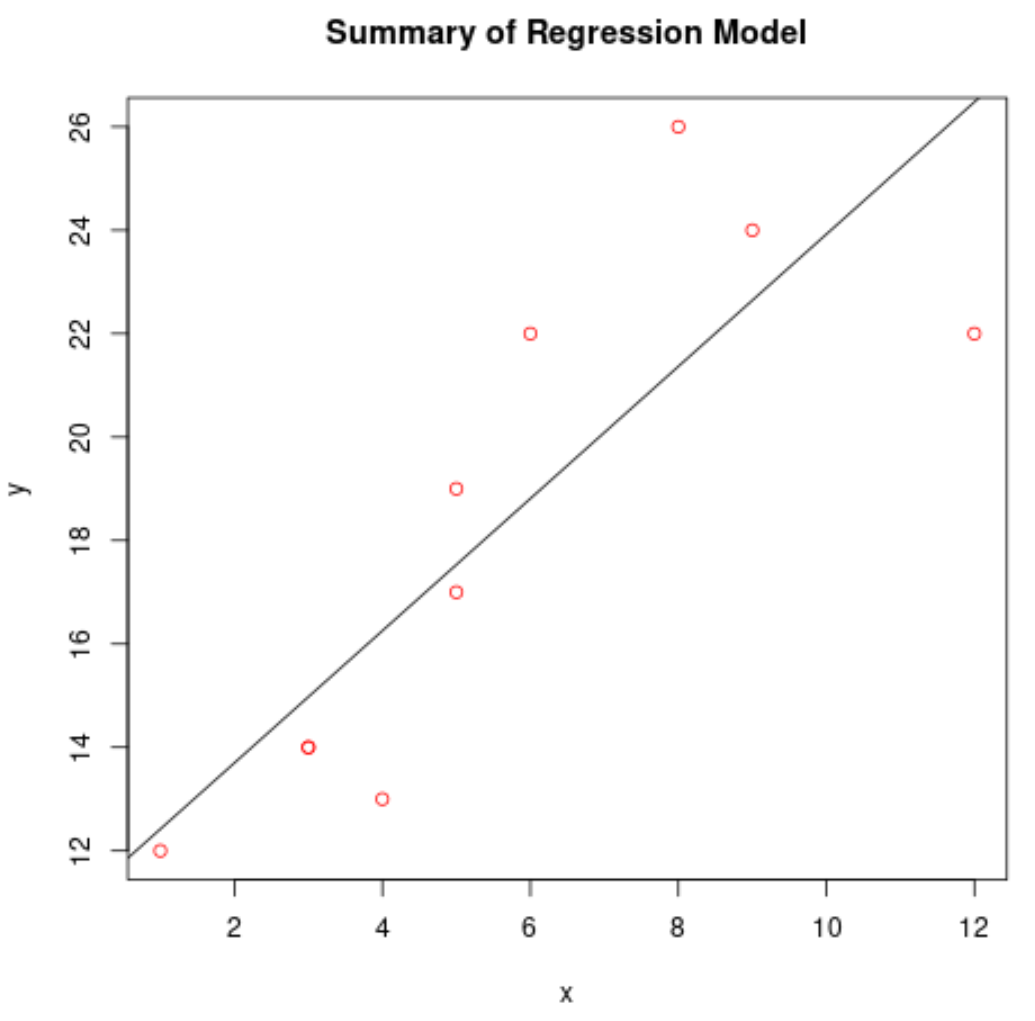
Do prognozowania użyj modelu regresji

Możemy użyć funkcji przewidywania(), aby przewidzieć wartość odpowiedzi dla nowej obserwacji:

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

Model przewiduje, że wartość odpowiedzi na tę nową obserwację wyniesie 17,5332 .

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak przeprowadzić regresję krokową w R