Funkcja prawdopodobieństwa

W tym artykule wyjaśniono, czym są funkcje prawdopodobieństwa. W ten sposób znajdziesz znaczenie funkcji prawdopodobieństwa, jej właściwości i konkretny przykład obliczenia funkcji prawdopodobieństwa. Dodatkowo przedstawiono różnice pomiędzy funkcją prawdopodobieństwa a innymi typami funkcji probabilistycznych.

Co to jest funkcja prawdopodobieństwa?

Funkcja prawdopodobieństwa , zwana także funkcją masy prawdopodobieństwa , jest funkcją matematyczną opisującą prawdopodobieństwo, że dyskretna zmienna losowa przyjmie określoną wartość.

Oznacza to, że funkcja prawdopodobieństwa zwraca prawdopodobieństwo, że powiązane ze zmienną dyskretną jest dokładnie równe wartości.

Na przykład prawdopodobieństwo wyrzucenia dowolnej liczby podczas rzutu kostką wynosi 1/6 (kość ma sześć boków), dlatego funkcja prawdopodobieństwa związana z tą przestrzenią próbek będzie równa 1/6 dla n bez względu na wartość.

Własności funkcji prawdopodobieństwa

Funkcje prawdopodobieństwa mają następujące właściwości:

• Prawdopodobieństwa nie mogą być ujemne, dlatego funkcja prawdopodobieństwa ma wartość zero lub jest dodatnia dla dowolnej wartości x.

• Podobnie maksymalne prawdopodobieństwo wynosi jedność, co oznacza, że zdarzenie zawsze nastąpi. Dlatego maksymalna wartość funkcji prawdopodobieństwa jest równa 1.

• Wreszcie suma wszystkich wartości funkcji prawdopodobieństwa daje 1, ponieważ jest to suma wszystkich prawdopodobieństw w przestrzeni próbki.

Przykład funkcji prawdopodobieństwa

Teraz, gdy znamy definicję i charakterystykę funkcji prawdopodobieństwa, zobaczmy przykład tego typu funkcji probabilistycznej.

• Oblicz prawdopodobieństwo wyrzucenia orła 0, 1, 2, 3 i 4 razy, wykonując cztery niezależne rzuty monetą. Następnie wykreśl znalezioną funkcję prawdopodobieństwa.

Przede wszystkim musimy obliczyć prawdopodobieństwo wyrzucenia orła, w tym celu musimy podzielić możliwe przypadki przez całkowitą liczbę przypadków. Obliczenia wszystkich prawdopodobieństw można zobaczyć w poniższej tabeli:

A kiedy już obliczyliśmy wszystkie prawdopodobieństwa, możemy przedstawić wartości funkcji prawdopodobieństwa na wykresie:

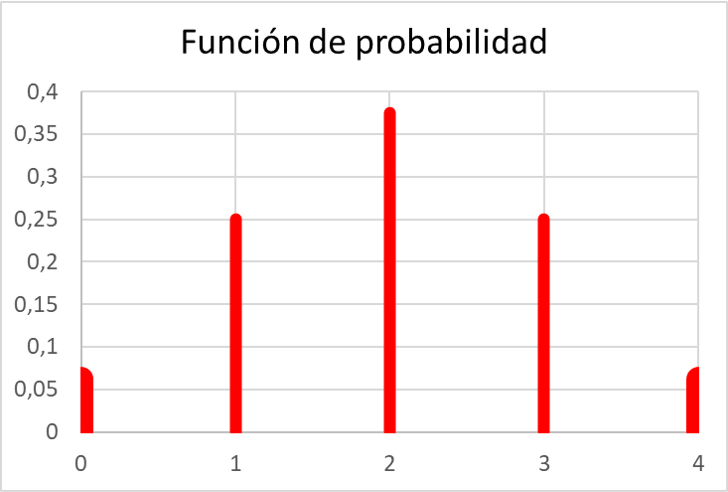
Jak widać, funkcja probabilistyczna w ćwiczeniu spełnia wszystkie właściwości funkcji prawdopodobieństwa, ponieważ wszystkie jej wartości mieszczą się w przedziale od 0 do 1, a ponadto suma wszystkich jej wartości jest równa 1.

Funkcja prawdopodobieństwa i funkcja gęstości

W tej sekcji zobaczymy różnicę między funkcją prawdopodobieństwa a funkcją gęstości, ponieważ są to dwa rodzaje funkcji probabilistycznych, które mają ten sam cel, ale są używane w różnych przypadkach.

Różnica między funkcją prawdopodobieństwa a funkcją gęstości to rodzaj zmiennej, dla której opisują prawdopodobieństwa. Funkcja prawdopodobieństwa służy do określenia prawdopodobieństw zmiennej dyskretnej, natomiast funkcja gęstości służy do określenia prawdopodobieństw zmiennej ciągłej.

Zatem w zależności od zmiennej używana jest funkcja prawdopodobieństwa lub funkcja gęstości.

Aby dowiedzieć się więcej o funkcji gęstości, kliknij poniższy link:

Funkcja prawdopodobieństwa i funkcja rozkładu

Różnica między funkcją prawdopodobieństwa a funkcją rozkładu polega na rodzaju definiowanego przez nie prawdopodobieństwa. Funkcja prawdopodobieństwa wskazuje prawdopodobieństwo, że zmienna przyjmie określoną wartość, natomiast funkcja rozkładu opisuje skumulowane prawdopodobieństwo zmiennej.

Dlatego dystrybuantę oblicza się z funkcji prawdopodobieństwa.

Jako przykład, w poniższym linku możesz zobaczyć obliczenie funkcji rozkładu pozwalającej uzyskać orła w czterech rzutach monetą, w oparciu o funkcję prawdopodobieństwa przedstawioną w powyższym ćwiczeniu.