Zrozumienie hipotezy zerowej dla modeli anova

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej niezależnych grup.

Jednoczynnikowa ANOVA wykorzystuje następujące hipotezy zerowe i alternatywne:

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (wszystkie średnie grupowe są równe)
• H _A : Co najmniej jedna średnia grupowa jest inna   odpoczynek

Aby zdecydować, czy powinniśmy odrzucić hipotezę zerową, czy nie, musimy odnieść się do wartości p w wyniku tabeli ANOVA.

Jeśli wartość p jest poniżej pewnego poziomu istotności (np. 0,05), wówczas możemy odrzucić hipotezę zerową i stwierdzić, że nie wszystkie średnie grupowe są równe.

Dwuczynnikową analizę ANOVA stosuje się w celu ustalenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub większej liczby niezależnych grup przypisanych do dwóch zmiennych (czasami nazywanych „czynnikami”).

Dwukierunkowa ANOVA testuje jednocześnie trzy hipotezy zerowe:

• Wszystkie średnie grupowe są równe na każdym poziomie pierwszej zmiennej
• Wszystkie średnie grupowe są równe na każdym poziomie drugiej zmiennej
• Nie ma efektu interakcji pomiędzy tymi dwiema zmiennymi

Aby zdecydować, czy powinniśmy odrzucić każdą hipotezę zerową, musimy odwołać się do wartości p w wyniku dwuczynnikowej tabeli ANOVA.

Poniższe przykłady pokazują, jak zdecydować, czy odrzucić hipotezę zerową w jednokierunkowej ANOVA i dwukierunkowej ANOVA.

Przykład 1: Jednokierunkowa ANOVA

Załóżmy, że chcemy wiedzieć, czy trzy różne programy przygotowujące do testów prowadzą do różnych średnich wyników na danym egzaminie. Aby to przetestować, rekrutujemy 30 studentów do udziału w badaniu i dzielimy ich na trzy grupy.

Uczniowie w każdej grupie są losowo przydzielani do korzystania z jednego z trzech programów przygotowujących do testów przez kolejne trzy tygodnie w celu przygotowania się do egzaminu. Po trzech tygodniach wszyscy uczniowie przystępują do tego samego egzaminu.

Poniżej wyniki egzaminów dla poszczególnych grup:

Kiedy wprowadzimy te wartości do jednokierunkowego kalkulatora ANOVA , jako wynik otrzymamy następującą tabelę ANOVA:

Należy zauważyć, że wartość p wynosi 0,11385 .

W tym konkretnym przykładzie użylibyśmy następujących hipotez zerowych i alternatywnych:

• H ₀ : μ ₁ = μ ₂ = μ ₃ (średni wynik egzaminu dla każdej grupy jest równy)
• H _A : Co najmniej jedna średnia grupowa jest inna   odpoczynek

Ponieważ wartość p tabeli ANOVA jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje statystycznie istotna różnica pomiędzy średnimi wynikami egzaminów trzech grup.

Przykład 2: Dwukierunkowa ANOVA

Załóżmy, że botanik chce wiedzieć, czy na wzrost roślin wpływa ekspozycja na światło słoneczne i częstotliwość podlewania.

Sadzi 40 nasion i pozwala im rosnąć przez dwa miesiące w różnych warunkach nasłonecznienia i częstotliwości podlewania. Po dwóch miesiącach rejestruje wysokość każdej rośliny. Wyniki przedstawiono poniżej:

W powyższej tabeli widzimy, że w każdej kombinacji warunków hodowano pięć roślin.

Na przykład pięć roślin uprawiano przy codziennym podlewaniu i bez światła słonecznego, a ich wysokość po dwóch miesiącach wynosiła 4,8 cala, 4,4 cala, 3,2 cala, 3,9 cala i 4,4 cala:

Wykonuje dwuczynnikową analizę ANOVA w Excelu i otrzymuje następujący wynik:

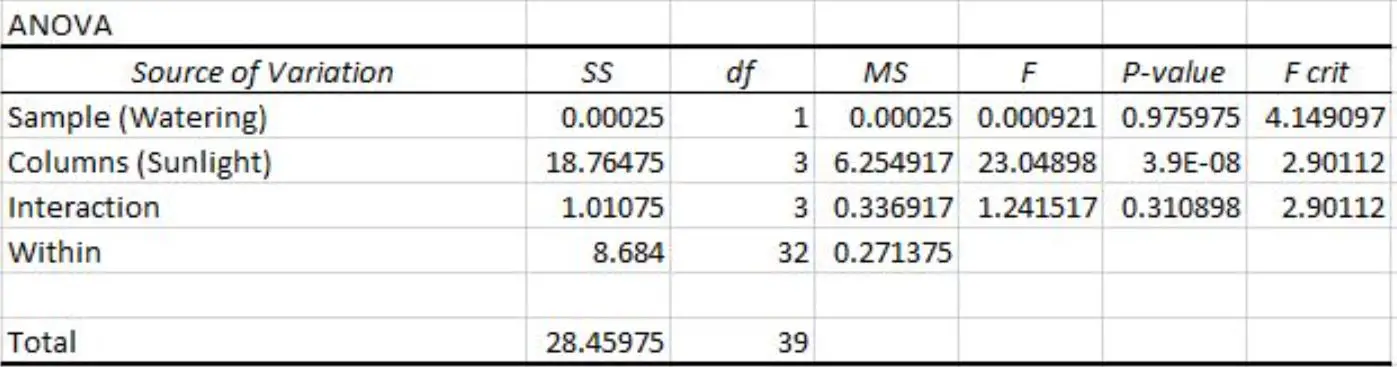
W wyniku dwuczynnikowej tabeli ANOVA możemy zobaczyć następujące wartości p:

• Wartość p dla częstotliwości nawadniania wynosi 0,975975 . Nie jest to istotne statystycznie na poziomie istotności 0,05.
• Wartość p dla ekspozycji na słońce wynosi 3,9E-8 (0,000000039) . Jest to statystycznie istotne na poziomie istotności 0,05.
• Wartość p dla interakcji pomiędzy częstotliwością podlewania a ekspozycją na słońce wynosi 0,310898 . Nie jest to istotne statystycznie na poziomie istotności 0,05.

Wyniki te wskazują, że ekspozycja na słońce jest jedynym czynnikiem mającym statystycznie istotny wpływ na wysokość roślin.

A ponieważ nie ma efektu interakcji, wpływ ekspozycji na słońce jest stały na każdym poziomie częstotliwości podlewania.

Mówiąc najprościej, to, czy roślina jest podlewana codziennie, czy co tydzień, nie ma wpływu na wpływ ekspozycji na słońce na roślinę.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji o modelach ANOVA:

Jak interpretować wartość F i wartość P w ANOVA
Jak obliczyć sumę kwadratów w ANOVA
Co oznacza wysoka wartość F w ANOVA?