Trzy hipotezy sformułowane w teście t dla par
Test t dla par prób służy do porównania średnich z dwóch próbek, gdy każdą obserwację w jednej próbie można powiązać z obserwacją w drugiej próbie.
Ten typ testu przyjmuje następujące założenia dotyczące danych:
1. Niezależność: każda obserwacja musi być niezależna od jakiejkolwiek innej obserwacji.
2. Normalność: Różnice między parami powinny mieć w przybliżeniu rozkład normalny.
3. Brak skrajnych wartości odstających: w różnicach nie powinny występować skrajne wartości odstające.
Jeżeli jedno lub więcej z tych założeń nie zostanie spełnione, wyniki testu t dla par próbek mogą być niewiarygodne lub wprowadzające w błąd.
W tym samouczku wyjaśniamy każde założenie, jak ustalić, czy założenie jest spełnione i co zrobić, jeśli zostanie naruszone.
Hipoteza 1: Niepodległość
Test t dla par próbek zakłada, że każda obserwacja jest niezależna od wszystkich innych obserwacji.
Jak zweryfikować tę hipotezę
Najprostszym sposobem sprawdzenia tego założenia jest sprawdzenie, czy każdą obserwację zebrano metodą losowego doboru próby .
Jeżeli zastosowano metodę doboru losowego (np. dobór losowy prosty), to możemy założyć, że każda obserwacja jest niezależna od wszystkich innych obserwacji.
Co zrobić, jeśli to założenie nie jest przestrzegane
Jeżeli to założenie nie jest spełnione, wyniki testu t dla par próbek są całkowicie nieważne.
W tym scenariuszu najlepiej jest zebrać nowe obserwacje, stosując metodę losowego doboru próby, aby zapewnić niezależność każdej obserwacji.
Hipoteza 2: normalność
Test t dla par próbek zakłada, że różnice między parami powinny mieć w przybliżeniu rozkład normalny.
Jest to kluczowe założenie, ponieważ jeśli różnice między parami nie mają rozkładu normalnego, nie można wyciągać wniosków na podstawie wartości p testu.
Jak zweryfikować tę hipotezę
Najprostszym sposobem sprawdzenia tej hipotezy jest po prostu utworzenie histogramu różnic w parach i wizualne sprawdzenie, czy histogram ma kształt dzwonu.
Na przykład, jeśli histogram wygląda tak, powiedzielibyśmy, że założenie normalności jest spełnione:
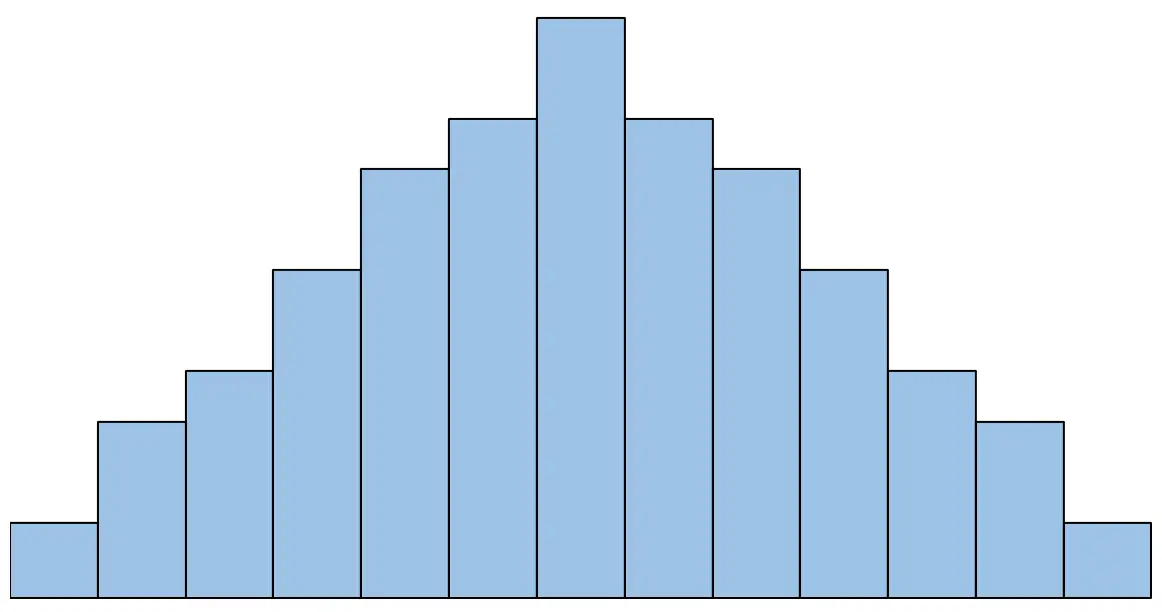
Jeśli jednak histogram wygląda tak, powiedzielibyśmy, że założenie normalności nie jest spełnione:
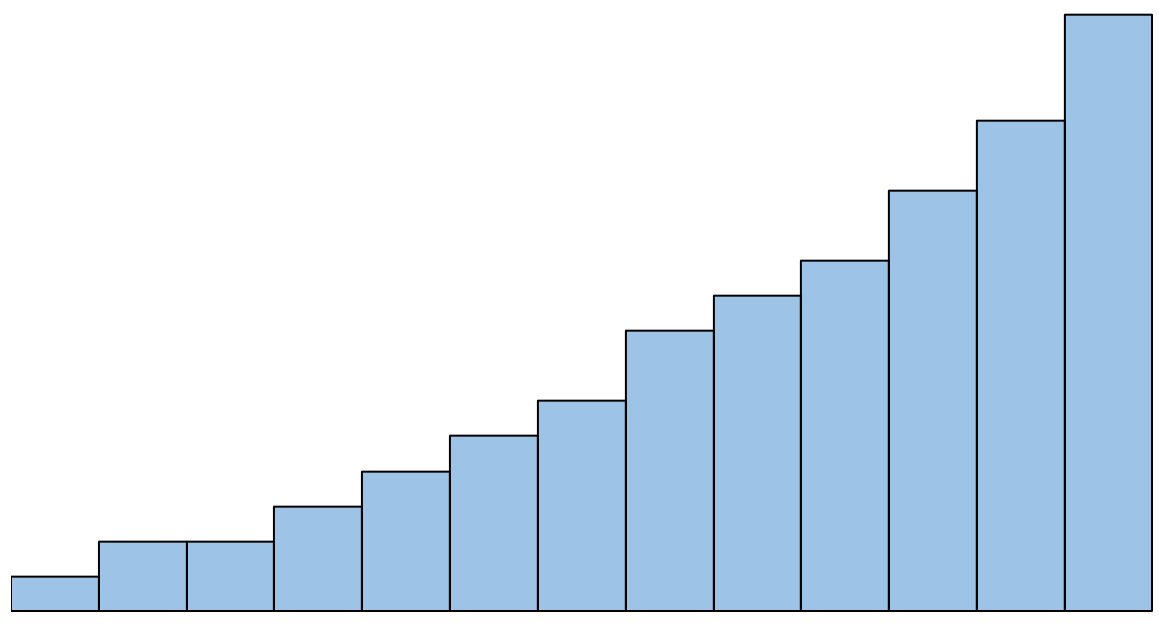
Co zrobić, jeśli to założenie nie jest przestrzegane
Jeżeli to założenie zostanie naruszone, możemy wykonać test rang ze znakiem Wilcoxona , który jest uważany za nieparametryczny odpowiednik testu t dla par próbek i nie zakłada, że różnice w parach mają rozkład normalny.
Hipoteza 3: brak skrajnych wartości odstających
Test t dla par prób zakłada, że w danych nie ma skrajnych wartości odstających.
Jak zweryfikować tę hipotezę
Najłatwiejszym sposobem przetestowania tej hipotezy jest utworzenie wykresu pudełkowego par różnic i wizualne sprawdzenie, czy istnieją jakieś wartości odstające.
Załóżmy na przykład, że wykres pudełkowy różnic w parach wygląda następująco:
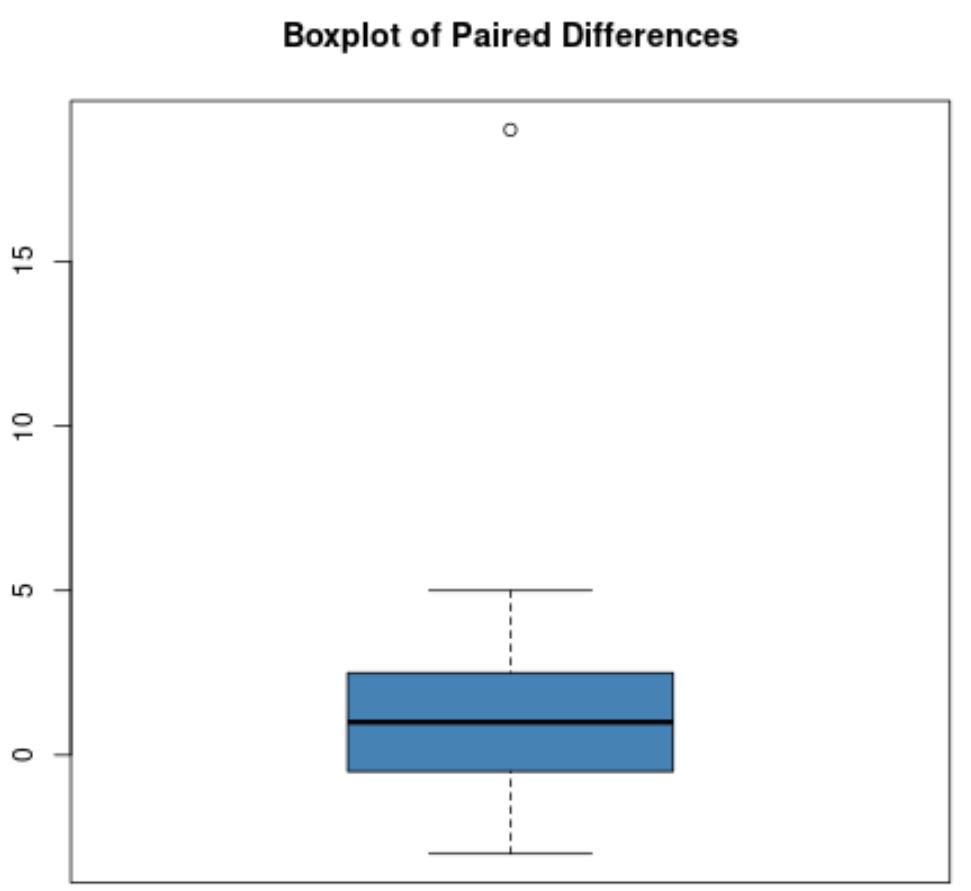
Większość różnic w parach jest bliska zeru, ale istnieje jedna różnica w parach równa około 19, co jest wyraźnie wartością odstającą.
Uwaga : Na wykresie pudełkowym zwykle stosuje się okrąg, aby wskazać wartość odstającą.
Załóżmy jednak, że wykres pudełkowy różnic w parach wygląda następująco:
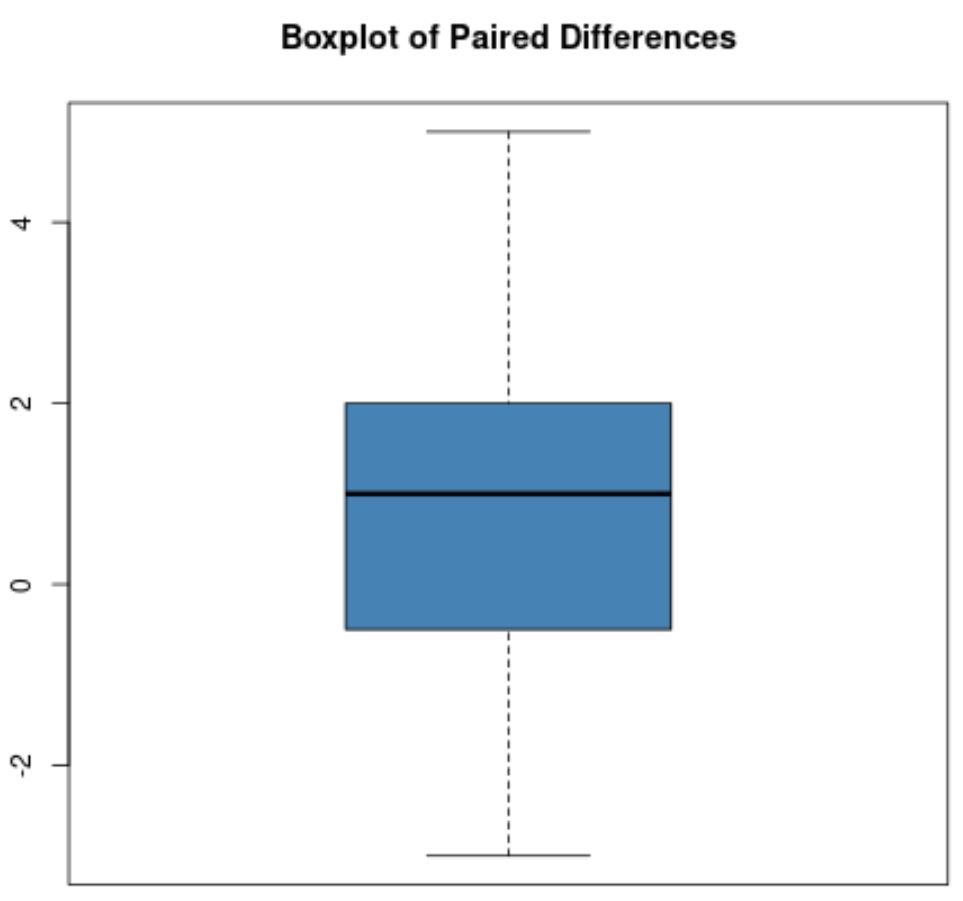
Na tym wykresie pudełkowym nie ma wyraźnych wartości odstających, więc założymy, że w danych nie ma żadnych skrajnych wartości odstających.
Co zrobić, jeśli to założenie nie jest przestrzegane
Jeśli to założenie zostanie naruszone, wartość odstająca może nieprawidłowo wpłynąć na wyniki testu t dla par próbek.
W tym scenariuszu można usunąć wartość odstającą, jeśli uważasz, że reprezentuje ona błędny punkt danych lub jest wynikiem błędu we wprowadzaniu danych.
Alternatywnie możesz zachować wartość odstającą i po prostu zanotować ją podczas raportowania wyników testu t dla prób zależnych.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają założenia przyjęte w innych testach statystycznych:
Cztery hipotezy sformułowane w teście t
Cztery hipotezy testu chi-kwadrat
Cztery hipotezy testów parametrycznych