Jak utworzyć histogram reszt w r

Jednym z głównych założeń regresji liniowej jest to, że reszty mają rozkład normalny.

Jednym ze sposobów wizualnej weryfikacji tego założenia jest utworzenie histogramu reszt i obserwacja, czy rozkład ma kształt dzwonu przypominający rozkład normalny .

W tym samouczku przedstawiono krok po kroku przykład tworzenia histogramu reszt dla modelu regresji w języku R.

Krok 1: Utwórz dane

Najpierw utwórzmy fałszywe dane do pracy:

 #make this example reproducible
set.seed(0)

#createdata
x1 <- rnorm(n=100, 2, 1)
x2 <- rnorm(100, 4, 3)
y <- rnorm(100, 2, 3)
data <- data.frame(x1, x2, y)

#view first six rows of data
head(data)

        x1 x2 y
1 3.262954 6.3455776 -1.1371530
2 1.673767 1.6696701 -0.6886338
3 3.329799 2.1520303 5.8081615
4 3.272429 4.1397409 3.7815228
5 2.414641 0.6088427 4.3269030
6 0.460050 5.7301563 6.6721111

Krok 2: Dopasuj model regresji

Następnie dopasujemy do danych model wielokrotnej regresji liniowej :

 #fit multiple linear regression model
model <- lm(y ~ x1 + x2, data=data)

Krok 3: Utwórz histogram reszt

Na koniec użyjemy pakietu wizualizacji ggplot do stworzenia histogramu reszt modelu:

 #load ggplot2
library (ggplot2)

#create histogram of residuals
ggplot(data = data, aes (x = model$residuals)) +
    geom_histogram(fill = ' steelblue ', color = ' black ') +
    labs(title = ' Histogram of Residuals ', x = ' Residuals ', y = ' Frequency ')

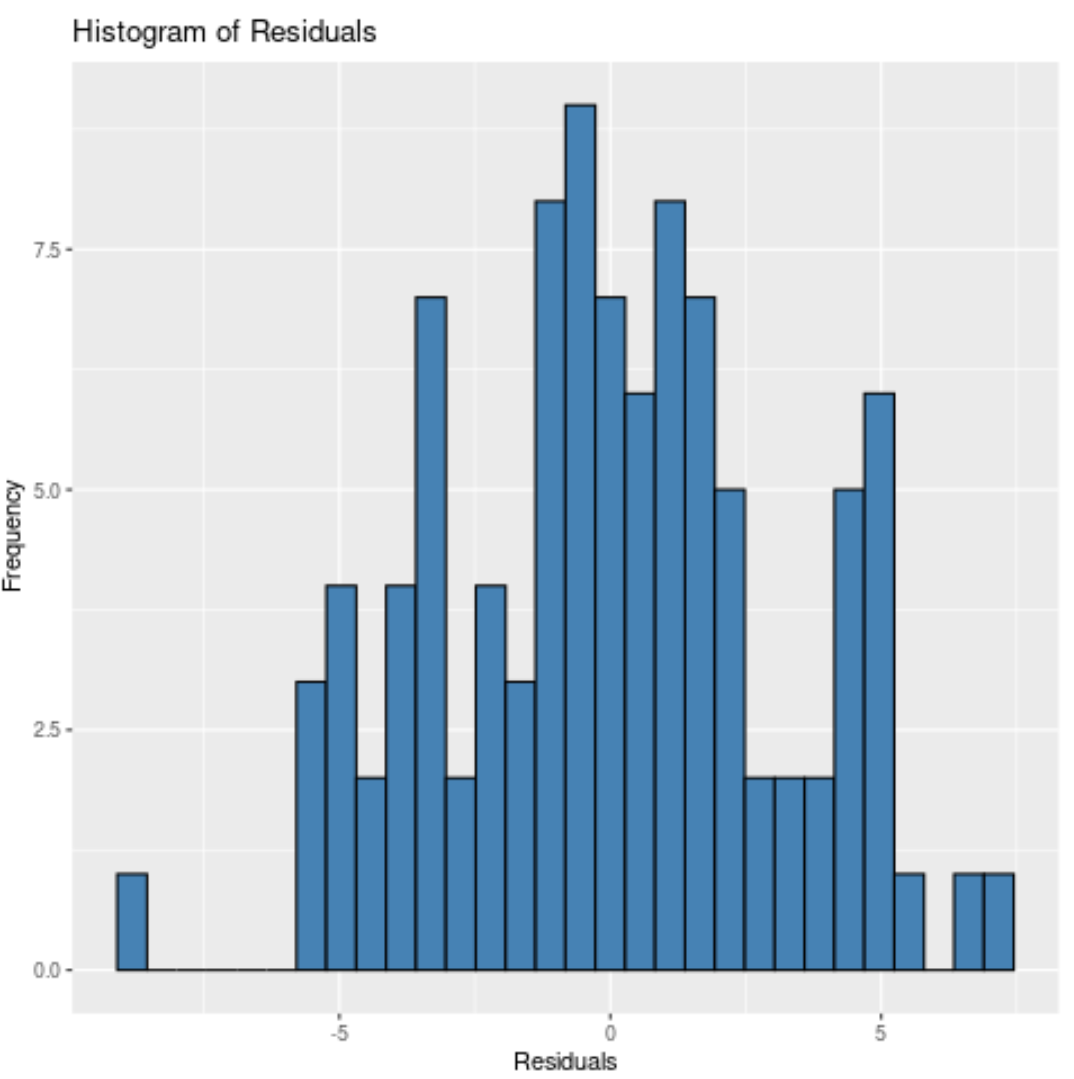
Zauważ, że możemy również określić liczbę pojemników, w których należy umieścić pozostałości, używając argumentu bin .

Im mniej pól, tym szersze słupki będą na histogramie. Na przykład możemy określić 20 pojemników :

 #create histogram of residuals
ggplot(data = data, aes (x = model$residuals)) +
    geom_histogram(bins = 20 , fill = ' steelblue ', color = ' black ') +
    labs(title = ' Histogram of Residuals ', x = ' Residuals ', y = ' Frequency ') 

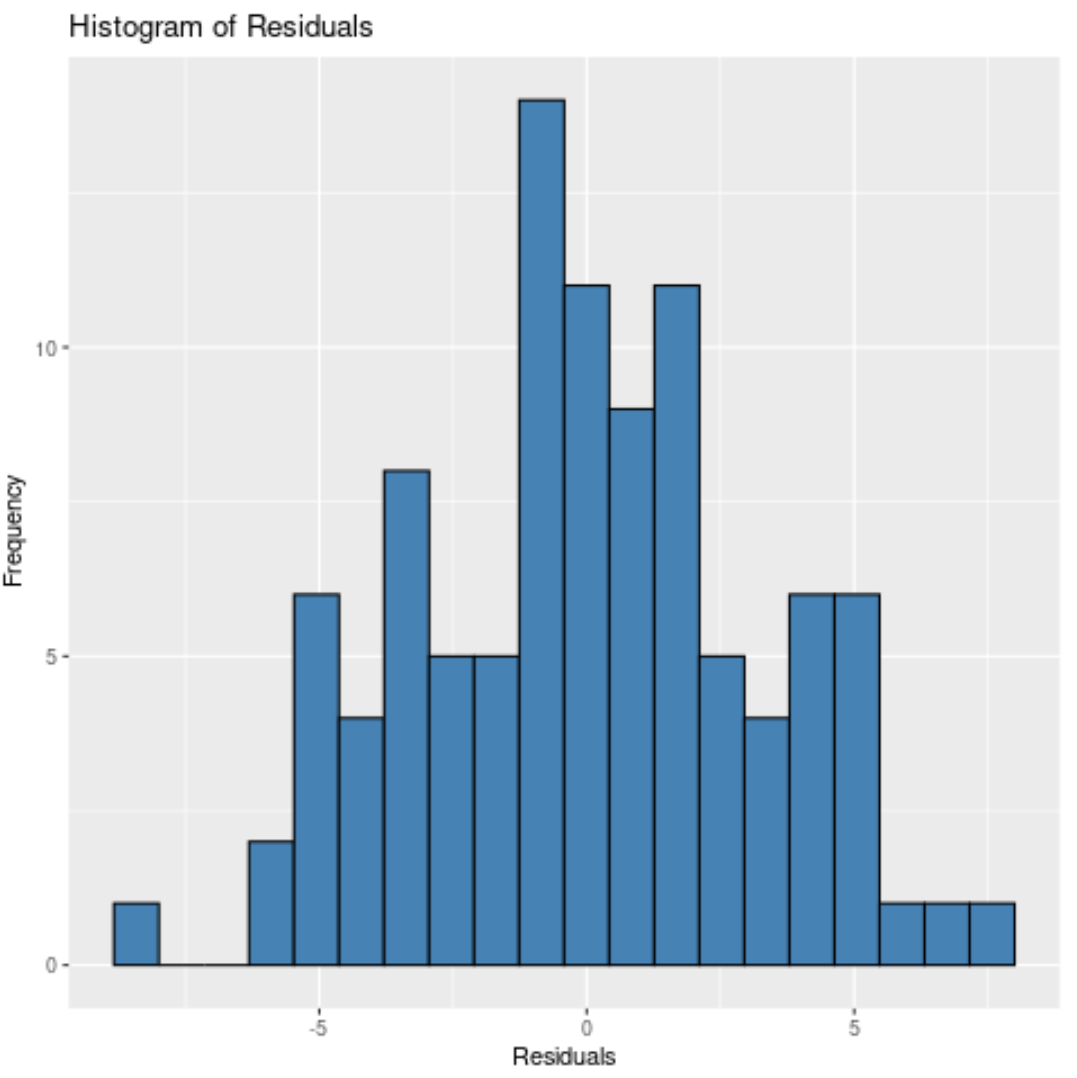
Lub moglibyśmy określić 10 pojemników :

 #create histogram of residuals
ggplot(data = data, aes (x = model$residuals)) +
    geom_histogram(bins = 10 , fill = ' steelblue ', color = ' black ') +
    labs(title = ' Histogram of Residuals ', x = ' Residuals ', y = ' Frequency ') 

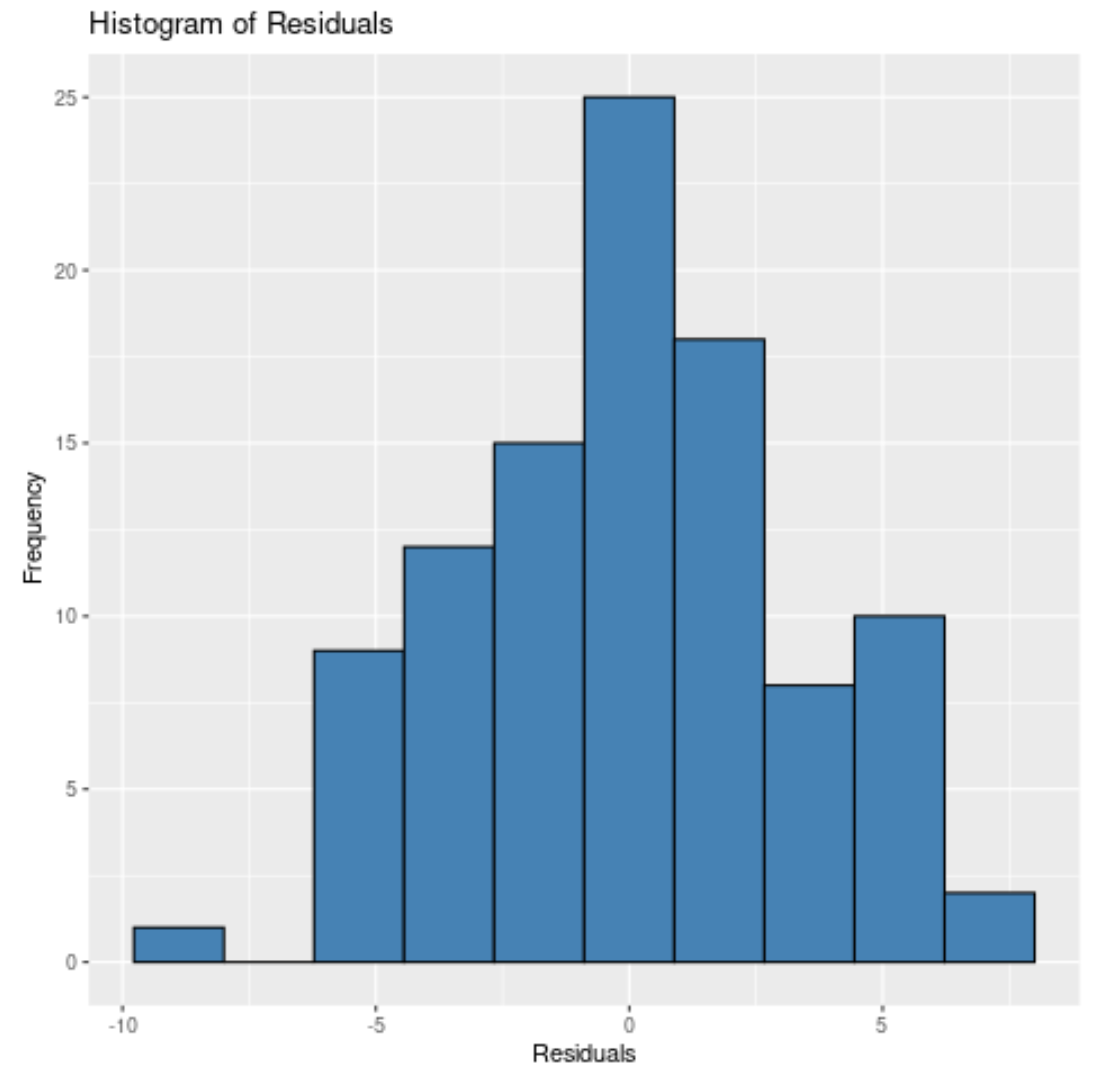
Bez względu na to, ile pudełek określimy, możemy zobaczyć, że reszty mają w przybliżeniu rozkład normalny.

Moglibyśmy również przeprowadzić formalny test statystyczny, taki jak Shapiro-Wilk, Kołmogorow-Smirnow lub Jarque-Bera, aby sprawdzić normalność.

Należy jednak pamiętać, że testy te są wrażliwe na duże próbki – to znaczy często wyciągają wniosek, że reszty nie są normalne, gdy wielkość próbki jest duża.

Z tego powodu często łatwiej jest ocenić normalność, tworząc histogram reszt.