Indeks giniego (lub współczynnik giniego)

Przez Benjamin Anderson 5 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest wskaźnik Giniego, zwany także współczynnikiem Giniego i do czego służy. Dodatkowo znajdziesz rozwiązane ćwiczenie dotyczące znajdowania indeksu Giniego. Wreszcie będziesz mógł zobaczyć interpretację tej metryki statystycznej i jaka jest zależność między indeksem Giniego a krzywą Lorenza.

Co to jest indeks Giniego?

Indeks Giniego , zwany także współczynnikiem Giniego , jest wartością statystyczną stosowaną do pomiaru nierówności dochodów na danym terytorium. Innymi słowy, indeks Giniego wskazuje, jak równe jest terytorium w podziale dochodów wśród jego ludności.

Wskaźnik Giniego to liczba z zakresu od 0 do 1. Jeśli wskaźnik Giniego wynosi 0, oznacza to, że podział dochodów na danym terytorium jest możliwie sprawiedliwy (idealna równość), czyli innymi słowy, wszyscy mieszkańcy mają takie same dochody. Z drugiej strony, gdy współczynnik Giniego wynosi 1, odpowiada to doskonałej nierówności, to znaczy, że jedna osoba ma cały dochód na danym terytorium, a pozostali nie otrzymują nic.

Indeks Giniego służy do porównywania sytuacji gospodarczej różnych krajów świata, ponieważ umożliwia porównanie krajów najbardziej egalitarnych i odwrotnie, krajów najbardziej nierównych pod względem podziału dochodów.

Indeks Giniego został wynaleziony przez słynnego statystyka Corrado Giniego, stąd jego nazwa.

Jak obliczyć indeks Giniego

Biorąc pod uwagę definicję wskaźnika Giniego (lub współczynnika Giniego), oto sposób obliczania tej miary statystycznej.

Wzór na indeks Giniego (lub współczynnik Giniego) jest następujący:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-\sum_{k=1}^{n-1}(X_{k+1}-X_k)\cdot (Y_{k+1}+Y_k)\end{vmatrix}$

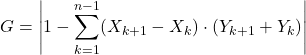
Złoto:

$G$

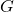
jest indeksem Giniego.
$X$

jest skumulowanym odsetkiem populacji zmiennej.
$Y$

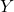
jest skumulowaną częścią zmiennej dochodu.

Abyście mogli dokładnie zobaczyć jak wyznaczany jest indeks Giniego, poniżej rozwiązano przykład krok po kroku:

Oblicz wskaźnik Giniego populacji, której dochody przedstawiono w poniższej tabeli.

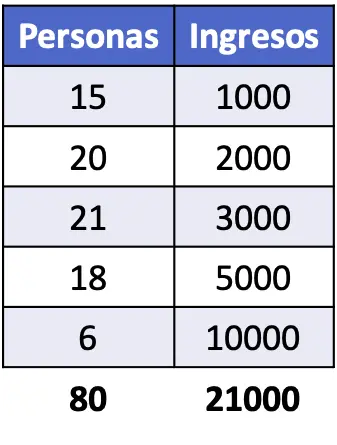
Aby znaleźć współczynnik Giniego, musimy określić proporcję każdego poziomu dochodu, a także proporcję skumulowaną. Dodatkowo należy wykonać obliczenia podane we wzorze, aby znaleźć wartość wskaźnika Giniego.

W skrócie do tabeli danych należy dodać następujące kolumny:

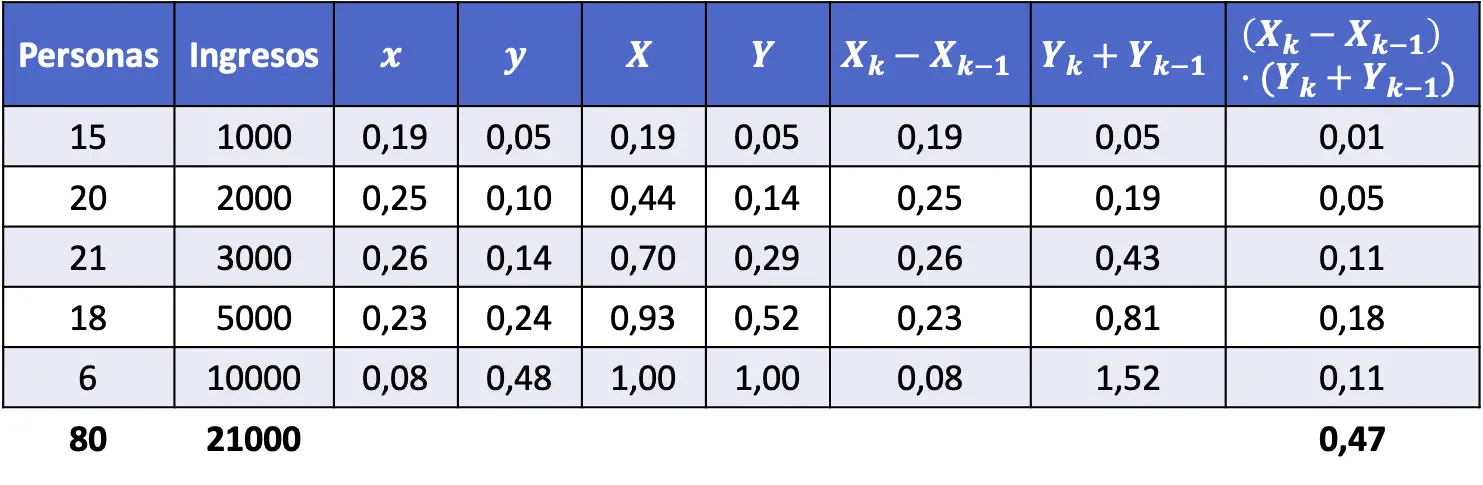
Korzystamy teraz ze wzoru na indeks Giniego:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-\sum_{k=1}^{n-1}(X_{k+1}-X_k)\cdot (Y_{k+1}+Y_k)\end{vmatrix}$

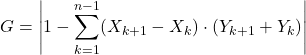
Na koniec podstawiamy dane do wyrażenia algebraicznego i obliczamy współczynnik Giniego:

$\displaystyle G=\begin{vmatrix}\displaystyle 1-0,47\end{vmatrix}=0,53$

Zależność wskaźnika Giniego od krzywej Lorenza

W tej sekcji zobaczymy, jak indeks Giniego, znany również jako współczynnik Giniego, i krzywa Lorenza są ze sobą powiązane.

Krzywa Lorenza to graficzne przedstawienie nierówności ekonomicznych ludności danego terytorium. Zatem krzywa Lorenza wizualnie wskazuje nierówność ekonomiczną populacji.

Z drugiej strony, jak widzieliśmy, wskaźnik Giniego jest wartością używaną do numerycznego opisu nierówności populacji.

Wskaźnik Giniego i krzywa Lorenza mają zatem ten sam cel : oba służą do określenia nierówności ekonomicznych pomiędzy mieszkańcami danego terytorium. Jednak indeks Giniego ocenia nierówności dochodów liczbowo, podczas gdy krzywa Lorenza analizuje graficznie nierówności ekonomiczne.

Dodatkowo wskaźnik Giniego można obliczyć z obszarów ograniczonych krzywą Lorenza według następującego wzoru:

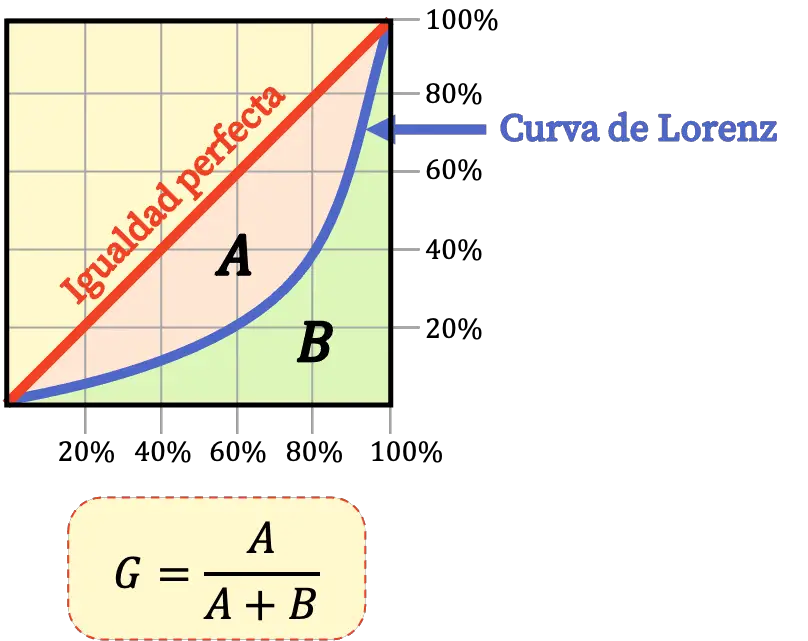
związek między indeksem Giniego a krzywą Lorenza

Interpretacja wskaźnika Giniego

Wartość indeksu Giniego może wynosić od 0 do 1 włącznie. Im wartość współczynnika Giniego jest bliższa 0, oznacza to, że na danym terytorium panuje większa równość ekonomiczna. Z drugiej strony, im wyższa wartość wskaźnika Giniego, tym większa jest nierówność w podziale dochodów pomiędzy mieszkańcami danego terytorium.

Wskaźnik Giniego będzie zatem równy zero w optymalnej sytuacji, gdy wszyscy mieszkańcy będą mieli dokładnie takie same dochody. Wręcz przeciwnie, wskaźnik Giniego będzie miał wartość 1, gdy na terytorium występuje doskonała nierówność, to znaczy, że jeden mieszkaniec otrzymuje cały dochód, a pozostali mieszkańcy nie mają żadnych dochodów.

Zatem kraje o większej równości dochodów to te z niższym indeksem Giniego. A kraje najbardziej nierównościowe mają bardzo wysoki wskaźnik Giniego.

Jak widzieliśmy, indeks Giniego jest powiązany z krzywą Lorenza. Zatem im niższy wskaźnik Giniego, tym krzywa Lorenza będzie bliżej linii doskonałej równości. Im wyższy wskaźnik Giniego, tym bardziej krzywizna będzie miała krzywa Giniego, a zatem tym dalej będzie ona od linii reprezentującej doskonałą równość.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej