Jak czytać macierz korelacji
W statystyce często staramy się zrozumieć związek między dwiema zmiennymi.
Na przykład możemy chcieć zrozumieć związek między liczbą godzin nauki studenta a oceną, jaką otrzymuje na egzaminie.
Jednym ze sposobów ilościowego określenia tej zależności jest użycie współczynnika korelacji Pearsona , który jest miarą liniowego związku między dwiema zmiennymi . Ma wartość od -1 do 1, gdzie:
- -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
- Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
- 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi
Im współczynnik korelacji jest bardziej od zera, tym silniejszy jest związek między obiema zmiennymi.
Powiązane: Co uważa się za „silną” korelację?
Jednak w niektórych przypadkach chcemy zrozumieć korelację między wieloma parami zmiennych. W takich przypadkach możemy utworzyć macierz korelacji , czyli kwadratową tabelę pokazującą współczynniki korelacji pomiędzy kilkoma zmiennymi.
Przykład macierzy korelacji
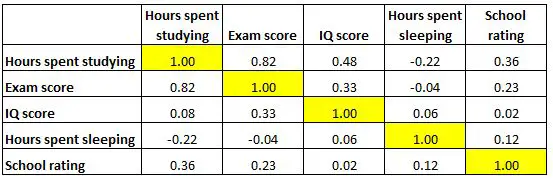
Poniższa macierz korelacji przedstawia współczynniki korelacji pomiędzy kilkoma zmiennymi związanymi z edukacją:
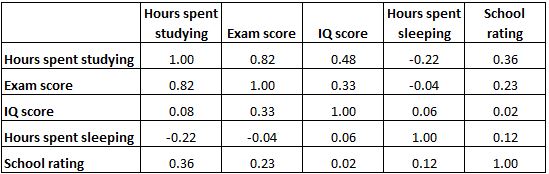
Każda komórka w tabeli pokazuje korelację pomiędzy dwiema określonymi zmiennymi. Na przykład podświetlona komórka poniżej pokazuje, że korelacja między „godzinami spędzonymi na nauce” a „oceną z egzaminu” wynosi 0,82 , co wskazuje, że są one silnie dodatnio skorelowane. Więcej godzin spędzonych na nauce jest ściśle powiązane z wyższymi wynikami egzaminów.
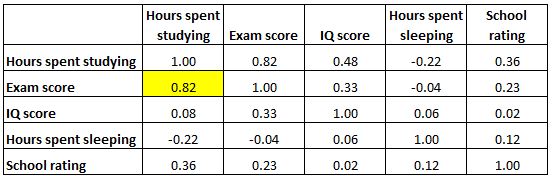
Podświetlona komórka poniżej pokazuje, że korelacja między „godzinami spędzonymi na nauce” a „godzinami spędzonymi na spaniu” wynosi -0,22 , co wskazuje, że są one słabo skorelowane ujemnie. Więcej godzin spędzonych na nauce wiąże się z mniejszą liczbą godzin spędzonych na spaniu.
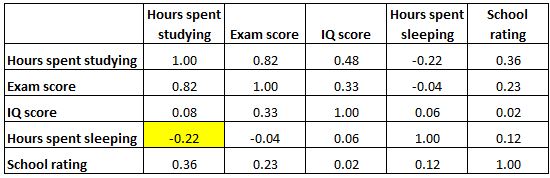
Podświetlona komórka poniżej pokazuje, że korelacja między „godzinami spędzonymi na spaniu” a „wynikiem IQ” wynosi 0,06 , co wskazuje, że są one w zasadzie nieskorelowane. Istnieje bardzo niewielki związek pomiędzy liczbą godzin snu ucznia a jego IQ.
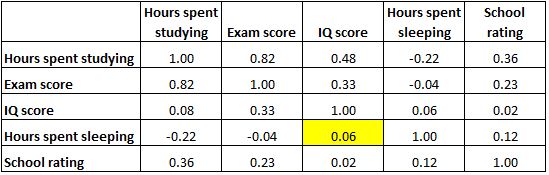
Należy również zauważyć, że wszystkie współczynniki korelacji wzdłuż przekątnej tabeli są równe 1, ponieważ każda zmienna jest doskonale skorelowana ze sobą. Komórki te nie są przydatne do interpretacji.
Odmiany macierzy korelacji
Należy pamiętać, że macierz korelacji jest idealnie symetryczna. Na przykład komórka w prawym górnym rogu pokazuje dokładnie tę samą wartość, co komórka w lewym dolnym rogu:
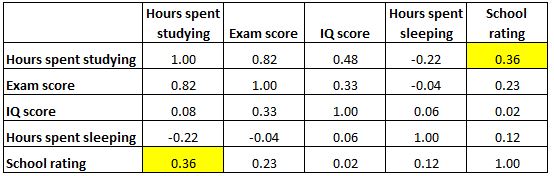
Rzeczywiście, te dwie komórki mierzą korelację między „godzinami spędzonymi na nauce” a „ocenami w szkole”.
Ponieważ macierz korelacji jest symetryczna, połowa współczynników korelacji wyświetlanych w macierzy jest zbędna i zbędna. Czasami więc wyświetlana będzie tylko połowa macierzy korelacji:
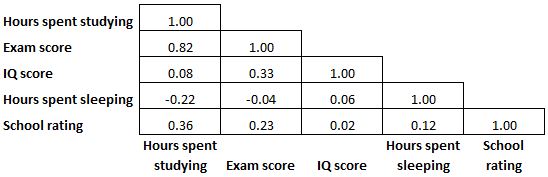
Czasami macierz korelacji będzie pokolorowana jak mapa cieplna, aby współczynniki korelacji były jeszcze łatwiejsze do odczytania:

Kiedy stosować macierz korelacji
W praktyce macierz korelacji jest powszechnie stosowana z trzech powodów:
1. Macierz korelacji w wygodny sposób podsumowuje zbiór danych.
Macierz korelacji to prosty sposób podsumowania korelacji pomiędzy wszystkimi zmiennymi w zbiorze danych. Załóżmy na przykład, że mamy następujący zbiór danych zawierający następujące informacje dotyczące 1000 uczniów:
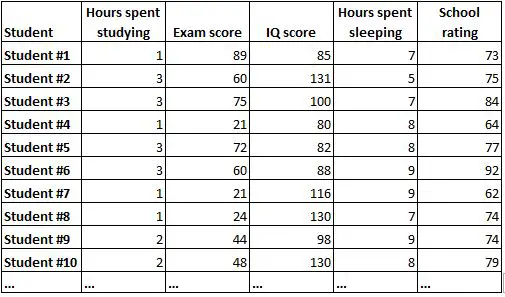
Bardzo trudno byłoby zrozumieć związek pomiędzy każdą zmienną na podstawie samych surowych danych. Na szczęście macierz korelacji może pomóc nam szybko zrozumieć korelacje pomiędzy każdą parą zmiennych.
2. Macierz korelacji służy jako diagnoza regresji.
Jednym z kluczowych założeń wielokrotnej regresji liniowej jest to, że żadna zmienna niezależna w modelu nie jest silnie skorelowana z jakąkolwiek inną zmienną w modelu.
Gdy dwie zmienne niezależne są silnie skorelowane, skutkuje to problemem zwanym współliniowością i może utrudniać interpretację wyników regresji.
Jednym z najprostszych sposobów wykrycia potencjalnego problemu współliniowości jest spojrzenie na macierz korelacji i wizualne sprawdzenie, czy którakolwiek ze zmiennych jest ze sobą silnie skorelowana.
3. Macierz korelacji można wykorzystać jako dane wejściowe do innych analiz.
Macierz korelacji służy jako dane wejściowe do innych złożonych analiz, takich jak eksploracyjna analiza czynnikowa i modele równań strukturalnych.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak utworzyć macierz korelacji przy użyciu różnych programów statystycznych:
Jak utworzyć macierz korelacji w programie Excel
Jak utworzyć macierz korelacji w SPSS
Jak utworzyć macierz korelacji w Stata
Jak utworzyć macierz korelacji w Pythonie