Jak czytać macierz kowariancji

Kowariancja jest miarą tego, jak zmiany jednej zmiennej są powiązane ze zmianami drugiej zmiennej. Mówiąc dokładniej, jest to miara stopnia, w jakim dwie zmienne są liniowo powiązane.

Macierz kowariancji to macierz kwadratowa, która pokazuje kowariancję pomiędzy wieloma różnymi zmiennymi. Może to być przydatny sposób zrozumienia, w jaki sposób różne zmienne są powiązane w zbiorze danych.

Poniższy przykład pokazuje, jak w praktyce czytać macierz kowariancji.

Jak czytać macierz kowariancji

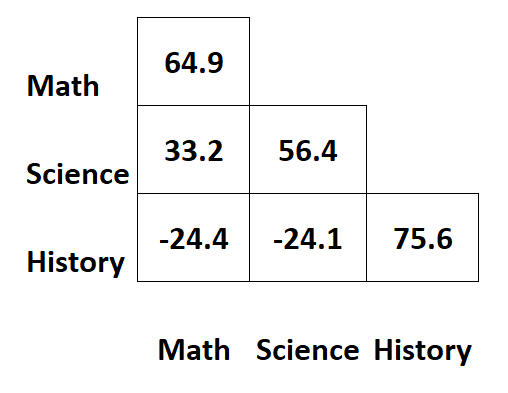
Załóżmy, że mamy następującą macierz kowariancji, która zawiera informacje o wynikach uczniów z egzaminów z trzech różnych przedmiotów:

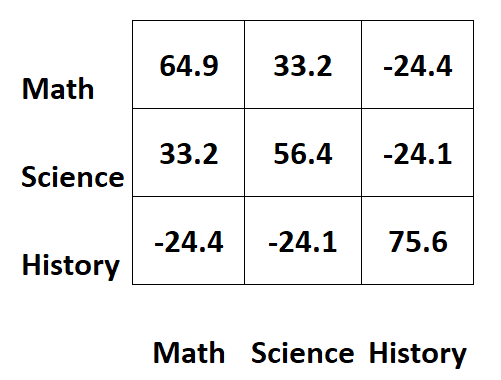
Wartości wzdłuż przekątnych macierzy reprezentują wariancje każdego przedmiotu.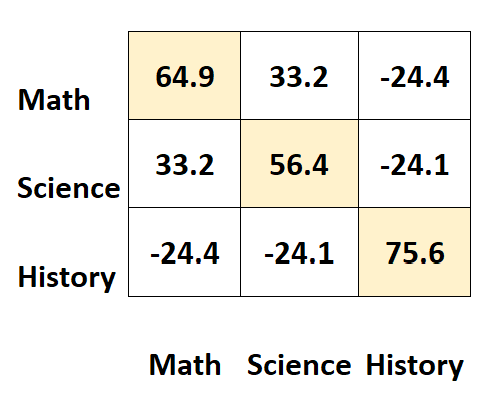

Na przykład:

• Wariancja wyników matematycznych wynosi 64,9 .
• Wariancja wyników z przedmiotów ścisłych wynosi 56,4 .
• Wariancja wyników historycznych wynosi 75,6 .

Pozostałe wartości macierzy reprezentują kowariancje pomiędzy różnymi podmiotami.

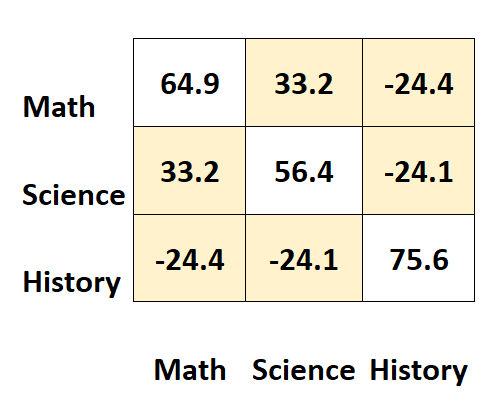
Na przykład:

• Kowariancja między wynikami z matematyki i przedmiotów ścisłych wynosi 33,2 .
• Kowariancja między wynikami z matematyki i historii wynosi –24,4 .
• Kowariancja między wynikami z nauk ścisłych i historii wynosi –24,1 .

Dodatnia liczba kowariancji wskazuje, że dwie zmienne mają tendencję do wzrostu lub spadku w tandemie.

Na przykład matematyka i przedmioty ścisłe mają dodatnią kowariancję ( 33,2 ), co wskazuje, że uczniowie, którzy osiągają dobre wyniki w matematyce, zwykle osiągają wysokie wyniki w przedmiotach ścisłych.

I odwrotnie, uczniowie, którzy osiągają słabe wyniki w matematyce, zwykle osiągają słabe wyniki w naukach ścisłych.

Ujemna liczba kowariancji wskazuje, że w miarę wzrostu jednej zmiennej druga zmienna ma tendencję do zmniejszania się.

Na przykład matematyka i historia mają ujemną kowariancję ( -24,44 ), co wskazuje, że uczniowie osiągający dobre wyniki z matematyki zwykle osiągają słabe wyniki z historii.

I odwrotnie, uczniowie, którzy osiągają niskie wyniki z matematyki, zwykle osiągają wysokie wyniki z historii.

Uwaga o symetrii macierzy kowariancji

Należy zauważyć, że macierz kowariancji jest idealnie symetryczna.

Na przykład komórka w prawym górnym rogu pokazuje dokładnie tę samą wartość, co komórka w lewym dolnym rogu:

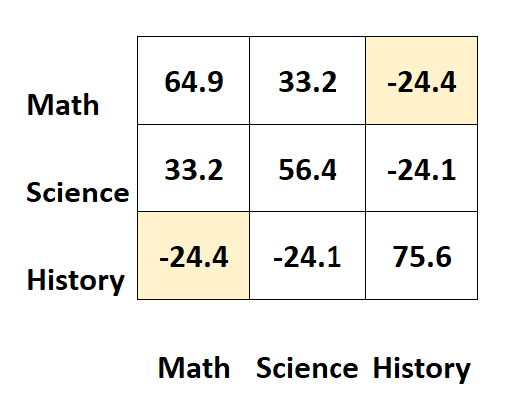
Rzeczywiście, te dwie komórki mierzą kowariancję między historią a matematyką.

Ponieważ macierz kowariancji jest symetryczna, połowa wartości kowariancji wyświetlanych w macierzy jest zbędna i niepotrzebna.

Czasami więc wyświetlana będzie tylko połowa macierzy kowariancji:

Kiedy stosować macierz kowariancji

W praktyce często będziesz musiał tworzyć i interpretować macierz korelacji częściej niż macierz kowariancji.

Jednak macierze kowariancji są często używane „pod maską” w różnych algorytmach i modelach uczenia maszynowego.

Na przykład macierz kowariancji jest używana podczas analizy głównych składowych , co pomaga nam zrozumieć podstawowe wzorce w zbiorze danych zawierającym dużą liczbę zmiennych.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak utworzyć macierz kowariancji przy użyciu różnych programów statystycznych:

Jak utworzyć macierz kowariancji w R
Jak utworzyć macierz kowariancji w Pythonie
Jak utworzyć macierz kowariancji w SPSS
Jak utworzyć macierz kowariancji w programie Excel