Jak czytać wykres pudełkowy z wartościami odstającymi (z przykładem)

Wykres pudełkowy to rodzaj wykresu przedstawiający pięciocyfrowe podsumowanie zbioru danych, które obejmuje:

• Wartość minimalna
• Pierwszy kwartyl (25. percentyl)
• Wartość średnia
• Trzeci kwartyl (75. percentyl)
• Maksymalna wartość

Aby sporządzić wykres pudełkowy, najpierw rysujemy pudełko od pierwszego do trzeciego kwartyla.

Następnie rysujemy pionową linię na środku.

Na koniec rysujemy „wąsy” kwartylów aż do wartości minimalnej i maksymalnej.

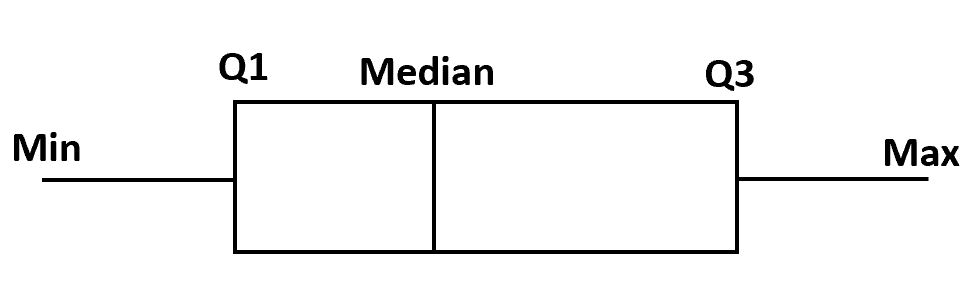
W większości programów statystycznych obserwację definiuje się jako wartość odstającą, jeśli spełnia jeden z dwóch poniższych wymagań:

• Obserwacja jest 1,5-krotnością rozstępu międzykwartylowego poniżej pierwszego kwartyla (Q1)
• Obserwacja jest 1,5-krotnością rozstępu międzykwartylowego powyżej trzeciego kwartyla (Q3).

Jeśli w zbiorze danych występuje wartość odstająca, jest ona zwykle oznaczona małą kropką poza zakresem wąsów na wykresie pudełkowym:

Kiedy tak się dzieje, wartościom „minimalnym” i „maksymalnym” na wykresie pudełkowym po prostu przypisuje się wartości Q1 – odpowiednio 1,5*IQR i Q3 + 1,5*IQR.

Poniższy przykład pokazuje, jak interpretować wykresy pudełkowe z wartościami odstającymi i bez nich.

Przykład: interpretacja wykresu pudełkowego z wartościami odstającymi

Załóżmy, że tworzymy następujące dwa wykresy pudełkowe, aby zwizualizować rozkład punktów zdobytych przez koszykarzy z dwóch różnych drużyn:

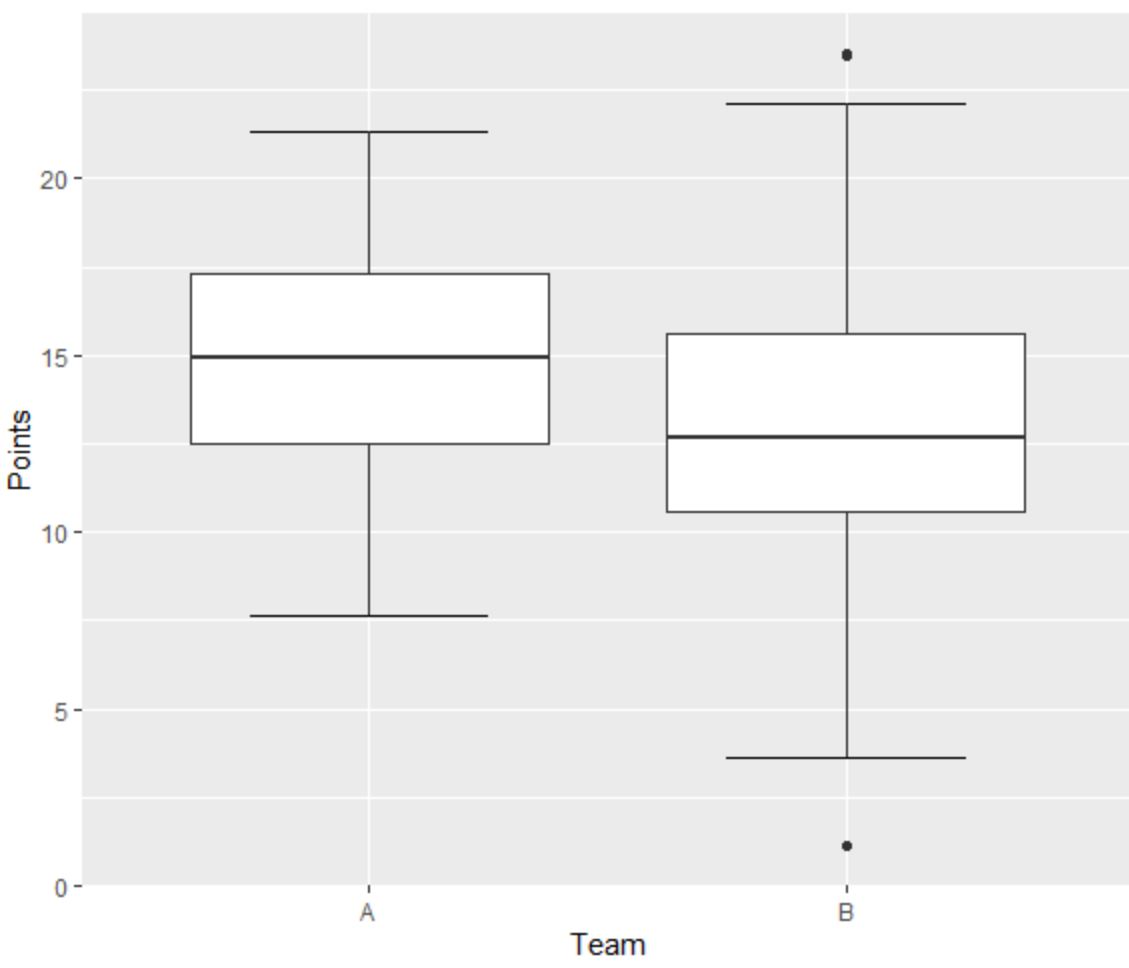
Lewy wykres pudełkowy dla Drużyny A nie zawiera wartości odstających, ponieważ nie ma małych kropek znajdujących się poza minimalnym lub maksymalnym wąsem.

Jednakże właściwy wykres pudełkowy dla Zespołu B zawiera jedną wartość odstającą powyżej wartości „maksymalnej” i jedną wartość odstającą poniżej wartości „minimalnej”.

Oto aktualne pięciocyfrowe podsumowanie podziału zmiennej „Punkty” dla Drużyny B:

• Wartość minimalna: 1,1
• Pierwszy kwartyl: 10,5
• Mediana: 12,7
• Trzeci kwartyl: 15,6
• Wartość maksymalna: 23,5

Oto jak obliczyć granice potencjalnych wartości odstających:

Skala międzykwartylowa : Trzeci kwartyl – Pierwszy kwartyl = 15,6 – 10,5 = 5,1

Dolna granica : Q1 – 1,5*IQR = 10,5 – 1,5*5,1 = 2,85

Górna granica : Q3 + 1,5*IQR = 15,6 + 1,5*5,1 = 23,25

Wąsy dla wartości minimalnej i maksymalnej na wykresie pudełkowym znajdują się przy 2,85 i 23,25 .

Zatem obserwacje o wartościach 1,1 i 23,5 kwalifikują się jako wartości odstające na wykresie pudełkowym, ponieważ wykraczają poza dolną i górną granicę.

Bonus : Oto dokładny kod, którego użyliśmy do stworzenia tych dwóch wykresów skrzynkowych w języku programowania R:

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat wykresów pudełkowych:

Jak porównać wykresy pudełkowe
Jak rozpoznać asymetrię na wykresach pudełkowych
Jak znaleźć rozstęp międzykwartylowy wykresu pudełkowego