Jak interpretować resztkowy błąd standardowy

Resztkowy błąd standardowy służy do pomiaru dopasowania modelu regresji do zbioru danych.

W uproszczeniu mierzy odchylenie standardowe reszt w modelu regresji.

Oblicza się go w następujący sposób:

Resztkowy błąd standardowy = √ Σ(y – ŷ) ² /df

Złoto:

• y: Obserwowana wartość
• ŷ: Przewidywana wartość
• df: Stopnie swobody obliczone jako całkowita liczba obserwacji – całkowita liczba parametrów modelu.

Im mniejszy resztkowy błąd standardowy, tym lepiej model regresji pasuje do zbioru danych. I odwrotnie, im wyższy resztkowy błąd standardowy, tym gorzej model regresji pasuje do zbioru danych.

Model regresji, który ma mały resztkowy błąd standardowy, będzie miał punkty danych ściśle skupione wokół dopasowanej linii regresji:

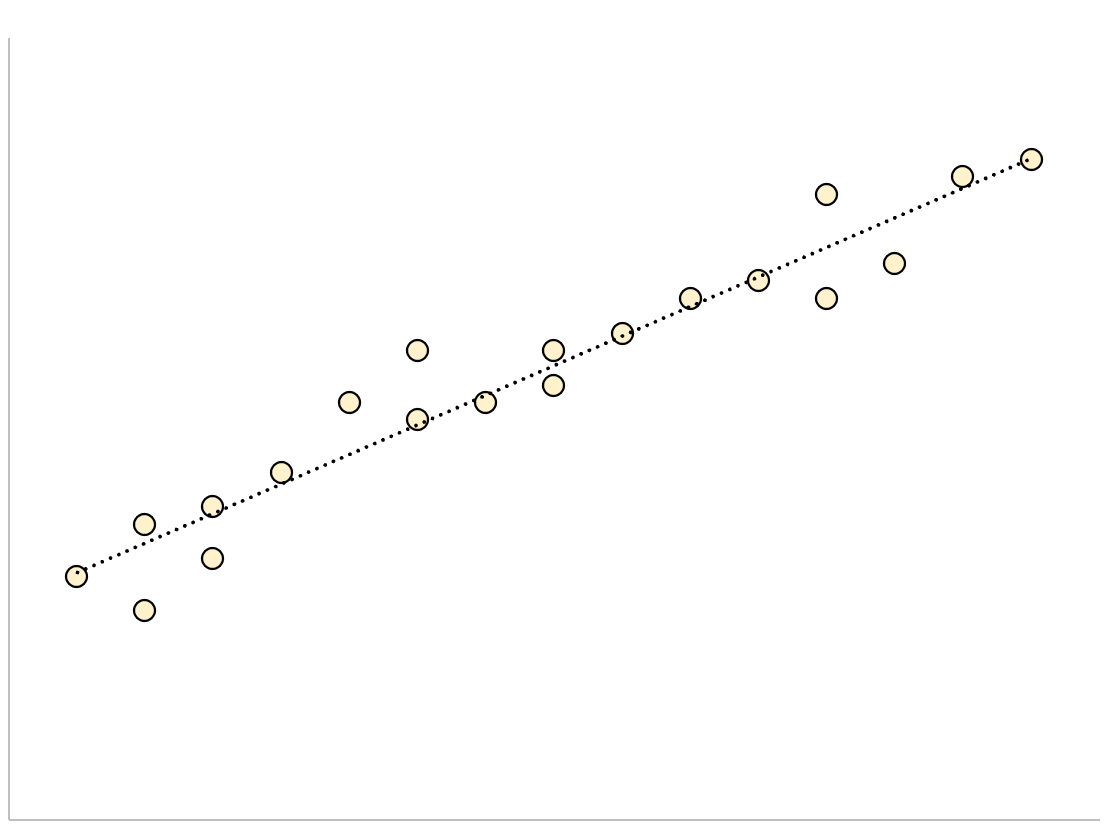
Reszty tego modelu (różnica między wartościami obserwowanymi a wartościami przewidywanymi) będą małe, co oznacza, że resztkowy błąd standardowy również będzie niewielki.

I odwrotnie, model regresji, który ma duży resztkowy błąd standardowy, będzie miał punkty danych bardziej luźno rozproszone wokół dopasowanej linii regresji:

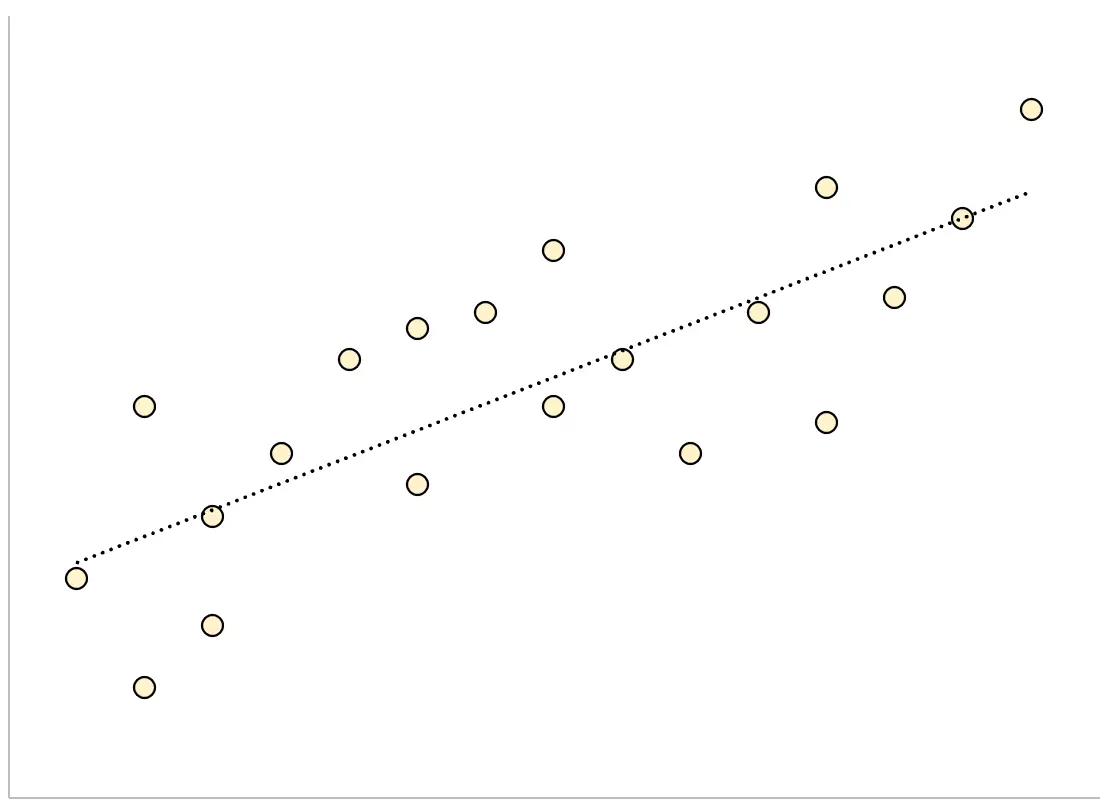
Reszty z tego modelu będą większe, co oznacza, że resztowy błąd standardowy również będzie większy.

Poniższy przykład pokazuje, jak obliczyć i zinterpretować resztkowy błąd standardowy modelu regresji w R.

Przykład: Interpretacja resztkowego błędu standardowego

Załóżmy, że chcemy dopasować następujący model regresji liniowej:

mpg = β ₀ + β ₁ (wyporność) + β ₂ (moc)

Model ten wykorzystuje zmienne predykcyjne „pojemność” i „moc”, aby przewidzieć liczbę mil na galon przejechany przez dany samochód.

Poniższy kod pokazuje, jak dopasować ten model regresji w R:

 #load built-in mtcars dataset
data(mtcars)

#fit regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Call:
lm(formula = mpg ~ disp + hp, data = mtcars)

Residuals:
    Min 1Q Median 3Q Max 
-4.7945 -2.3036 -0.8246 1.8582 6.9363 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

W dolnej części wyniku widzimy, że resztkowy błąd standardowy tego modelu wynosi 3,127 .

To mówi nam, że model regresji przewiduje mpg samochodu ze średnim błędem około 3127.

Stosowanie resztkowego błędu standardowego do porównywania modeli

Resztkowy błąd standardowy jest szczególnie przydatny do porównywania dopasowania różnych modeli regresji.

Załóżmy na przykład, że dopasowujemy dwa różne modele regresji, aby przewidzieć zużycie paliwa w samochodzie. Resztkowy błąd standardowy każdego modelu jest następujący:

• Błąd standardowy szczątkowy modelu 1: 3,127
• Resztkowy błąd standardowy modelu 2: 5,657

Ponieważ Model 1 ma niższy błąd standardowy rezydualny, lepiej pasuje do danych niż Model 2. Dlatego wolelibyśmy używać Modelu 1 do przewidywania mpg samochodu, ponieważ przewidywania, które tworzy, są bliższe obserwowanym wartościom mpg samochodów.

Dodatkowe zasoby

Jak wykonać prostą regresję liniową w R
Jak wykonać wielokrotną regresję liniową w R
Jak utworzyć wykres rezydualny w R