Jak interpretować błąd średniokwadratowy (rmse)

Analiza regresji to technika, której możemy użyć do zrozumienia związku pomiędzy jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Jednym ze sposobów oceny, jak dobrze model regresji pasuje do zbioru danych, jest obliczenie błędu średniokwadratowego , który jest metryką, która mówi nam średnią odległość między wartościami przewidywanymi modelu a rzeczywistymi wartościami zbioru danych.

Im niższy RMSE, tym lepiej dany model jest w stanie „dopasować” zbiór danych.

Wzór na znalezienie błędu średniokwadratowego, często w skrócie RMSE , jest następujący:

RMSE = √ Σ(P _ja – O _ja ) ² / n

Złoto:

• Σ to fantazyjny symbol oznaczający „sumę”
• _Pi jest przewidywaną wartością ^i-tej obserwacji w zbiorze danych
• O _i jest obserwowaną wartością ^i-tej obserwacji w zbiorze danych
• n to wielkość próbki

Poniższy przykład pokazuje, jak interpretować RMSE dla danego modelu regresji.

Przykład: Jak interpretować RMSE dla modelu regresji

Załóżmy, że chcemy zbudować model regresji, który wykorzystuje „przepracowane godziny” do przewidywania „ocen” uczniów z konkretnego egzaminu wstępnego na studia.

Gromadzimy następujące dane dla 15 uczniów:

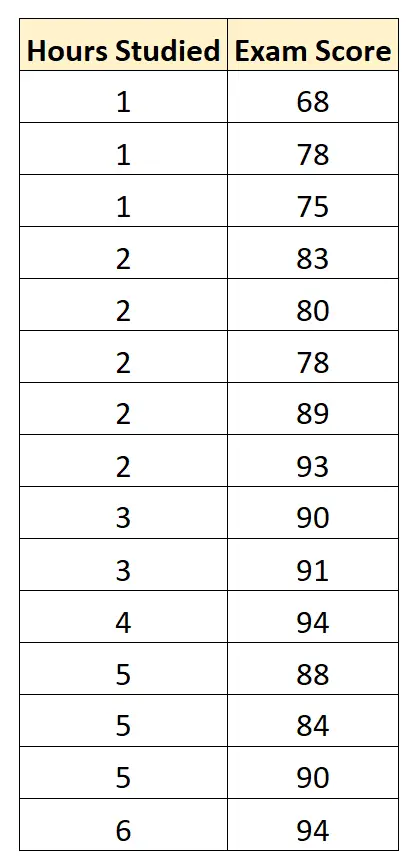
Następnie korzystamy z oprogramowania statystycznego (takiego jak Excel, SPSS, R, Python) itp. znaleźć następujący dopasowany model regresji:

Wynik egzaminu = 75,95 + 3,08* (godziny nauki)

Możemy następnie użyć tego równania, aby przewidzieć wynik egzaminu każdego ucznia na podstawie liczby godzin, których się uczył:

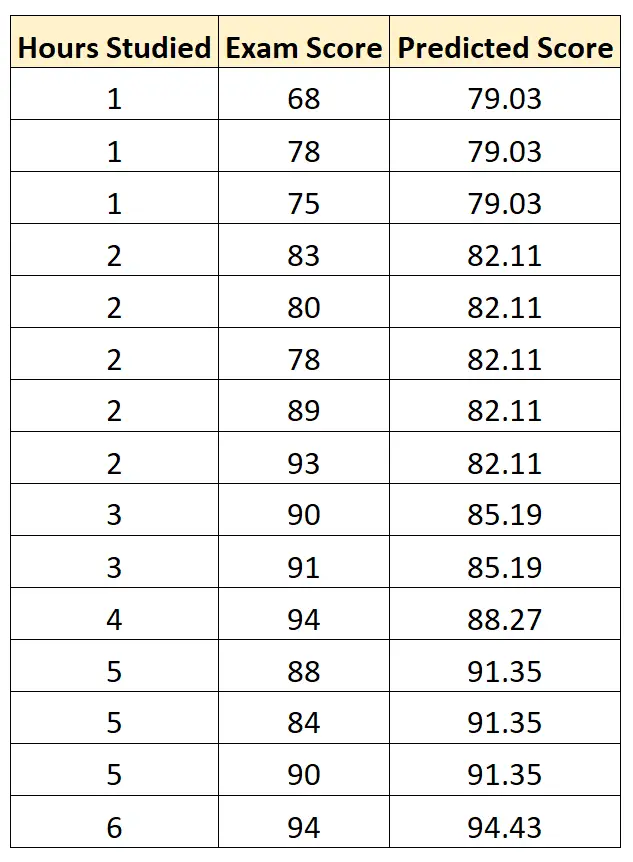
Następnie możemy obliczyć kwadratową różnicę między przewidywanym wynikiem każdego egzaminu a rzeczywistym wynikiem egzaminu. Następnie możemy obliczyć pierwiastek kwadratowy średniej tych różnic:

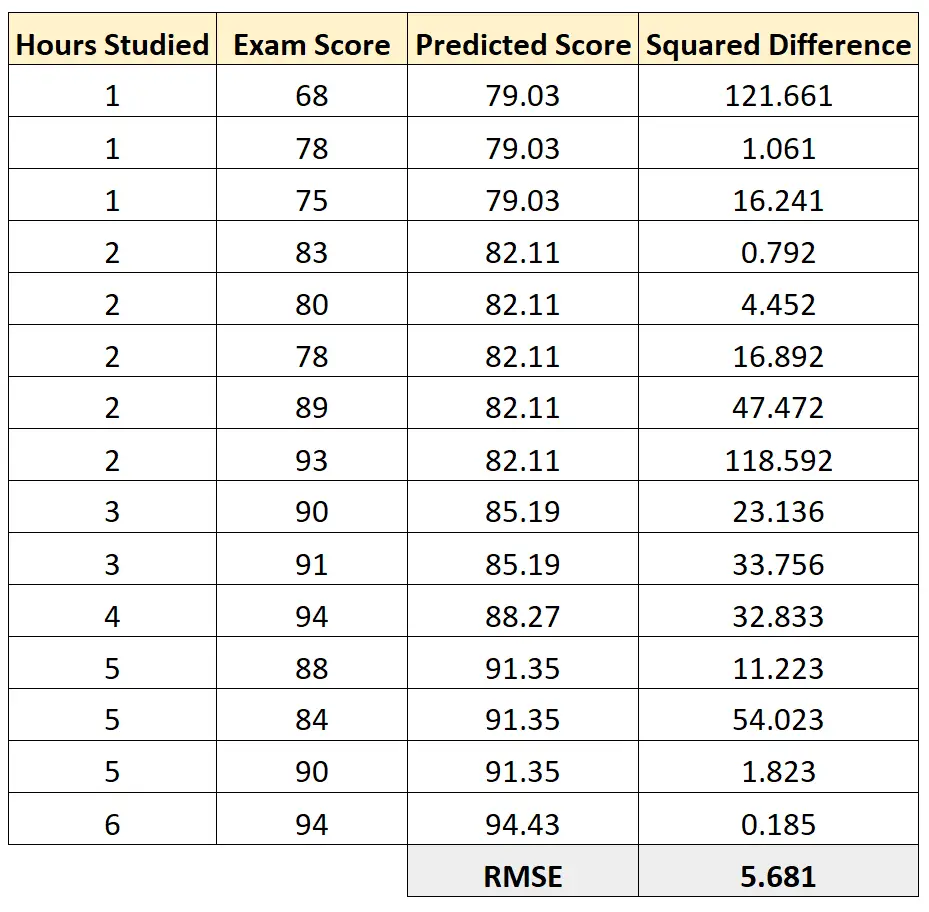
RMSE tego modelu regresji wynosi 5,681 .

Przypomnijmy, że reszty modelu regresji to różnice między obserwowanymi wartościami danych a przewidywanymi wartościami modelu.

Reszta = (P _i – O _i )

Złoto

• _Pi jest przewidywaną wartością ^i-tej obserwacji w zbiorze danych
• O _i jest obserwowaną wartością ^i-tej obserwacji w zbiorze danych

Pamiętaj, że RMSE modelu regresji oblicza się w następujący sposób:

RMSE = √ Σ(P _ja – O _ja ) ² / n

Oznacza to, że RMSE reprezentuje pierwiastek kwadratowy wariancji reszt.

Jest to przydatna wartość, ponieważ daje nam wyobrażenie o średniej odległości między obserwowanymi wartościami danych a przewidywanymi wartościami danych.

Kontrastuje to z R-kwadratem modelu, który mówi nam, jaką część wariancji zmiennej odpowiedzi można wyjaśnić zmienną(ami) predykcyjną modelu.

Porównanie wartości RMSE różnych modeli

RMSE jest szczególnie przydatny do porównywania dopasowania różnych modeli regresji.

Załóżmy na przykład, że chcemy zbudować model regresji do przewidywania wyników egzaminów uczniów i chcemy znaleźć najlepszy możliwy model spośród kilku potencjalnych modeli.

Załóżmy, że dopasowujemy trzy różne modele regresji i znajdujemy odpowiadające im wartości RMSE:

• RMSE modelu 1: 14,5
• RMSE modelu 2: 16,7
• RMSE modelu 3: 9,8

Model 3 ma najniższy RMSE, co mówi nam, że jest w stanie najlepiej dopasować zbiór danych spośród trzech potencjalnych modeli.

Dodatkowe zasoby

Kalkulator RMSE
Jak obliczyć RMSE w Excelu
Jak obliczyć RMSE w R
Jak obliczyć RMSE w Pythonie