Jak ręcznie obliczyć wartość p z testu t

Jednym z najczęściej stosowanych testów w statystyce jest test t , który jest często używany do ustalenia, czy średnia populacji jest równa określonej wartości.

Załóżmy na przykład, że chcemy wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali. Aby to przetestować, moglibyśmy zebrać losową próbkę 20 roślin, znaleźć średnią próbki i odchylenie standardowe próbki, a następnie wykonać test t, aby ustalić, czy średnia wysokość wynosi w rzeczywistości 15 cali.

Hipotezy zerowe i alternatywne testu są następujące:

_H0 : µ = 15

H _a : µ ≠ 15

Wzór na statystykę testową to:

t = ( X -μ) / (s/ √n )

gdzie x to średnia próbki, μ to hipotetyczna średnia (w naszym przykładzie będzie to 15), s to odchylenie standardowe próbki, a n to wielkość próbki.

Kiedy już znamy wartość t , możemy użyć oprogramowania statystycznego lub kalkulatora internetowego , aby znaleźć odpowiednią wartość p. Jeśli wartość p jest poniżej pewnego poziomu alfa (najczęściej wybierane wartości to 0,01, 0,05 i 0,10), wówczas możemy odrzucić hipotezę zerową i stwierdzić, że średnia wysokość rośliny przy 15 calach nie jest równa.

Jednakże możliwe jest również ręczne oszacowanie testowej wartości p przy użyciu tabeli rozkładu t . W tym artykule wyjaśnimy, jak to zrobić.

Przykład: ręczne obliczenie wartości p z testu t

Problem : Bob chce wiedzieć, czy średnia wysokość określonego gatunku rośliny wynosi 15 cali. Aby to sprawdzić, zbiera losową próbkę 20 roślin i stwierdza, że średnia próbki wynosi 14 cali, a odchylenie standardowe próbki wynosi 3 cale. Wykonaj test t, używając poziomu alfa 0,05, aby określić, czy rzeczywista średnia wysokość populacji wynosi w rzeczywistości 15 cali.

Rozwiązanie:

Krok 1: Podaj hipotezę zerową i alternatywną.

_H0 : µ = 15

H _a : µ ≠ 15

Krok 2: Znajdź statystykę testową.

t = ( x -μ) / (s/ √n ) = (14-15) / (3/ √20 ) = -1,49

Krok 3: Znajdź wartość p dla statystyki testowej.

Aby ręcznie znaleźć wartość p, musimy skorzystać z tabeli rozkładu t z n-1 stopniami swobody. W naszym przykładzie wielkość naszej próby wynosi n = 20, więc n-1 = 19.

W poniższej tabeli rozkładu t musimy spojrzeć na wiersz odpowiadający „19” po lewej stronie i spróbować znaleźć wartość bezwzględną naszej statystyki testowej 1,49 .

Należy pamiętać, że 1,49 nie pojawia się w tabeli, ale mieści się pomiędzy dwiema wartościami 1,328 i 1,729 .

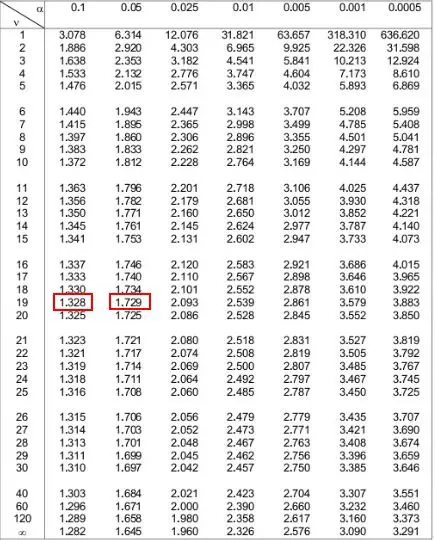
Następnie możemy przyjrzeć się dwóm poziomom alfa u góry tabeli, które odpowiadają tym dwóm liczbom. Widzimy, że wynoszą one 0,1 i 0,05 .

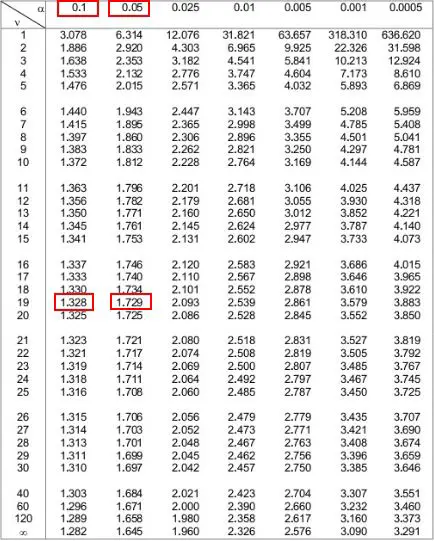
Oznacza to, że wartość p dla testu jednostronnego mieści się w przedziale od 0,1 do 0,05. Nazwijmy to 0,075. Ponieważ nasz test t jest dwustronny, musimy pomnożyć tę wartość przez 2. Zatem nasza szacunkowa wartość p wynosi 0,075 * 2 = 0,15 .

Krok 4: Wyciągnij wnioski.

Ponieważ ta wartość p nie jest niższa niż wybrany poziom alfa wynoszący 0,05, nie możemy odrzucić hipotezy zerowej. Zatem nie mamy wystarczających dowodów, aby stwierdzić, że prawdziwa średnia wysokość tego gatunku rośliny jest inna niż 15 cali.

Sprawdź wyniki za pomocą kalkulatora

Możemy podłączyć naszą statystykę testu t i stopnie swobody do internetowego kalkulatora wartości p, aby zobaczyć, jak blisko naszej szacunkowej wartości p była rzeczywista wartość p:

Prawdziwa wartość p wynosi 0,15264 , co jest całkiem blisko naszej szacunkowej wartości p wynoszącej 0,15 .

Wniosek

W tym artykule widzieliśmy, że możliwe jest ręczne oszacowanie wartości p testu t przy użyciu tabeli rozkładu t. Jednak w większości scenariuszy nigdy nie będzie konieczne ręczne obliczanie wartości p i można użyć oprogramowania statystycznego, takiego jak R i Excel, lub kalkulatora internetowego, aby znaleźć dokładną wartość p testu.

W większości przypadków, zwłaszcza w przypadku rygorystycznych badań statystycznych i eksperymentów, będziesz chciał użyć kalkulatora, aby znaleźć dokładną wartość p z testu t tak precyzyjnie, jak to tylko możliwe, ale dobrze jest wiedzieć, że zawsze możesz ręcznie oszacować wartość p z testu t, jeśli jest to absolutnie konieczne.