Jak obliczyć vif w excelu

Wielokolinearność w analizie regresji ma miejsce, gdy dwie lub więcej zmiennych objaśniających jest ze sobą silnie skorelowanych, w związku z czym nie dostarczają unikalnych lub niezależnych informacji w modelu regresji. Jeśli stopień korelacji między zmiennymi jest wystarczająco wysoki, może to powodować problemy podczas dopasowywania i interpretacji modelu regresji.

Na szczęście możliwe jest wykrycie wieloliniowości za pomocą metryki zwanej współczynnikiem inflacji wariancji (VIF) , która mierzy korelację i siłę korelacji pomiędzy zmiennymi objaśniającymi w modelu regresji.

W tym samouczku wyjaśniono, jak obliczyć VIF w programie Excel.

Przykład: obliczanie VIF w Excelu

W tym przykładzie przeprowadzimy wielokrotną regresję liniową, korzystając z następującego zbioru danych opisującego atrybuty 10 koszykarzy. Dopasujemy model regresji, wykorzystując rating jako zmienną reakcji oraz punkty, asysty i zbiórki jako zmienne objaśniające. Następnie zidentyfikujemy wartości VIF dla każdej zmiennej objaśniającej.

Krok 1: Wykonaj wielokrotną regresję liniową.

Na górnej wstążce przejdź do karty Dane i kliknij Analiza danych. Jeśli nie widzisz tej opcji, musisz najpierw zainstalować bezpłatne oprogramowanie Analysis ToolPak .

Po kliknięciu Analiza danych pojawi się nowe okno. Wybierz opcję Regresja i kliknij OK.

Wypełnij niezbędne tabele dla zmiennych odpowiedzi i zmiennych objaśniających, a następnie kliknij OK.

Daje to następujący wynik:

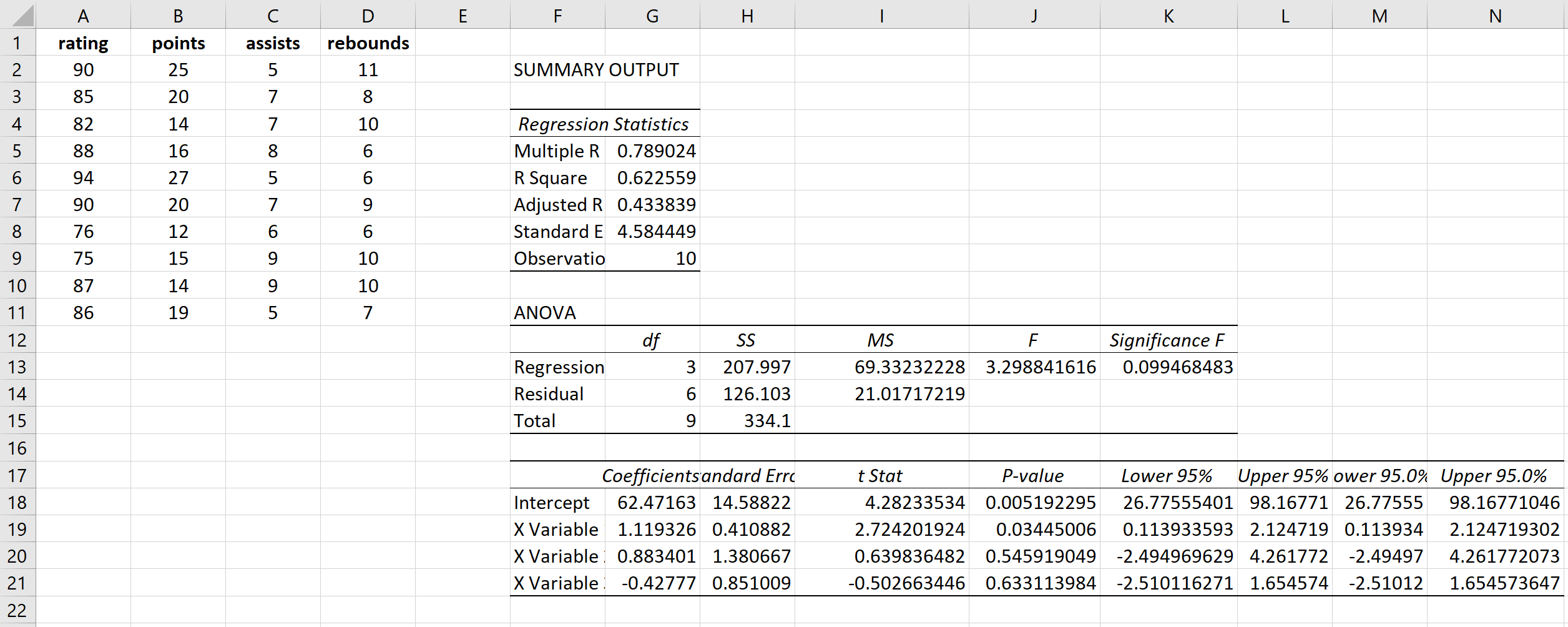
Krok 2: Oblicz VIF dla każdej zmiennej objaśniającej.

Następnie możemy obliczyć VIF dla każdej z trzech zmiennych objaśniających, wykonując indywidualne regresje, używając jednej zmiennej objaśniającej jako zmiennej odpowiedzi, a pozostałych dwóch jako zmiennych objaśniających.

Na przykład możemy obliczyć VIF dla zmiennej punktowej , wykonując wielokrotną regresję liniową, używając punktów jako zmiennej odpowiedzi oraz asyst i zbiórek jako zmiennych objaśniających.

Daje to następujący wynik:

VIF dla punktów oblicza się jako 1 / (1 – R kwadrat) = 1 / (1 – 0,433099) = 1,76 .

Następnie możemy powtórzyć ten proces dla pozostałych dwóch zmiennych, asyst i zbiórek .

Okazuje się, że współczynniki VIF dla trzech zmiennych objaśniających są następujące:

punkty: 1,76
asysty: 1,96
zbiórki: 1,18

Jak interpretować wartości VIF

Wartość VIF zaczyna się od 1 i nie ma górnej granicy. Ogólna zasada interpretacji VIF jest następująca:

• Wartość 1 oznacza, że pomiędzy daną zmienną objaśniającą a jakąkolwiek inną zmienną objaśniającą w modelu nie ma korelacji.
• Wartość od 1 do 5 wskazuje na umiarkowaną korelację pomiędzy daną zmienną objaśniającą a innymi zmiennymi objaśniającymi w modelu, jednak często nie jest ona na tyle poważna, aby wymagała szczególnej uwagi.
• Wartość większa od 5 wskazuje na potencjalnie silną korelację pomiędzy daną zmienną objaśniającą a innymi zmiennymi objaśniającymi w modelu. W tym przypadku szacunki współczynników i wartości p w wynikach regresji są prawdopodobnie niewiarygodne.

Ponieważ każda z wartości VIF zmiennych objaśniających w naszym modelu regresji jest zamknięta do 1, w naszym przykładzie wieloliniowość nie stanowi problemu.