Jak wykonać test friedmana w programie excel

Test Friedmana jest nieparametryczną alternatywą dla ANOVA z powtarzanymi pomiarami . Służy do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej grup, w których w każdej grupie występują ci sami pacjenci.

W tym samouczku wyjaśniono, jak wykonać test Friedmana w programie Excel.

Przykład: test Friedmana w Excelu

Wykonaj poniższe kroki, aby wykonać test Friedmana w programie Excel.

Krok 1: Wprowadź dane.

Wprowadź następujące dane, które pokazują czas reakcji (w sekundach) 10 pacjentów przyjmujących trzy różne leki. Ponieważ u każdego pacjenta badany jest każdy z trzech leków, użyjemy testu Friedmana, aby określić, czy średni czas reakcji różni się w zależności od leku.

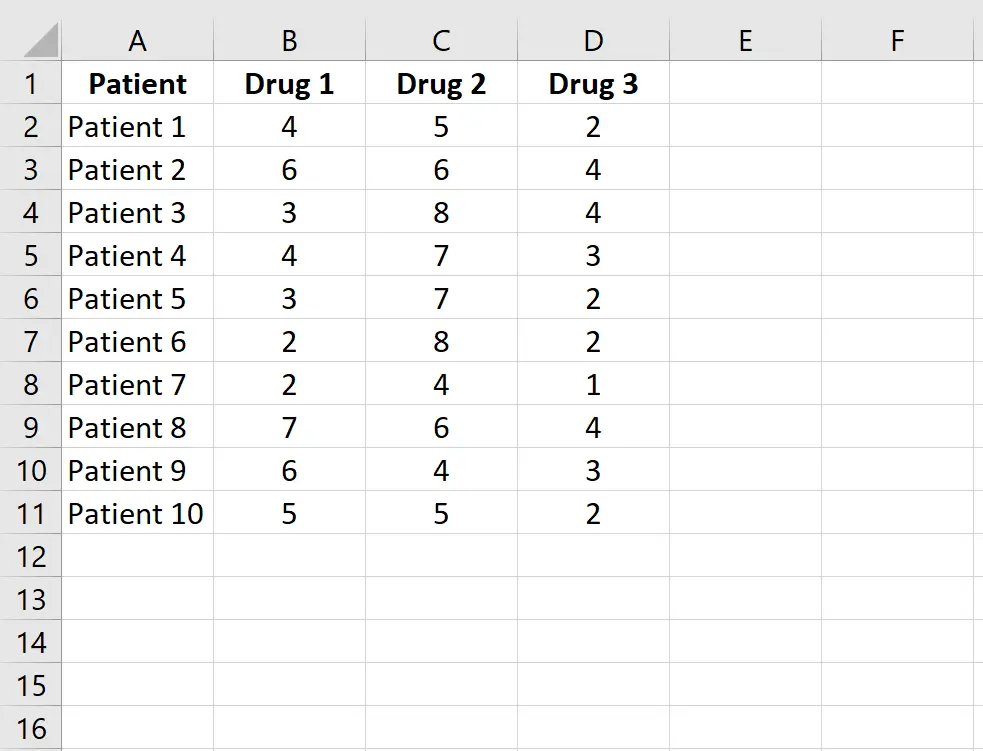
Krok 2: Sklasyfikuj dane.

Następnie uszereguj wartości danych w każdym wierszu w kolejności rosnącej, korzystając z funkcji =RANK.AVG() . Poniższy wzór pokazuje, jak obliczyć rangę czasu reakcji pacjenta 1 na lek 1:

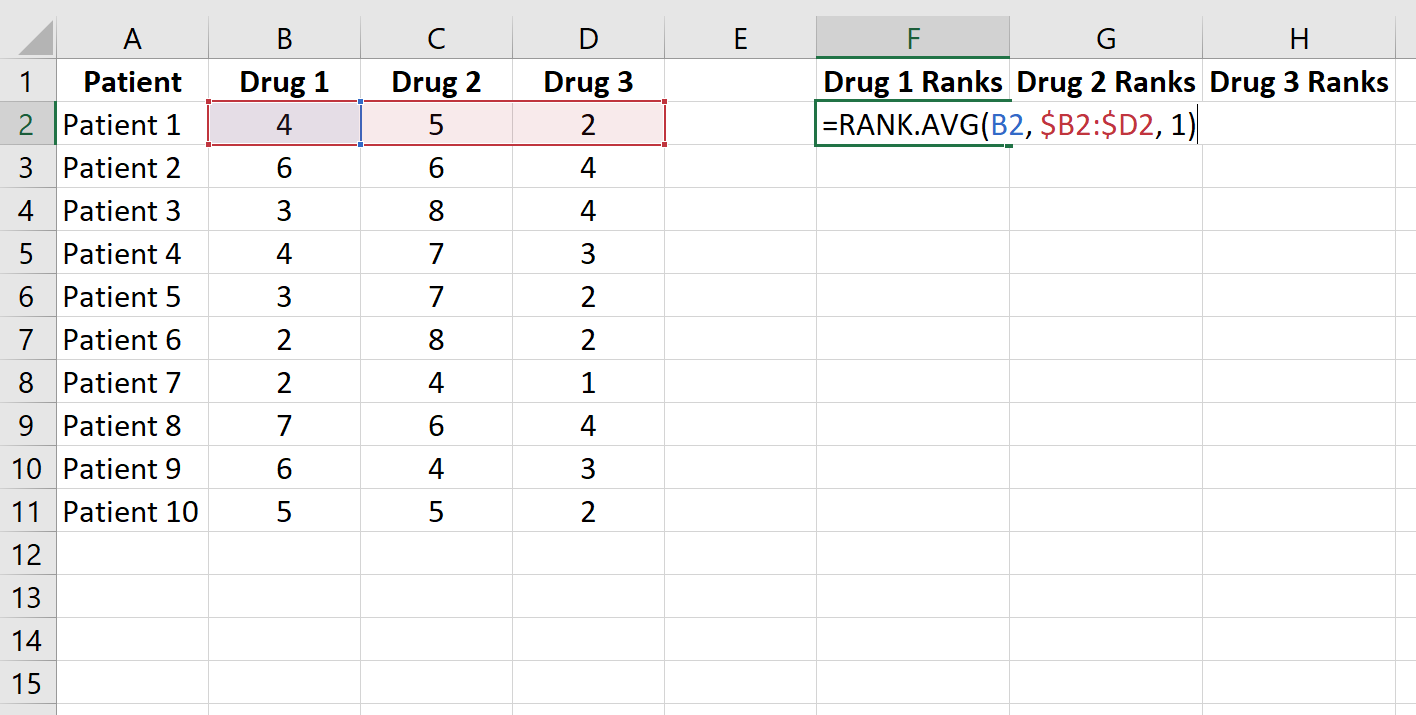
Skopiuj tę formułę do pozostałych komórek:

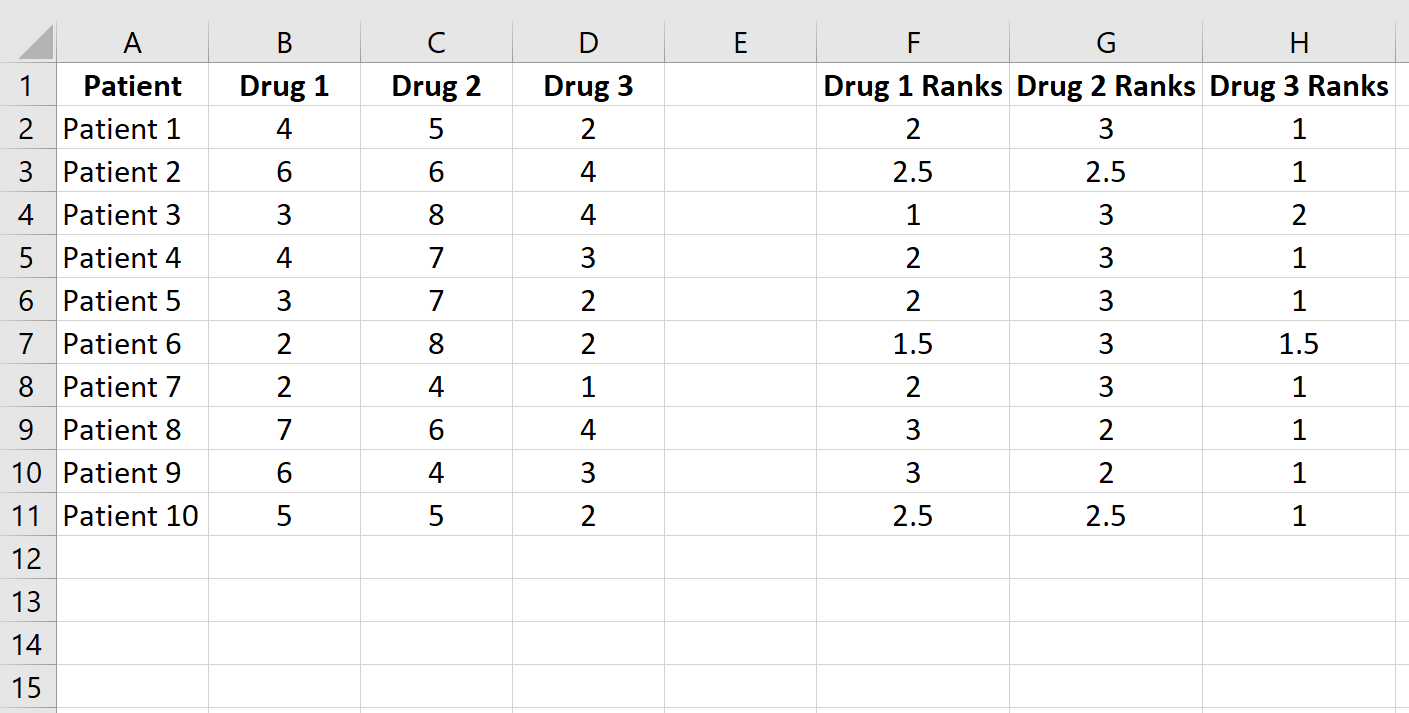
Następnie oblicz sumę rang dla każdej kolumny oraz kwadratową sumę rang:

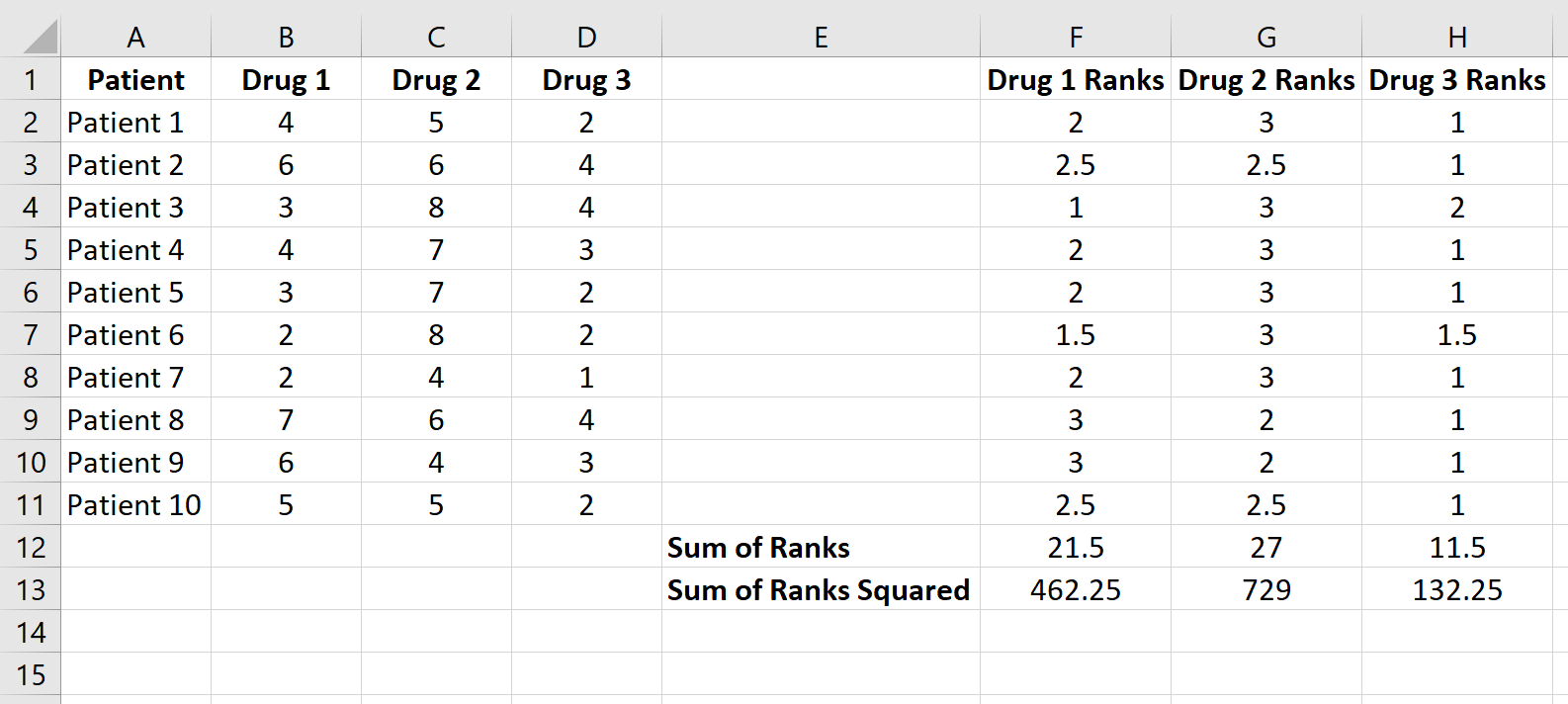
Krok 3: Oblicz statystykę testową i odpowiadającą jej wartość p.

Statystykę testową definiuje się jako:

Q = 12/nk(k+1) * ΣR _j ² – 3n(k+1)

Złoto:

• n = liczba pacjentów
• k = liczba grup terapeutycznych
• R _j ² = suma rang dla ^j-tej grupy

Zgodnie z hipotezą zerową Q ma rozkład chi-kwadrat z k-1 stopniami swobody.

Poniższy zrzut ekranu przedstawia wzory użyte do obliczenia statystyki testowej Q i odpowiadającej jej wartości p:

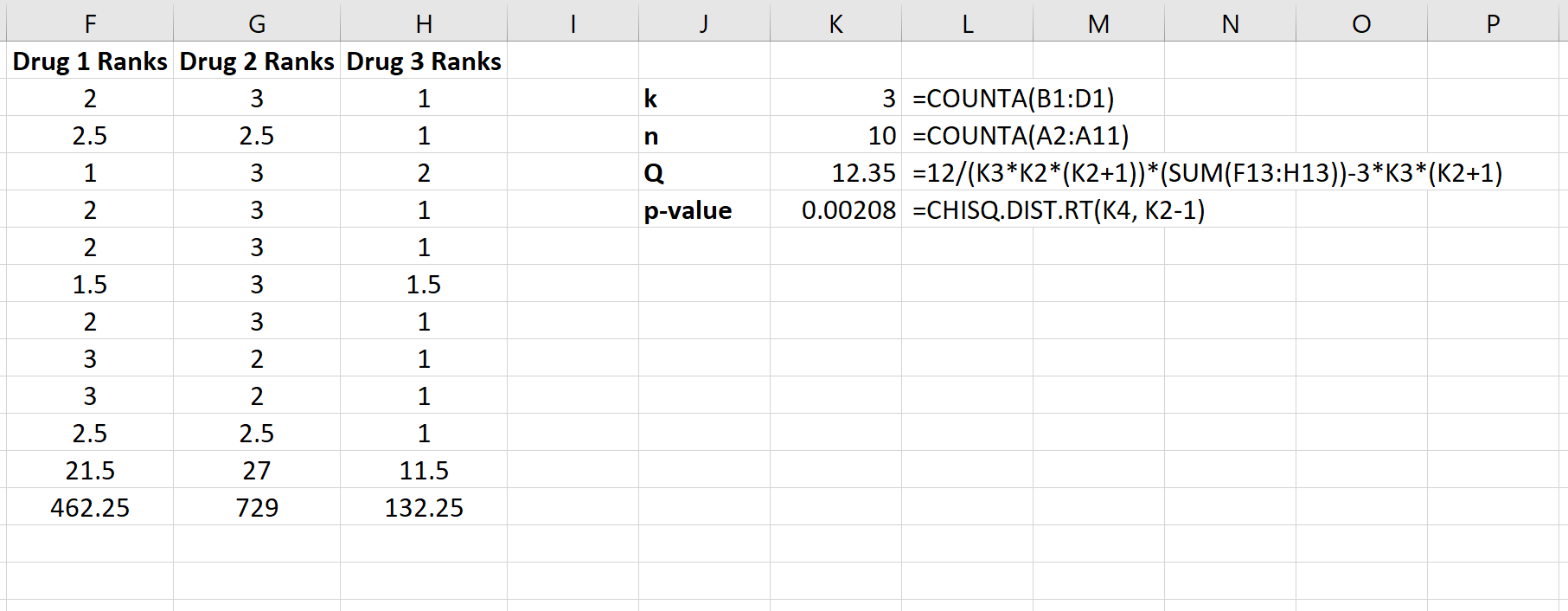
Statystyka testowa wynosi Q = 12,35 , a odpowiadająca jej wartość p wynosi p = 0,00208 . Ponieważ wartość ta jest mniejsza niż 0,05, możemy odrzucić hipotezę zerową, że średni czas reakcji jest taki sam dla wszystkich trzech leków. Mamy wystarczające dowody, aby stwierdzić, że rodzaj stosowanego leku powoduje statystycznie istotne różnice w czasie reakcji.

Krok 4: Ogłoś wyniki.

Na koniec chcielibyśmy poinformować o wynikach testów. Oto przykład, jak to zrobić:

Test Friedmana przeprowadzono na 10 pacjentach, aby sprawdzić wpływ trzech różnych leków na czas reakcji. Każdy pacjent stosował każdy lek jeden raz.

Wyniki wykazały, że rodzaj stosowanego leku wpływał na istotne statystycznie różnice w czasie odpowiedzi (Q = 12,35, p = 0,00208).