Jak znaleźć wartość p na podstawie wyniku z w programie excel

Wiele testów hipotez w statystykach skutkuje statystyką testu z. Kiedy znajdziemy tę statystykę testu z, zwykle znajdujemy powiązaną z nią wartość p. Jeśli ta wartość p jest poniżej pewnego poziomu alfa (np. 0,10, 0,05, 0,01), wówczas odrzucamy hipotezę zerową testu i stwierdzamy, że nasze wyniki są istotne.

W tym samouczku przedstawiono kilka przykładów znajdowania wartości p na podstawie wyniku Z w programie Excel przy użyciu funkcji ROZKŁ.NORMALNY , która przyjmuje następujące argumenty:

ROZKŁ.NORMALNY (x, średnia, odch.standardowa, skumulowany)

Złoto:

• x to wynik z, który nas interesuje.
• średnia jest średnią rozkładu — użyjemy „0” dla standardowego rozkładu normalnego.
• standard_dev to odchylenie standardowe rozkładu – będziemy używać „1” dla standardowego rozkładu normalnego.
• kumulatywny przyjmuje wartość „PRAWDA” (zwraca CDF) lub „FAŁSZ” (zwraca plik PDF) – z „PRAWDA” skorzystamy, aby uzyskać wartość funkcji rozkładu skumulowanego.

Zobaczmy kilka przykładów.

Przykład 1: Znajdowanie wartości P na podstawie wyniku Z (test dwustronny)

Firma chce wiedzieć, czy nowy typ baterii ma inną średnią żywotność niż obecna standardowa bateria, która ma średnią żywotność 18 godzin. W losowej próbie 100 nowych baterii stwierdzono, że średnia żywotność wynosi 19 godzin przy odchyleniu standardowym wynoszącym 4 godziny.

Wykonaj dwustronny test hipotezy, stosując poziom alfa 0,05, aby określić, czy średnia żywotność nowej baterii różni się od średniej żywotności aktualnej baterii standardowej.

Krok 1: Postaw hipotezy.

Hipoteza zerowa (H ₀ ): μ = 18

Hipoteza alternatywna: (Ha): μ ≠ 18

Krok 2: Znajdź statystykę testu z.

Statystyka testowa z = (x-μ) / (s/√n) = (19-18) / (4/√100) = 2,5

Krok 3: Znajdź wartość p statystyki testu Z za pomocą programu Excel.

Aby znaleźć wartość p dla z = 2,5, skorzystamy z następującego wzoru w Excelu: =1 – ROZKŁ.NORMALNY(2,5; 0, 1, PRAWDA)

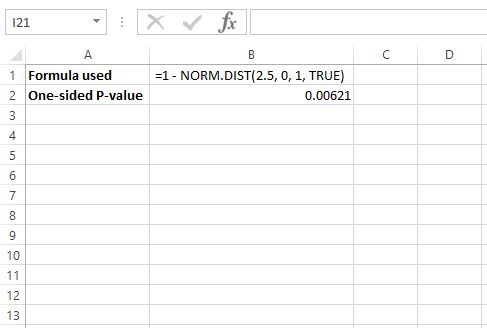
To mówi nam, że jednostronna wartość p wynosi 0,00621 , ale ponieważ przeprowadzamy test dwustronny, musimy pomnożyć tę wartość przez 2, więc wartość p będzie wynosić 0,00612 * 2 = 0,01224 .

Krok 4: Odrzuć lub nie odrzucaj hipotezy zerowej.

Ponieważ wartość p wynosząca 0,01224 jest mniejsza niż wybrany poziom alfa wynoszący 0,05 , odrzucamy hipotezę zerową. Mamy wystarczające dowody, aby stwierdzić, że średnia żywotność nowego akumulatora znacznie różni się od średniej żywotności obecnego standardowego akumulatora.

Przykład 2: Znajdowanie wartości P na podstawie wyniku Z (test jednostronny)

Botanik szacuje, że średnia wysokość określonej rośliny jest mniejsza niż 14 cali. Wybiera losowo 30 roślin i mierzy je. Odkrywa, że średni wzrost wynosi 13,5 cala przy odchyleniu standardowym wynoszącym 2 cale.

Wykonaj jednostronny test hipotezy, używając poziomu alfa 0,01, aby określić, czy średnia wysokość tej rośliny jest w rzeczywistości mniejsza niż 14 cali.

Krok 1: Postaw hipotezy.

Hipoteza zerowa (H0): μ≥ 14

Hipoteza alternatywna: (Ha): μ < 14

Krok 2: Znajdź statystykę testu z.

Statystyka testowa z = (x-μ) / (s/√n) = (13,5-14) / (2/√30) = -1,369

Krok 3: Znajdź wartość p statystyki testu Z za pomocą programu Excel.

Aby znaleźć wartość p dla z = -1,369, użyjemy następującego wzoru w Excelu: = ROZKŁ.NORMALNY(-1,369; 0, 1, PRAWDA)

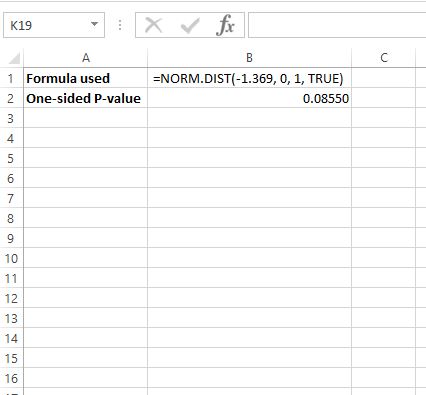
To mówi nam, że jednostronna wartość p wynosi 0,08550 .

Krok 4: Odrzuć lub nie odrzucaj hipotezy zerowej.

Ponieważ wartość p wynosząca 0,08550 jest większa niż wybrany poziom alfa wynoszący 0,01 , nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że średnia wysokość tego gatunku rośliny jest mniejsza niż 14 cali.

Aby uzyskać więcej samouczków na temat statystyk w programie Excel, zapoznaj się z naszą pełną listą przewodników po programie Excel .