Jak wykonać test t dla jednej próby w stata
Test t dla jednej próby służy do sprawdzenia, czy średnia populacji jest równa określonej wartości.
W tym samouczku wyjaśniono, jak wykonać test t dla jednej próbki w Stata.
Przykład: Test t dla jednej próby w Stata
Naukowcy chcą wiedzieć, czy samochody podróżują średnio 20 mil na galon. Pobierają próbkę 74 samochodów i chcą przeprowadzić próbny test T, aby ustalić, czy rzeczywista średnia wartość mpg wynosi 20, czy nie.
Wykonaj poniższe kroki, aby wykonać test t dla jednej próbki.
Krok 1: Załaduj dane.
Najpierw załaduj dane, wpisując use https://www.stata-press.com/data/r13/auto w polu poleceń i klikając Enter.
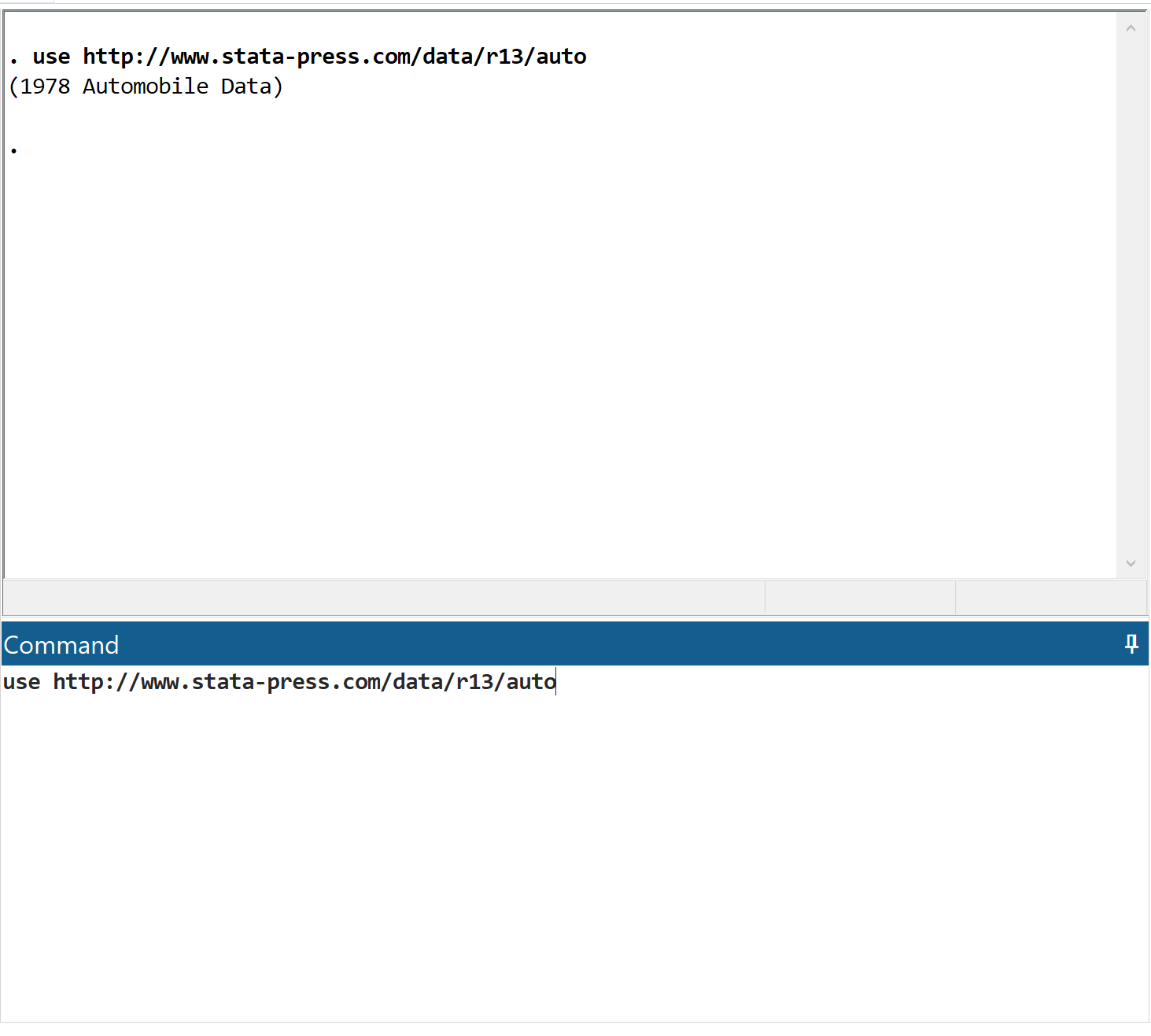
Krok 2: Wyświetl surowe dane.
Przed wykonaniem testu t dla jednej próby przyjrzyjmy się najpierw surowym danym. Z górnego paska menu przejdź do opcji Dane > Edytor danych > Edytor danych (Przeglądaj) . To pokaże nam wiele informacji o każdym z 74 samochodów, ale pamiętaj, że interesują nas tylko mile na galon (kolumna mpg ):
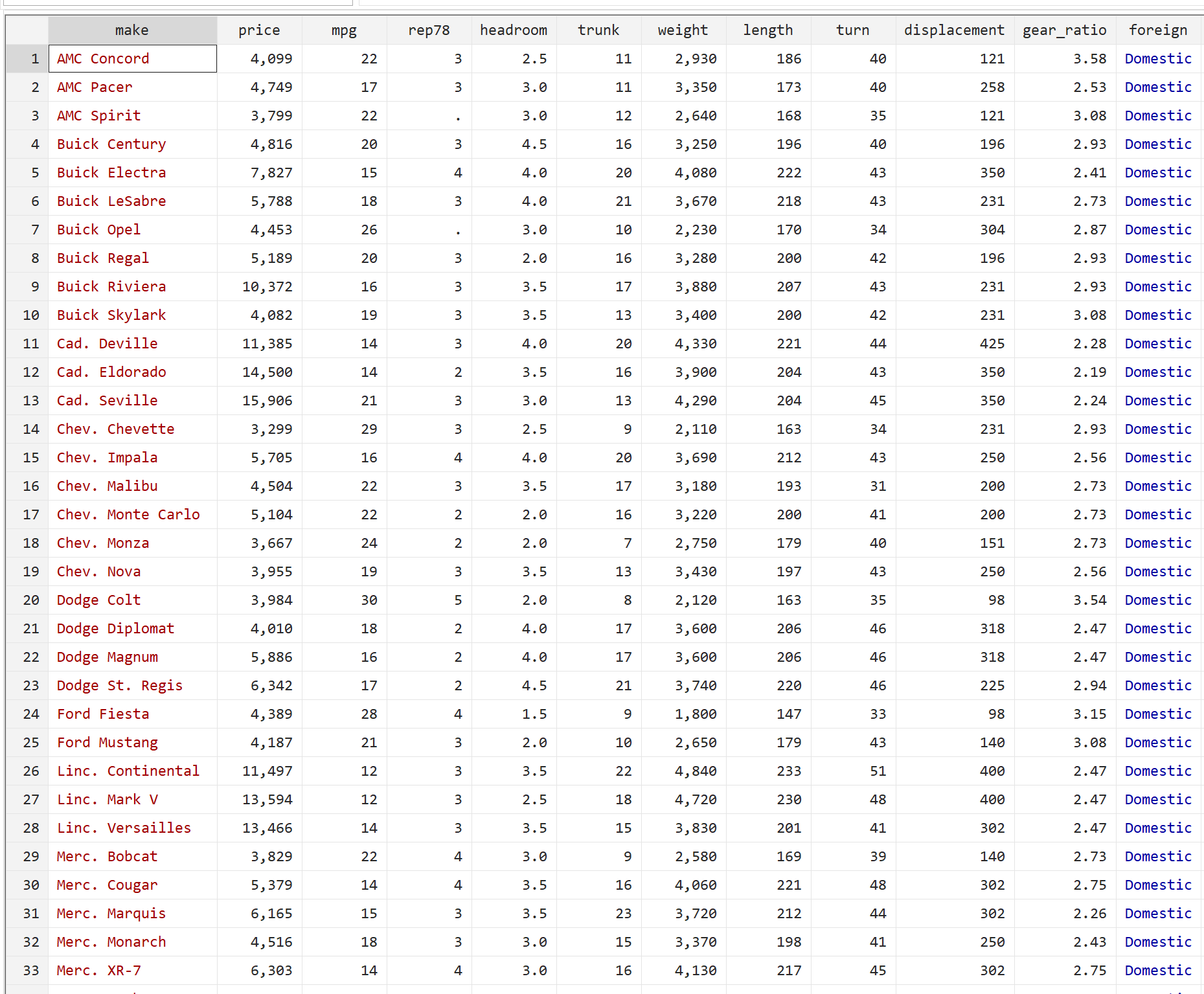
Krok 3: Wykonaj test t dla jednej próbki.
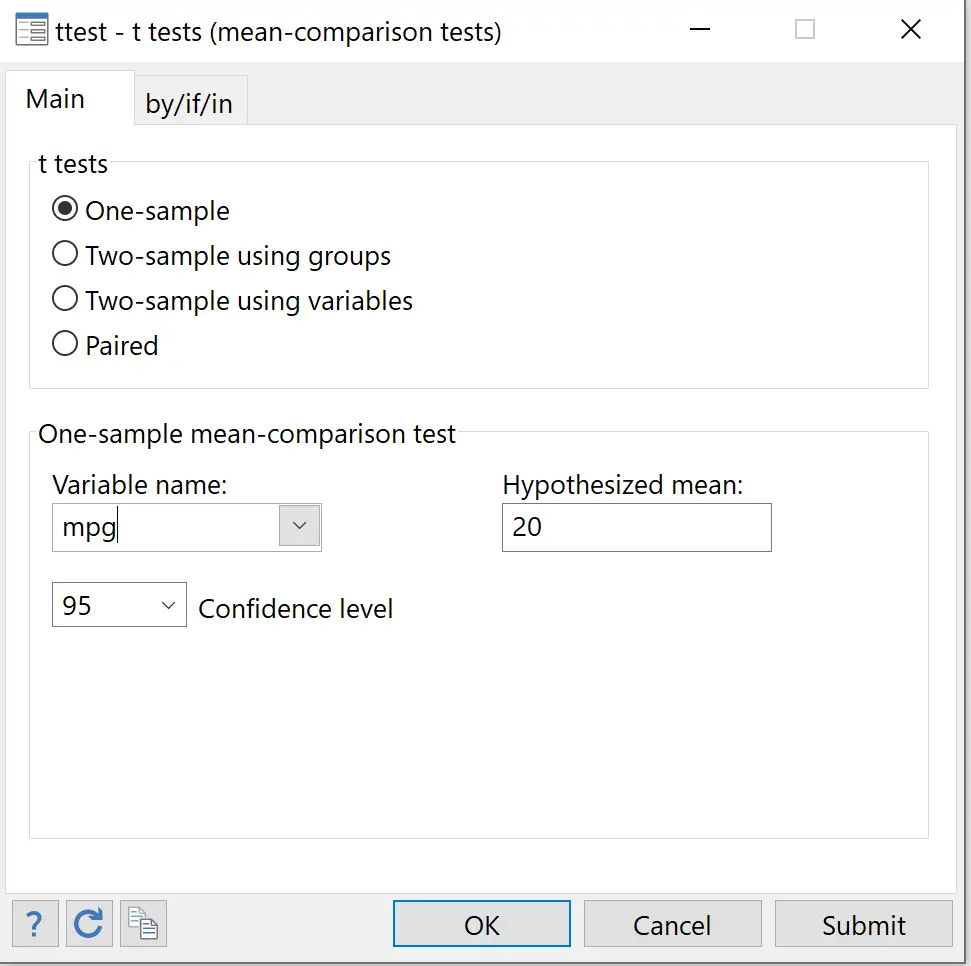
Z górnego paska menu przejdź do Statystyki > Podsumowania, tabele i testy > Klasyczne testy hipotez > Test t (porównanie testu średnich) .
Zachowaj wybraną próbkę . W polu Nazwa zmiennej wybierz mpg . W polu Średnia hipotetyczna wpisz 20 . W obszarze Poziom zaufania wybierz żądany poziom. Wartość 95 odpowiada poziomowi istotności 0,05. Zostawmy to na 95. Na koniec kliknij OK .
Wyświetlone zostaną wyniki testu t dla jednej próbki:

Oto jak interpretować wyniki:
Obs: Liczba obserwacji. W tym przypadku w sumie są 74 samochody.
Średnia: średnia mpg wszystkich samochodów. W tym przypadku średnia wynosi 21,2973 mil na galon.
Standard. Err: obliczono jako σ / √ n = 5,785503 / √ 74 = 0,6725511.
Standard. Dev: odchylenie standardowe mpg. W tym przypadku jest to 5,785503.
95% konf. Interwał: 95% przedział ufności dla prawdziwej średniej populacji.
t: Statystyka testowa, obliczona jako (x – u) / (σ / √n ) = (21,2973-20) / 5,785503 / √74 = 1,9289.
stopnie swobody: stopnie swobody stosowane w teście t, obliczane jako n-1 = 74-1 = 73.
Wartości p dla trzech różnych testów t dla jednej próby pokazano na dole wyników. Ponieważ chcemy zrozumieć, czy prawdziwa średnia mpg wynosi 20, czy nie, przyjrzymy się wynikom testu pośredniego (w którym alternatywną hipotezą jest Ha: średnia !=20), którego wartość p wynosi 0,0576 .
Ponieważ wartość ta nie jest niższa od naszego poziomu istotności wynoszącego 0,05, nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że prawdziwa średnia wartość mpg dla tej populacji samochodów to coś innego niż 20 mpg.
Krok 4: Ogłoś wyniki.
Na koniec podamy wyniki naszego testu t dla jednej próby. Oto przykład, jak to zrobić:
Przeprowadzono test t dla jednej próbki na 74 samochodach, aby ustalić, czy rzeczywista średnia liczba mpg w populacji różni się od 20 mpg.
Wyniki wykazały, że rzeczywista średnia populacji nie różniła się od 20 mpg (t = 1,9289 przy df = 73, p = 0,0576) na poziomie istotności 0,05.
95% przedział ufności dla średniej prawdziwej populacji dał przedział (19,9569, 22,63769).