Klastrowanie k-średnich w pythonie: przykład krok po kroku

Jednym z najpopularniejszych algorytmów grupowania w uczeniu maszynowym jest grupowanie k-średnich .

Grupowanie K-średnich to technika, w której każdą obserwację ze zbioru danych umieszczamy w jednym z K klastrów.

Ostatecznym celem jest utworzenie K klastrów, w których obserwacje w każdym klastrze są do siebie dość podobne, podczas gdy obserwacje w różnych klastrach znacznie się od siebie różnią.

W praktyce do przeprowadzenia grupowania K-średnich stosujemy następujące kroki:

1. Wybierz wartość K.

• Najpierw musimy zdecydować, ile skupień chcemy zidentyfikować w danych. Często wystarczy po prostu przetestować kilka różnych wartości K i przeanalizować wyniki, aby zobaczyć, która liczba skupień wydaje się mieć największy sens dla danego problemu.

2. Losowo przypisz każdą obserwację do skupienia początkowego, od 1 do K.

3. Wykonuj poniższą procedurę, aż przypisania klastrów przestaną się zmieniać.

• Dla każdej z gromad K oblicz środek ciężkości gromady. Jest to po prostu wektor p- średnich cech obserwacji k-tego klastra.
• Przypisz każdą obserwację do klastra o najbliższym centroidzie. Tutaj najbliżej definiuje się odległość euklidesową .

Poniższy przykład pokazuje krok po kroku, jak wykonać grupowanie k-średnich w Pythonie przy użyciu funkcji KMeans z modułu sklearn .

Krok 1: Zaimportuj niezbędne moduły

Najpierw zaimportujemy wszystkie moduły potrzebne do wykonania grupowania k-średnich:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Krok 2: Utwórz ramkę danych

Następnie utworzymy DataFrame zawierającą następujące trzy zmienne dla 20 różnych koszykarzy:

• zwrotnica
• pomoc
• odbija się

Poniższy kod pokazuje, jak utworzyć tę ramkę DataFrame pand:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#view first five rows of DataFrame
print ( df.head ())

   points assists rebounds
0 18.0 3.0 15
1 NaN 3.0 14
2 19.0 4.0 14
3 14.0 5.0 10
4 14.0 4.0 8

Będziemy używać grupowania k-średnich do grupowania podobnych aktorów w oparciu o te trzy metryki.

Krok 3: Oczyść i przygotuj ramkę DataFrame

Następnie wykonamy następujące kroki:

• Użyj dropna() , aby upuścić wiersze z wartościami NaN w dowolnej kolumnie
• Użyj StandardScaler() , aby przeskalować każdą zmienną tak, aby miała średnią 0 i odchylenie standardowe 1.

Poniższy kod pokazuje, jak to zrobić:

 #drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

#view first five rows of scaled DataFrame
print (scaled_df[:5])

[[-0.86660275 -1.22683918 1.72722524]
 [-0.72081911 -0.96077767 1.45687694]
 [-1.44973731 -0.69471616 0.37548375]
 [-1.44973731 -0.96077767 -0.16521285]
 [-1.88708823 -0.16259314 1.45687694]]

Uwaga : Stosujemy skalowanie, aby każda zmienna miała takie samo znaczenie podczas dopasowywania algorytmu k-średnich. W przeciwnym razie zmienne o najszerszych zakresach miałyby zbyt duży wpływ.

Krok 4: Znajdź optymalną liczbę skupień

Aby wykonać grupowanie k-średnich w Pythonie, możemy użyć funkcji KMeans z modułu sklearn .

Ta funkcja wykorzystuje następującą podstawową składnię:

KMeans(init=’random’, n_clusters=8, n_init=10, random_state=None)

Złoto:

• init : Kontroluje technikę inicjalizacji.
• n_clusters : liczba klastrów, w których należy umieścić obserwacje.
• n_init : Liczba inicjalizacji do wykonania. Domyślnie uruchamiany jest algorytm k-średnich 10 razy i zwracany jest ten z najniższym SSE.
• random_state : Wartość całkowita, którą możesz wybrać, aby wyniki algorytmu były powtarzalne.

Najważniejszym argumentem tej funkcji jest n_clusters, który określa, w ilu klastrach należy umieścić obserwacje.

Nie wiemy jednak z góry, ile skupień jest optymalnych, dlatego musimy stworzyć wykres przedstawiający liczbę skupień oraz SSE (suma kwadratów błędów) modelu.

Zazwyczaj, tworząc tego typu wykres, szukamy „kolana”, w którym suma kwadratów zaczyna się „zaginać” lub wyrównywać. Jest to na ogół optymalna liczba klastrów.

Poniższy kod pokazuje, jak utworzyć tego typu wykres, który wyświetla liczbę skupień na osi x i SSE na osi y:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

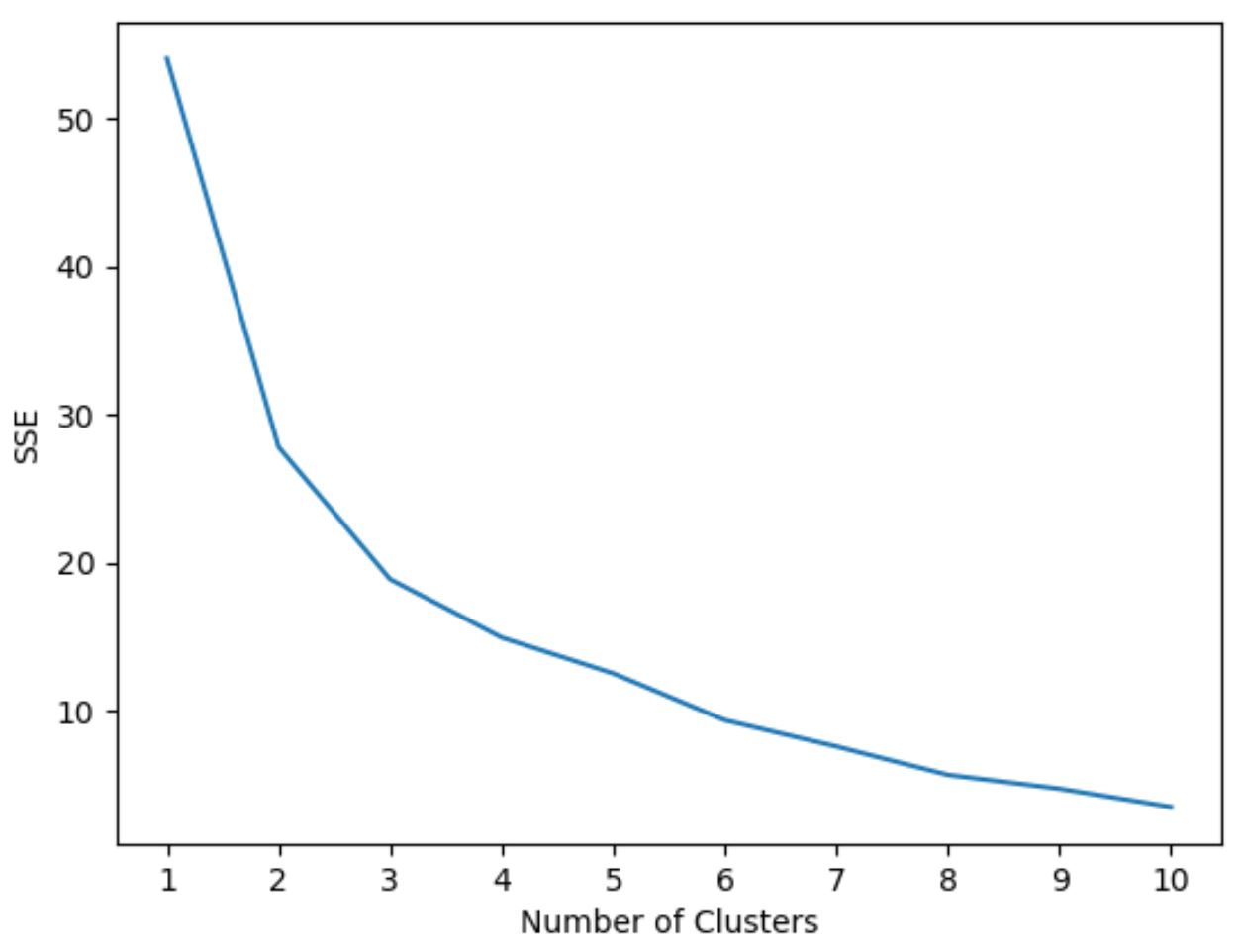
Na tym wykresie wydaje się, że w k = 3 skupiskach występuje załamanie lub „kolano”.

Zatem w następnym kroku podczas dopasowywania naszego modelu grupowania k-średnich użyjemy 3 klastrów.

Uwaga : w świecie rzeczywistym zaleca się użycie kombinacji tego wykresu i wiedzy specjalistycznej w dziedzinie, aby wybrać liczbę używanych klastrów.

Krok 5: Wykonaj grupowanie K-średnich z optymalnym K

Poniższy kod pokazuje, jak wykonać grupowanie k-średnich na zbiorze danych przy użyciu optymalnej wartości k z 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

Wynikowa tabela przedstawia przypisania klastrów dla każdej obserwacji w ramce DataFrame.

Aby ułatwić interpretację tych wyników, możemy dodać kolumnę do DataFrame, która pokazuje przypisanie każdego gracza do klastra:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

Kolumna klastra zawiera numer klastra (0, 1 lub 2), do którego przypisano każdego gracza.

Zawodnicy należący do tego samego klastra mają w przybliżeniu podobne wartości w kolumnach punktów , asyst i zbiórek .

Uwaga : Pełną dokumentację funkcji KMeans sklearna znajdziesz tutaj .

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe zadania w Pythonie:

Jak wykonać regresję liniową w Pythonie
Jak przeprowadzić regresję logistyczną w Pythonie
Jak przeprowadzić weryfikację krzyżową K-Fold w Pythonie