Jak obliczyć współczynnik korelacji na kalkulatorze ti-84
Współczynnik korelacji jest miarą liniowego powiązania między dwiema zmiennymi. Może przyjmować wartość z zakresu od -1 do 1, gdzie:
- -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
- Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
- 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi
Aby obliczyć współczynnik korelacji między dwiema zmiennymi na kalkulatorze TI-84, można wykonać następujące kroki:
Krok 1: Włącz diagnostykę.
Najpierw musimy włączyć diagnostykę. Aby to zrobić, naciśnij 2 , a następnie naciśnij cyfrę 0. Spowoduje to przejście do ekranu KATALOG.

Przewiń do DiagnosticOn i naciśnij ENTER .
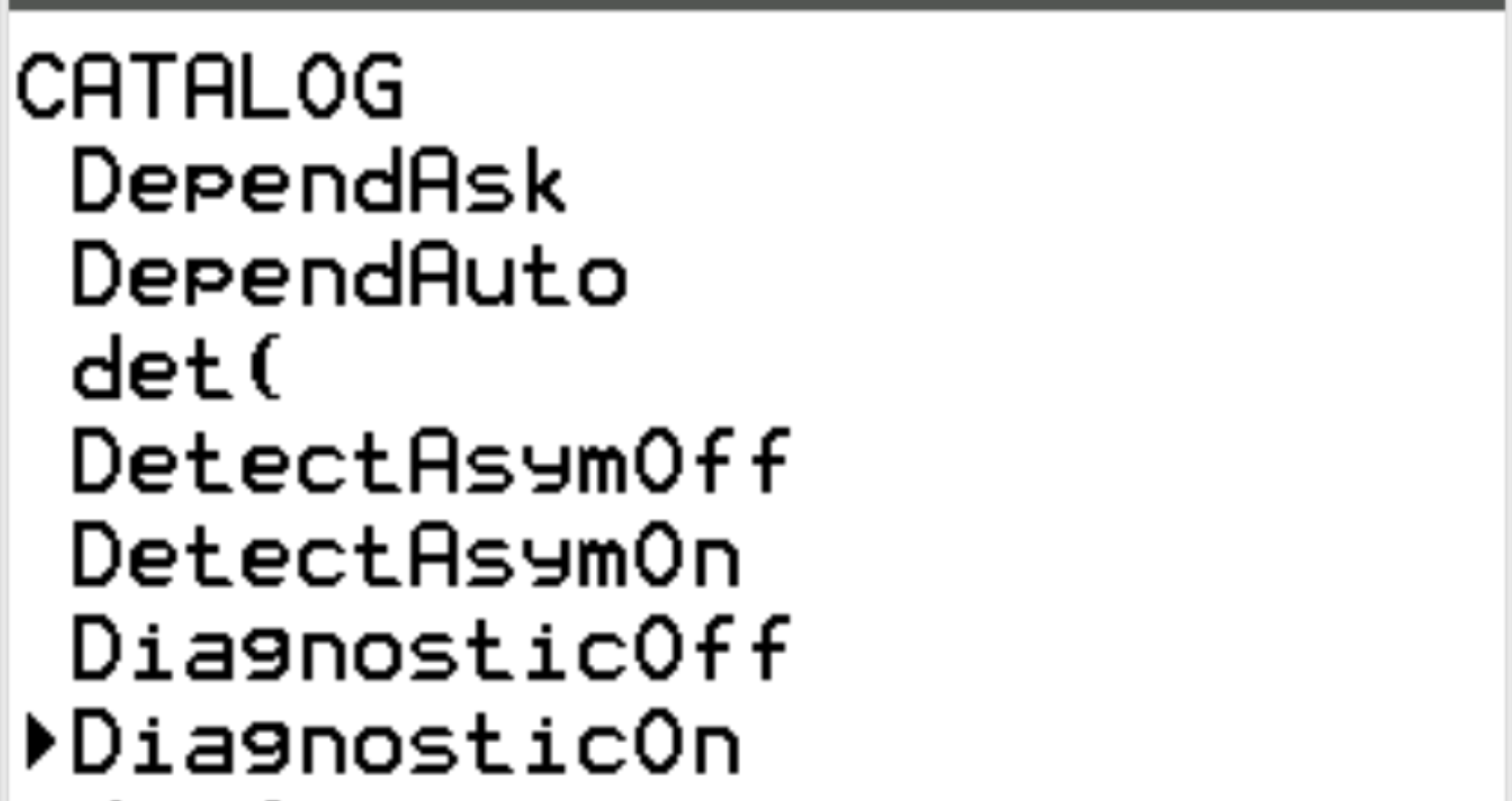
Następnie naciśnij ponownie ENTER .
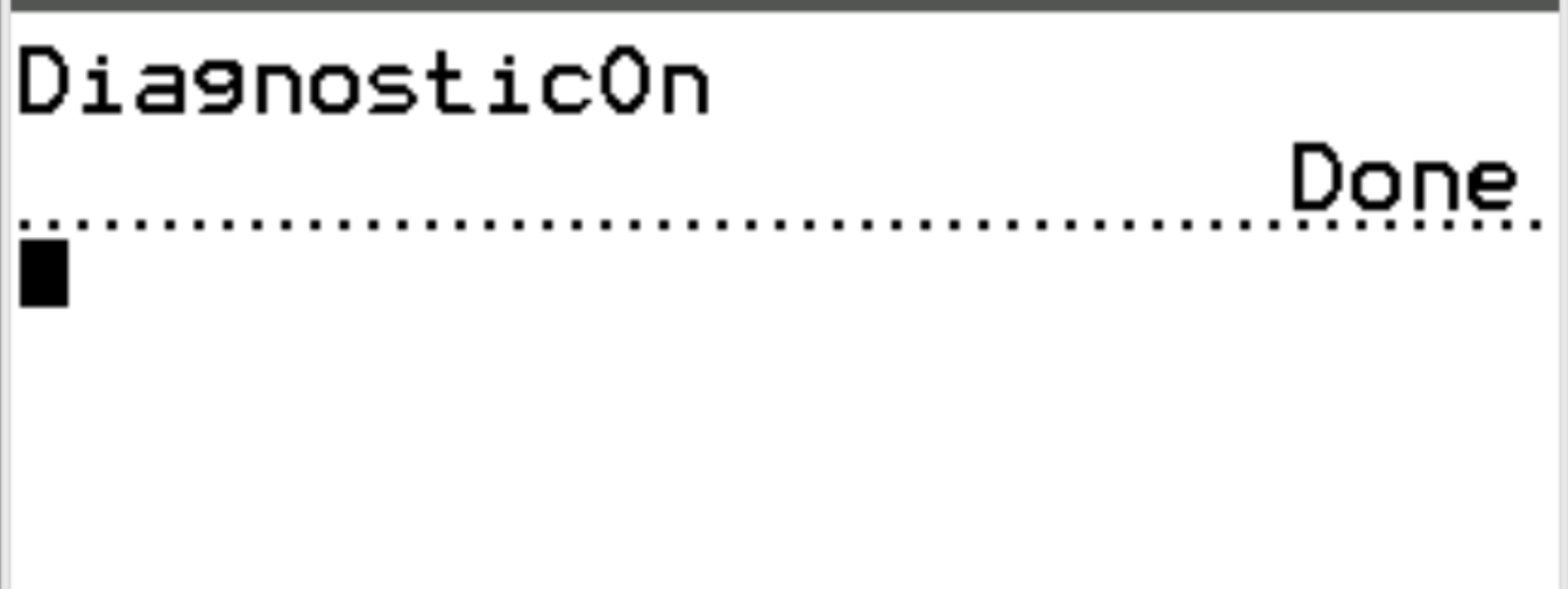
Diagnostyka jest teraz włączona, dzięki czemu możemy obliczyć współczynnik korelacji między dwiema zmiennymi.
Krok 2: Wprowadź dane.
Następnie musimy wprowadzić wartości danych dla naszych dwóch zmiennych. Naciśnij Stat , następnie naciśnij EDYTUJ . Wpisz wartości pierwszej zmiennej w kolumnie L1 i wartości drugiej zmiennej w kolumnie L2:
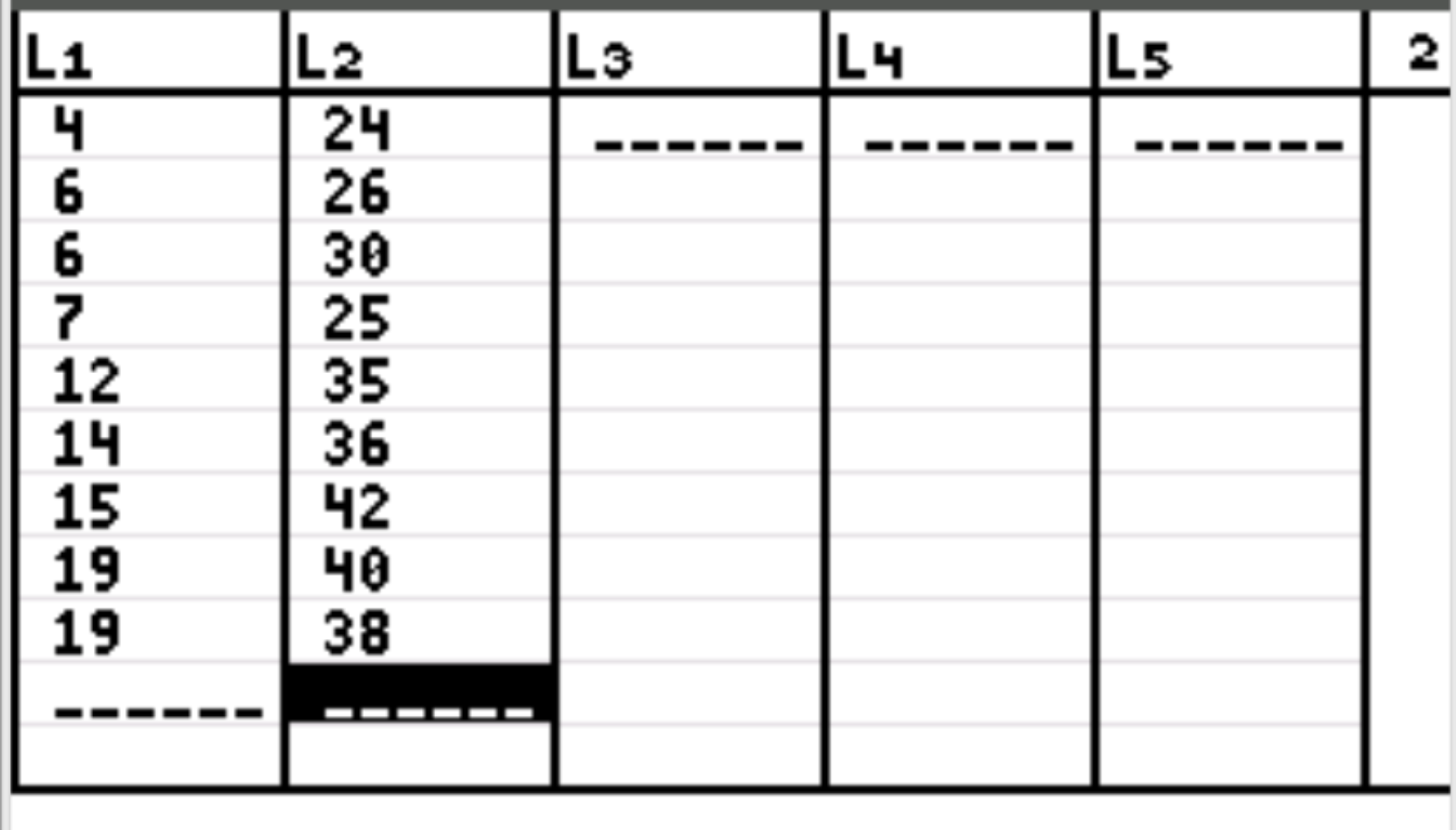
Krok 3: Znajdź współczynnik korelacji.
Następnie obliczymy współczynnik korelacji pomiędzy obiema zmiennymi. Naciśnij Stat, a następnie przewiń do CALC . Następnie przewiń do 8: Linreg(a+bx) i naciśnij Enter .
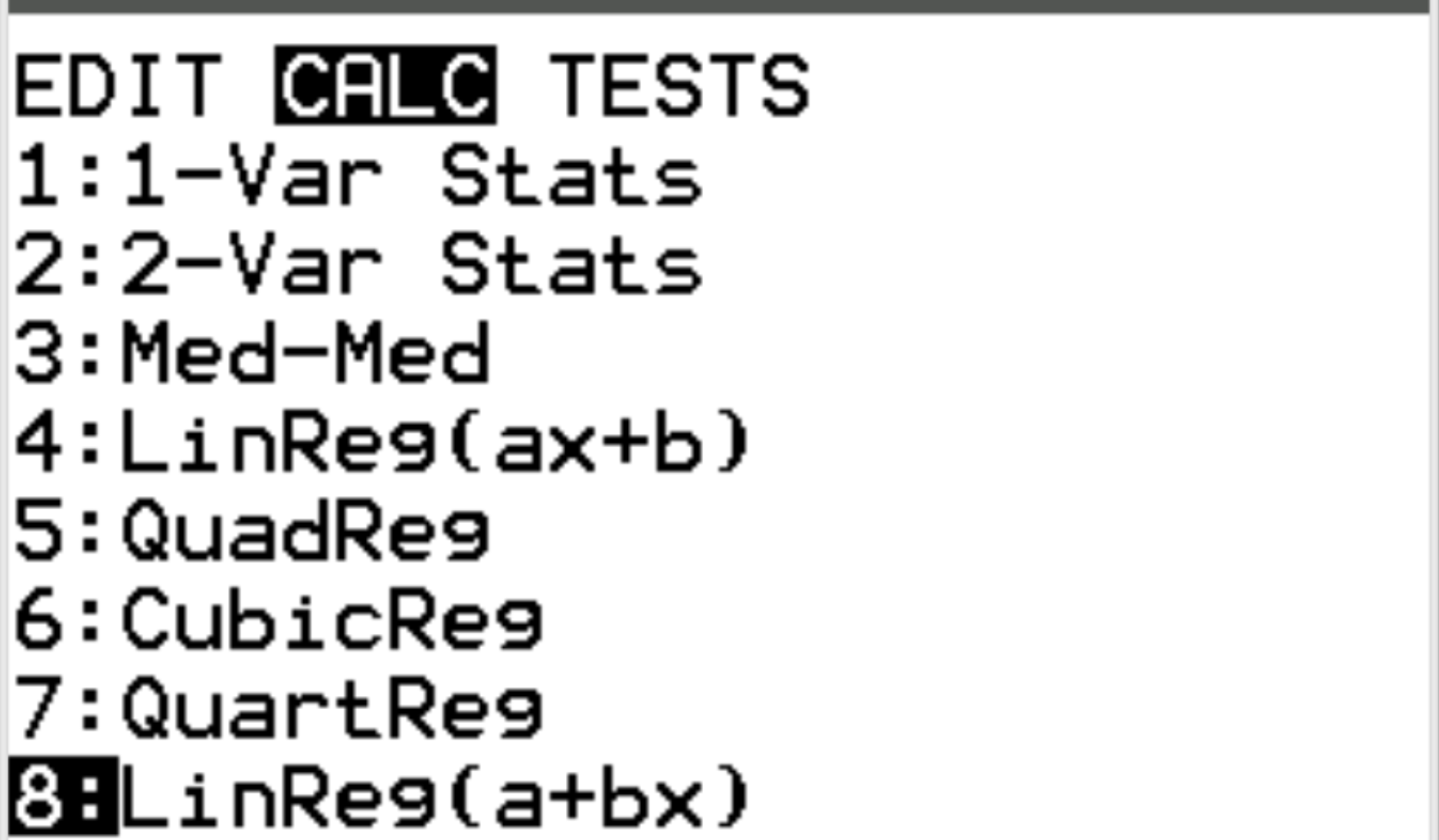
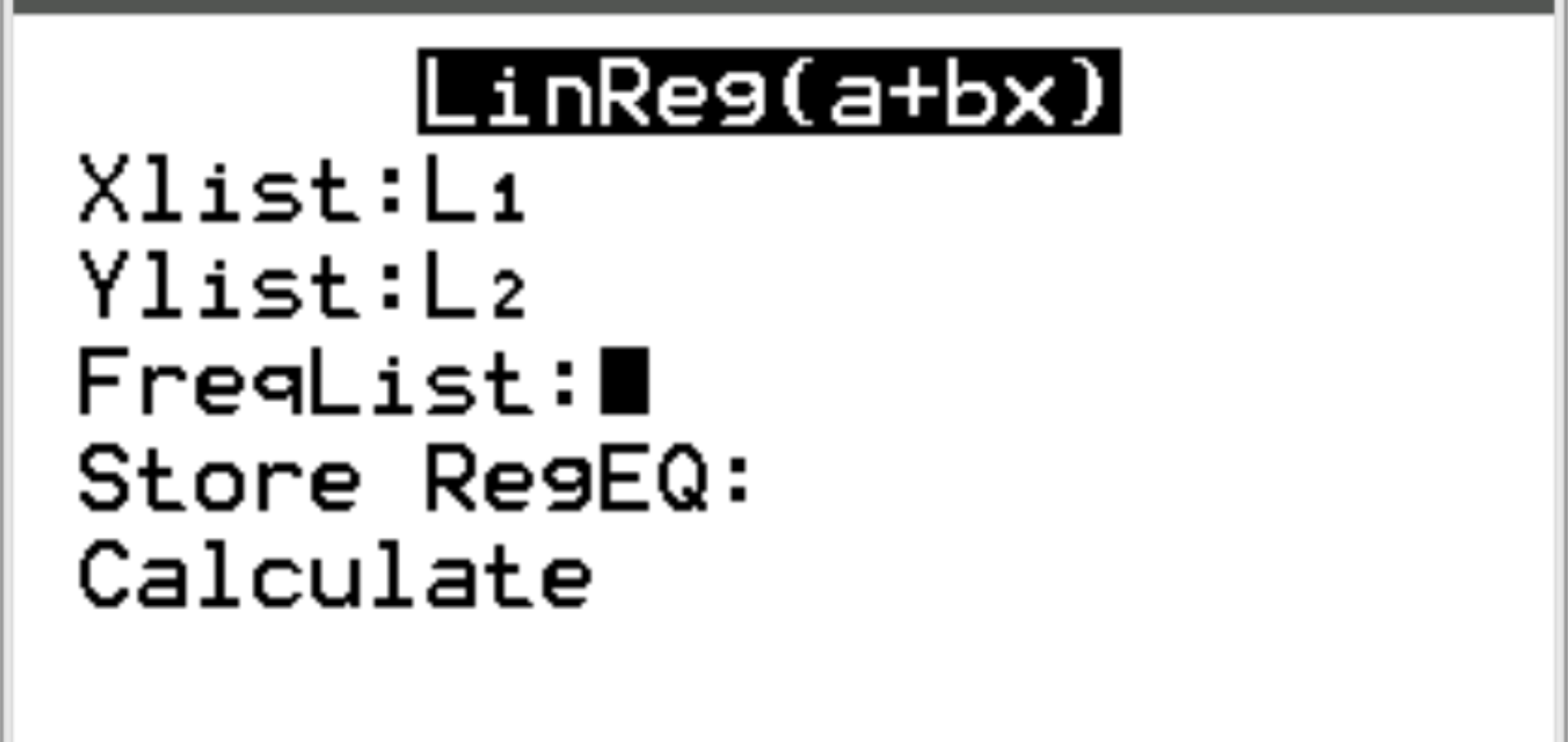
W przypadku Xlist i Ylist upewnij się, że wybrano L1 i L2, ponieważ są to kolumny, których użyliśmy do wprowadzenia naszych danych. Pozostaw listę FreqList pustą. Przewiń w dół do Oblicz i naciśnij Enter .
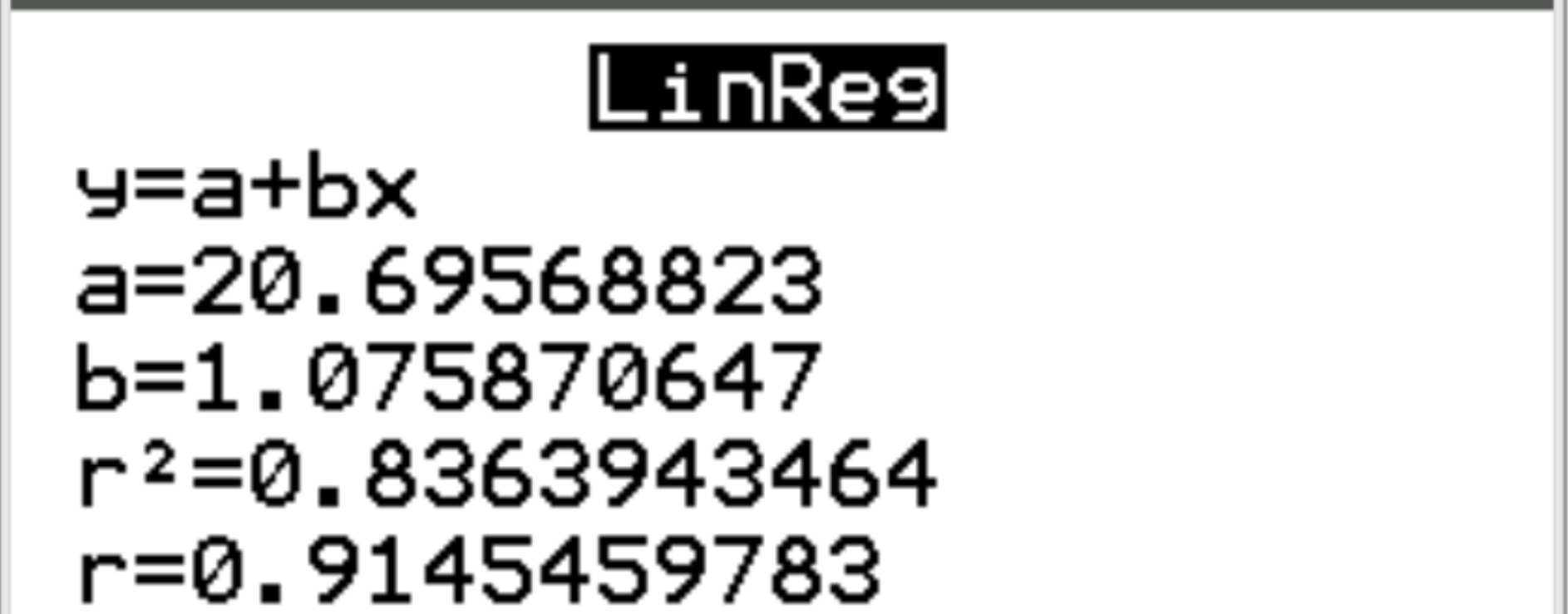
Na nowym ekranie widzimy, że współczynnik korelacji (r) pomiędzy obiema zmiennymi wynosi 0,9145 .
Jak interpretować współczynnik korelacji
Poniższa tabela przedstawia praktyczną zasadę interpretacji siły związku między dwiema zmiennymi w oparciu o wartość r :
| Wartość bezwzględna r | Siła związku |
|---|---|
| r < 0,25 | Brak relacji |
| 0,25 < r < 0,5 | Słaby związek |
| 0,5 < r < 0,75 | Umiarkowane relacje |
| r > 0,75 | Silny związek |
W naszym przykładzie współczynnik korelacji wynoszący 0,9145 wskazuje na silną dodatnią zależność pomiędzy obiema zmiennymi.