Karta kontrolna u

W tym artykule wyjaśniamy, czym jest karta kontrolna U, jakie są jej cechy i do czego służy. Dodatkowo będziesz mógł zobaczyć jak powstaje wykres kontrolny U i krok po kroku rozwiązane ćwiczenie.

Co to jest karta kontrolna U?

Wykres kontrolny U lub po prostu wykres U to wykres przedstawiający liczbę wystąpień zjawiska na jednostkę miary, jeśli jest ona zmienna.

Na przykład kartę kontrolną U można wykorzystać do kontrolowania liczby defektów na metr kwadratowy tkaniny. Często nie można pobrać próbek tkanin o tej samej powierzchni, dlatego każda próbka jest inna. Zatem wykres U pozwala nam badać procesy, które mają różną wielkość próby.

Należy zauważyć, że wykres kontrolny U nie przedstawia liczby wadliwych jednostek, ale liczbę defektów, jakie ma każda jednostka, jak na wykresie C. Natomiast karta kontrolna P lub NP kontroluje proporcję i liczbę wadliwych produktów. Poniżej przyjrzymy się różnicom pomiędzy wszystkimi typami kart kontrolnych.

Należy pamiętać, że referencyjnym modelem matematycznym wykresu kontrolnego U jest rozkład Poissona, ponieważ badamy liczbę wystąpień zjawiska na jednostkę miary.

Jak utworzyć wykres kontrolny U

Teraz, gdy znamy już definicję karty kontrolnej U, przyjrzyjmy się, jak powstaje tego typu wykres kontrolny:

1. Pobieranie próbek : po pierwsze należy pobrać różne próbki, aby zobaczyć ewolucję mierzonego zjawiska. Próbki muszą być tej samej wielkości, dodatkowo zaleca się pobranie minimum 20 próbek.
2. Określ, ile razy dane zjawisko występuje na jednostkę miary : dla każdej próbki ile razy badane zjawisko się powtarza.
3. Oblicz średnią wartość wystąpień : na podstawie zebranych danych należy obliczyć średnią częstości występowania zjawiska na jednostkę miary.



4. Oblicz limity kontrolne U-Card – Następnie należy obliczyć limity kontrolne U-Card, korzystając ze wzorów podanych poniżej. Należy pamiętać, że wartość granic kontrolnych różni się w zależności od wielkości próby.





Złoto



I



są odpowiednio górną i dolną granicą kontrolną próbki i,



jest średnią wartością wystąpień i



to wielkość próbki, tj.

5. Nanoszenie wartości na mapę – Zebrane wartości wraz z obliczonymi granicami kontrolnymi należy teraz nanieść na mapę, aby utworzyć kartę kontrolną U.
6. Przeanalizuj kartę kontrolną U : ostatecznie pozostaje tylko sprawdzić, czy żadna wartość na karcie nie wykracza poza granice kontrolne, a zatem czy proces jest pod kontrolą. W przeciwnym razie należy podjąć działania w celu skorygowania procesu.

Przykład karty sterującej U

• Przedsiębiorstwo przemysłowe chce kontrolować liczbę defektów na ^m2 tkaniny. Poniższa tabela przedstawia poddane analizie próbki oraz liczbę stwierdzonych wad. Utwórz kartę kontrolną U, aby zbadać liczbę defektów.

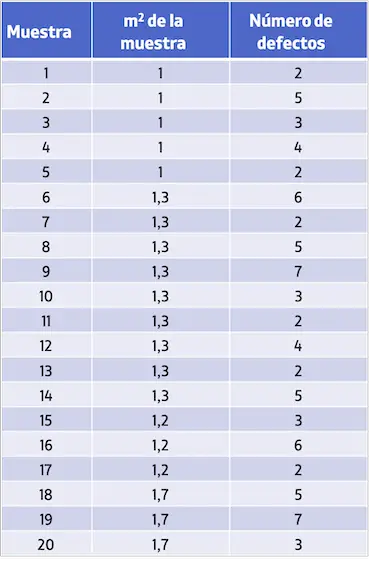
Aby utworzyć kartę kontrolną U, należy najpierw obliczyć średnią wartość liczby defektów na próbkę:

Teraz musimy obliczyć granice kontrolne dla każdej próbki. Przykładowo, poniżej obliczono granice kontrolne dla pierwszej próbki:

Wszystkie dolne granice kontrolne dają liczbę ujemną, co nie ma sensu. Dlatego ustalimy dolne granice kontrolne na 0.

Zatem wartości granic kontrolnych dla każdej próbki są następujące:

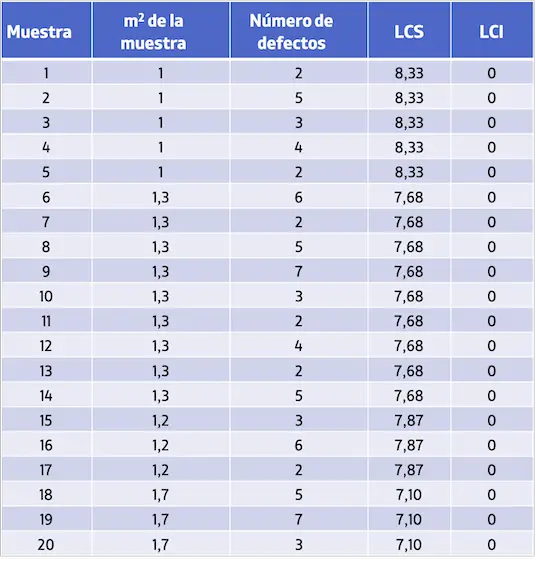
Na koniec wystarczy przedstawić wszystkie wartości na wykresie, aby otrzymać kartę kontrolną U:

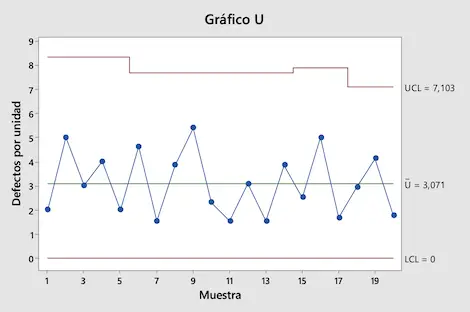
Jak widać na wykonanym przez nas wykresie U, wszystkie wartości mieszczą się w granicach kontrolnych. Można zatem stwierdzić, że proces produkcyjny jest pod kontrolą.

Inne typy wykresów kontrolnych

Oprócz wykresu U istnieją inne typy wykresów kontroli atrybutów:

• Karta kontrolna P : kontrolowana jest proporcja wadliwych produktów.
• Karta kontrolna NP : kontrolowana jest liczba wadliwych produktów.
• Wykres kontrolny C : Kontroluje się liczbę defektów jak na wykresie U, ale wielkość próbki jest stała.