Kiedy warto zastosować korelację? (wyjaśnienie i przykłady)

Korelację stosuje się do pomiaru liniowego powiązania między dwiema zmiennymi.

Współczynnik korelacji zawsze przyjmuje wartość od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Pytanie, które często zadają uczniowie, brzmi: Kiedy powinienem używać korelacji?

Krótka odpowiedź: użyj korelacji, jeśli chcesz określić liniową zależność między dwiema zmiennymi, a żadna ze zmiennych nie reprezentuje zmiennej odpowiedzi lub „wyniku” .

Poniższe przykłady ilustrują, kiedy należy, a kiedy nie należy stosować korelacji w praktyce.

Przykład 1: Kiedy stosować korelację

Załóżmy, że profesor chce zrozumieć liniową zależność między wynikami testów z matematyki a wynikami uczniów w testach z przedmiotów ścisłych i przyrodniczych.

Na przykład, czy uczniowie, którzy dobrze radzą sobie na egzaminie z matematyki, radzą sobie również dobrze na egzaminie z przedmiotów ścisłych? A może uczniowie, którzy osiągają wysokie wyniki w matematyce, zwykle osiągają niskie wyniki w przedmiotach ścisłych?

W tym scenariuszu mógłby obliczyć korelację między wynikami egzaminów z matematyki a wynikami egzaminów z przedmiotów ścisłych i przyrodniczych, ponieważ chce po prostu zrozumieć liniową zależność między tymi dwiema zmiennymi, a żadnej ze zmiennych nie można uznać za zmienną odpowiedzi.

Załóżmy, że oblicza współczynnik korelacji Pearsona i stwierdza, że wynosi on r = 0,78. Jest to silna dodatnia korelacja, co oznacza, że uczniowie, którzy osiągają dobre wyniki w matematyce, zwykle osiągają dobre wyniki w naukach ścisłych.

Przykład 2: Kiedy nie stosować korelacji

Załóżmy, że dział marketingu firmy chce określić ilościowo wpływ wydatków na reklamę na całkowite przychody.

Na przykład, ile dodatkowych przychodów może spodziewać się firma za każdego dodatkowego dolara wydanego na reklamę?

W tym scenariuszu dział musi zastosować model regresji liniowej , aby określić ilościowo związek między wydatkami na reklamę a całkowitymi przychodami, ponieważ zmienna „przychody” jest zmienną odpowiedzi.

Załóżmy, że dział stosuje prosty model regresji liniowej i stwierdza, że poniższe równanie najlepiej opisuje związek między wydatkami na reklamę a całkowitymi przychodami:

Przychody ogółem = 145,4 + 0,34*(wydatki na reklamę)

Zinterpretowalibyśmy to w ten sposób, że każdy dodatkowy dolar wydany na reklamę powoduje średni wzrost całkowitego przychodu o średnio 0,34 dolara.

Środki ostrożności dotyczące stosowania korelacji

Należy zauważyć, że korelację można zastosować jedynie do ilościowego określenia liniowej zależności między dwiema zmiennymi.

Jednakże w pewnych okolicznościach współczynnik korelacji nie będzie w stanie skutecznie uchwycić związku między dwiema zmiennymi, których związek jest nieliniowy.

Załóżmy na przykład, że tworzymy następujący wykres rozrzutu, aby zwizualizować związek między dwiema zmiennymi:

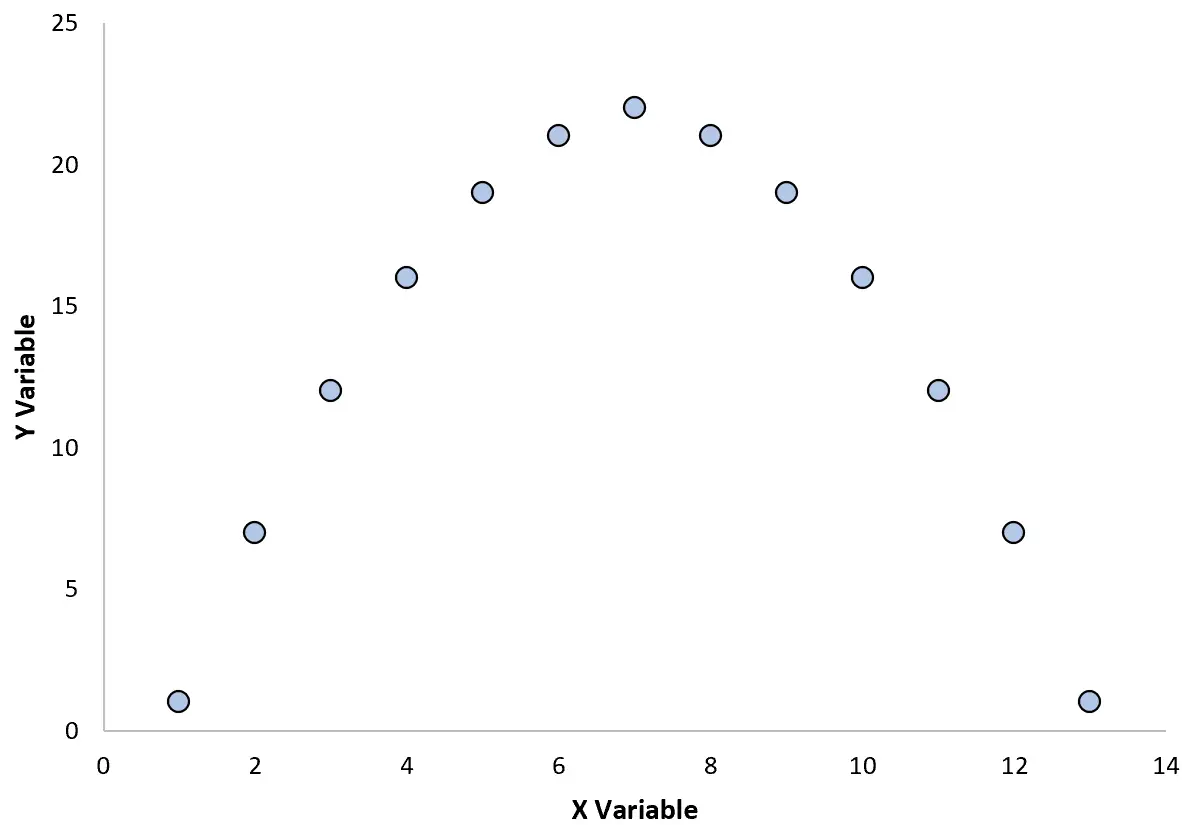
Jeżeli obliczymy współczynnik korelacji pomiędzy tymi dwiema zmiennymi, okaże się, że wynosi on r = 0. Oznacza to, że pomiędzy obiema zmiennymi nie ma liniowej zależności.

Jednakże z wykresu widać, że pomiędzy tymi dwiema zmiennymi rzeczywiście istnieje związek – jest to po prostu zależność kwadratowa, a nie liniowa.

Zatem obliczając korelację między dwiema zmiennymi należy pamiętać, że przydatne może być również utworzenie wykresu rozrzutu w celu wizualizacji związku między zmiennymi.

Nawet jeśli dwie zmienne nie są ze sobą powiązane liniowo, możliwe jest, że istnieje między nimi związek nieliniowy, który zostanie ujawniony na wykresie rozrzutu.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają bardziej szczegółowo, w jaki sposób korelacja jest wykorzystywana w różnych okolicznościach:

6 przykładów korelacji z życia wziętych
Co uważa się za „silną” korelację?
Korelacja vs. skojarzenie: jaka jest różnica?
Korelacja a regresja: jaka jest różnica?