Kiedy stosować korelację rang spearmana (2 scenariusze)

Najbardziej powszechnym sposobem ilościowego określenia liniowego powiązania między dwiema zmiennymi jest użycie współczynnika korelacji Pearsona , który zawsze przyjmuje wartość z zakresu od -1 do 1, gdzie:

• -1 oznacza doskonale ujemną korelację liniową
• Wartość 0 oznacza brak korelacji liniowej
• 1 wskazuje doskonale dodatnią korelację liniową

Jednakże ten typ współczynnika korelacji działa najlepiej, gdy prawdziwa zależność między dwiema zmiennymi jest liniowa .

Istnieje inny typ współczynnika korelacji, zwany korelacją rang Spearmana , który najlepiej stosować w dwóch konkretnych scenariuszach:

Scenariusz 1 : Podczas pracy z tajnymi danymi.

• Przykładem może być zbiór danych zawierający ranking wyników ucznia z egzaminu z matematyki, a także ranking jego wyników z egzaminu z przedmiotów ścisłych w klasie.

Scenariusz 2 : gdy występuje co najmniej jedna skrajna wartość odstająca.

• Kiedy w zbiorze danych występują skrajne wartości odstające, współczynnik korelacji Pearsona jest w dużym stopniu zmieniony.

Poniższe przykłady pokazują, jak obliczyć korelację rang Spearmana w każdym z tych scenariuszy.

Scenariusz 1: Korelacja rankingu włóczników z danymi rankingowymi

Rozważ następujący zbiór danych (i odpowiadający mu wykres rozrzutu), który pokazuje związek między dwiema zmiennymi:

Korzystając z oprogramowania statystycznego, możemy obliczyć następujące współczynniki korelacji dla tych dwóch zmiennych:

• Korelacja Pearsona: 0,79
• Korelacja rang Spearmana: 1

W tym scenariuszu, jeśli zależy nam tylko na randze wartości danych (w miarę wzrostu rangi x, czy ranga y również wzrasta?), to korelacja rang Spearmana dałaby nam lepszy obraz korelację pomiędzy obiema zmiennymi. .

W tym konkretnym zbiorze danych, wraz ze wzrostem rangi x, ranga y zawsze wzrasta.

Korelacja rang Spearmana doskonale oddaje to zachowanie, mówiąc nam, że istnieje doskonały dodatni związek ( ρ = 1 ) pomiędzy rzędami x i rzędami y.

Z drugiej strony korelacja Pearsona mówi nam, że istnieje silna zależność liniowa ( r = 0,79 ) pomiędzy obiema zmiennymi.

To prawda, ale nie jest to przydatne, jeśli interesuje nas tylko relacja między rzędami x i rzędami y.

Scenariusz 2: Korelacja rankingu Spearmana ze skrajnymi wartościami odstającymi

Rozważ następujący zbiór danych (i odpowiadający mu wykres rozrzutu), który pokazuje związek między dwiema zmiennymi:

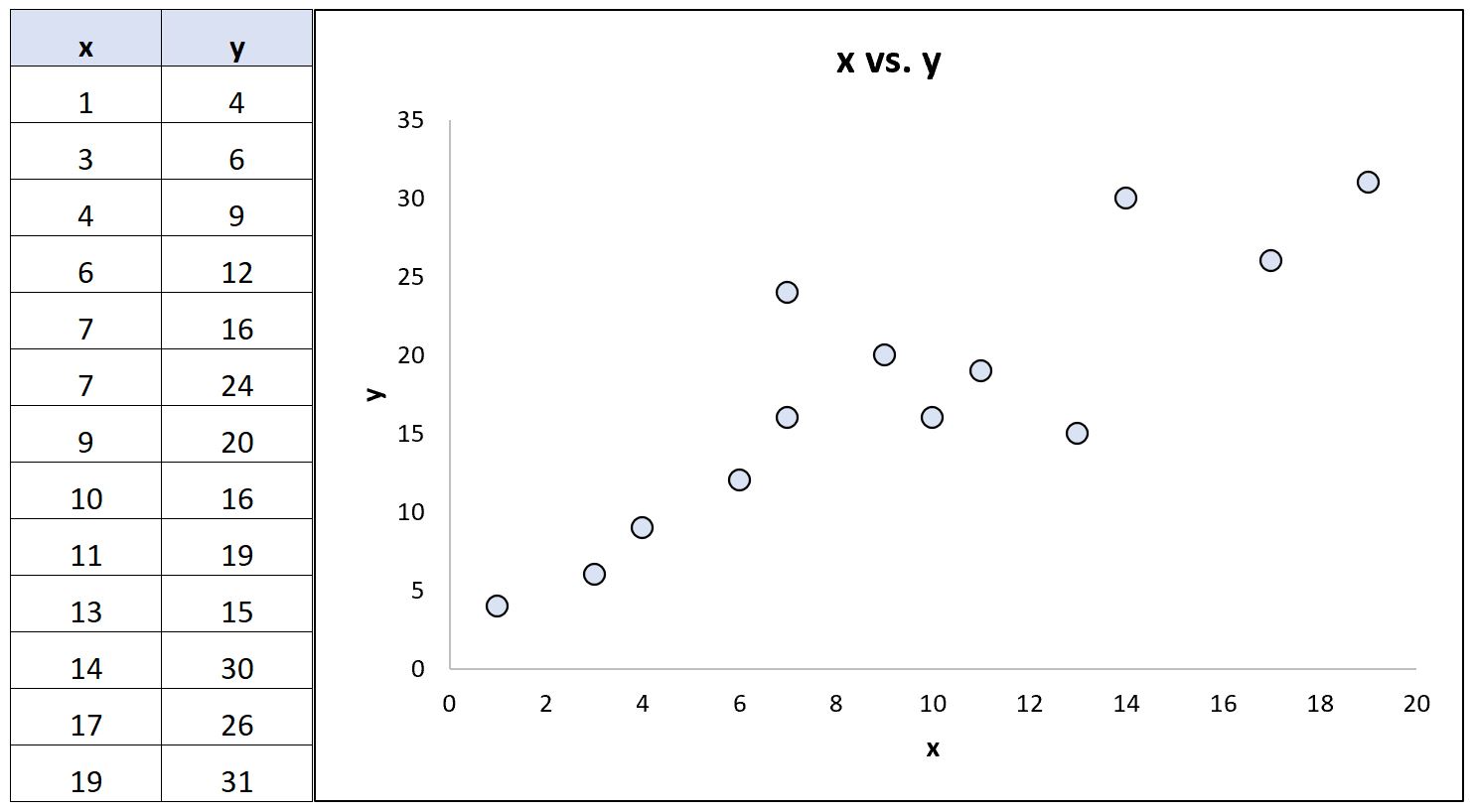
Korzystając z oprogramowania statystycznego, możemy obliczyć następujące współczynniki korelacji dla tych dwóch zmiennych:

• Korelacja Pearsona: 0,86
• Korelacja rangi Spearmana: 0,85

Współczynniki korelacji są prawie identyczne, ponieważ podstawowa zależność między zmiennymi jest w przybliżeniu liniowa i nie ma skrajnych wartości odstających.

Załóżmy teraz, że zmienimy ostatnią wartość y w zbiorze danych, tak że stanie się ona skrajną wartością odstającą:

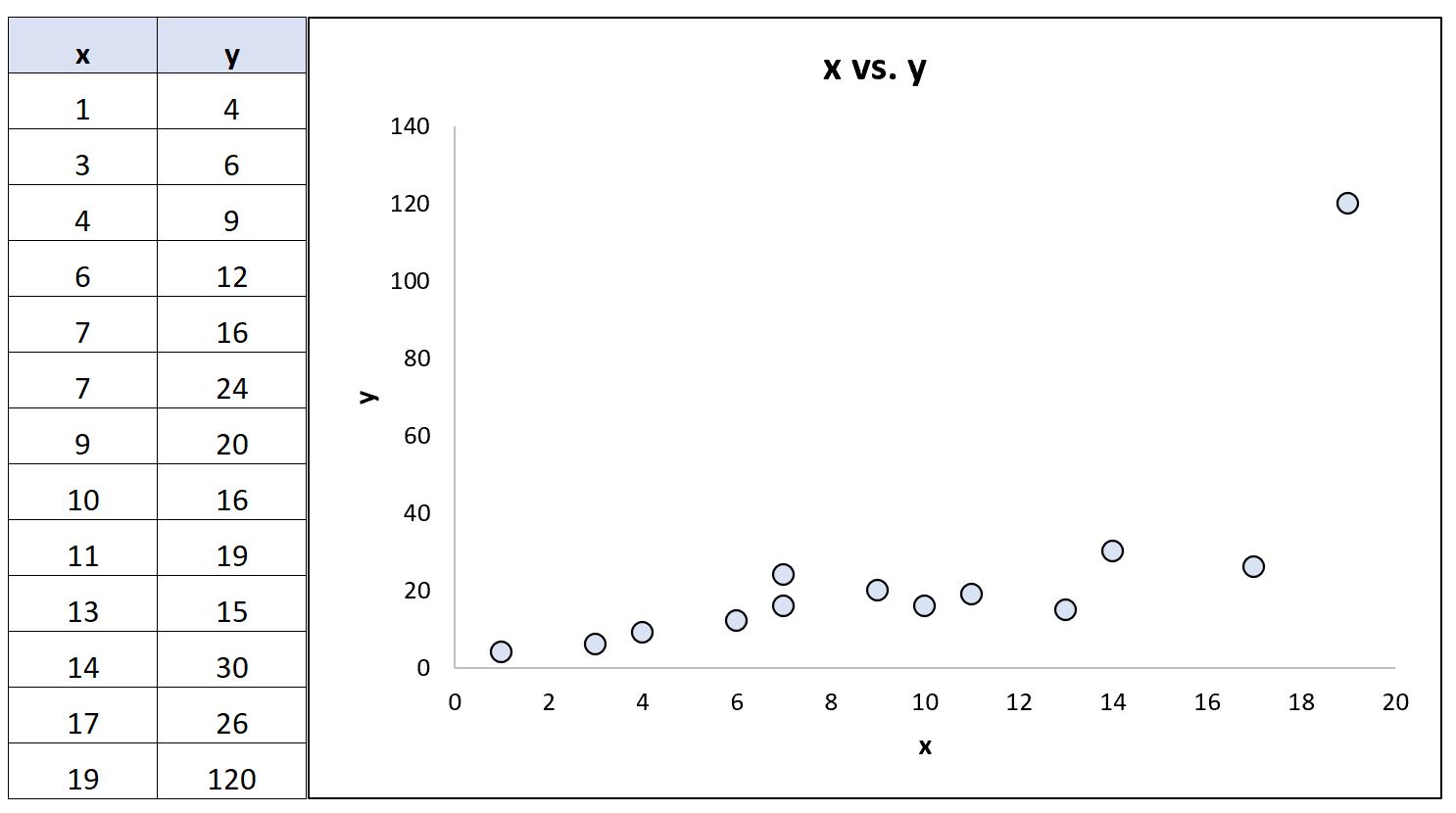
Korzystając z programów statystycznych, możemy przeliczyć współczynniki korelacji:

• Korelacja Pearsona: 0,69
• Korelacja rangi Spearmana: 0,85

Współczynnik korelacji Pearsona zmienił się istotnie, podczas gdy współczynnik korelacji rang Spearmana pozostał taki sam.

Używając żargonu statystycznego, powiedzielibyśmy, że związek między x i y jest monotoniczny (wraz ze wzrostem x, ogólnie wzrasta y), ale nie liniowy, ponieważ wartość odstająca ma duży wpływ na dane.

W tym scenariuszu korelacja rang Spearmana dobrze określa ilościowo tę monotoniczną zależność, podczas gdy korelacja Pearsona radzi sobie słabo, ponieważ próbuje obliczyć liniową zależność między dwiema zmiennymi.

Powiązane: Jak zgłosić korelację rangi Spearmana w formacie APA

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak obliczyć korelację rang Spearmana przy użyciu innego oprogramowania:

Jak obliczyć korelację rangi Spearmana w programie Excel
Jak obliczyć korelację rangi Spearmana w Arkuszach Google
Jak obliczyć korelację rang Spearmana w R
Jak obliczyć korelację rangi Spearmana w Pythonie