Kiedy warto zastosować wykres pudełkowy? (3 scenariusze)

Wykres pudełkowy to rodzaj wykresu przedstawiający pięciocyfrowe podsumowanie zbioru danych, które obejmuje:

• Wartość minimalna
• Pierwszy kwartyl (25. percentyl)
• Wartość średnia
• Trzeci kwartyl (75. percentyl)
• Maksymalna wartość

Aby utworzyć wykres pudełkowy dla dowolnego zbioru danych, wykonujemy trzy proste kroki:

• 1. Narysuj prostokąt od pierwszego do trzeciego kwartyla
• 2. Narysuj pionową linię na środku
• 3. Narysuj „wąsy” kwartylów do wartości minimalnej i maksymalnej

Zwykle tworzymy wykresy skrzynkowe w jednym z trzech scenariuszy:

Scenariusz 1: Wizualizuj rozkład wartości w zbiorze danych.

Wykres pudełkowy pozwala nam szybko zwizualizować rozkład wartości w zbiorze danych i zobaczyć, gdzie znajduje się pięć liczbowych wartości podsumowujących.

Scenariusz 2: porównanie dwóch lub więcej rozkładów.

Wykresy pudełkowe side-by-side pozwalają nam zwizualizować różnice pomiędzy dwoma lub większą liczbą rozkładów oraz porównać wartości mediany i rozkłady wartości pomiędzy rozkładami.

Scenariusz 3: Identyfikacja wartości odstających.

Na wykresach pudełkowych wartości odstające są zwykle reprezentowane przez małe okręgi wystające poza każdy wąs. Obserwację definiuje się jako odstającą, jeżeli spełnia jedno z poniższych kryteriów:

• Obserwacja jest mniejsza niż Q1 – 1,5*(Rozstęp międzykwartylowy)
• Obserwacja jest większa niż Q3 + 1,5*(Rozstęp międzykwartylowy)

Tworząc wykres pudełkowy, możemy szybko sprawdzić, czy rozkład ma wartości odstające.

Poniższe przykłady pokazują, jak użylibyśmy wykresu pudełkowego w każdym scenariuszu.

Scenariusz 1: Wizualizuj rozkład wartości w zbiorze danych

Załóżmy, że trener koszykówki chce zwizualizować rozkład punktów zdobytych przez zawodników swojej drużyny i dlatego tworzy następujący wykres pudełkowy:

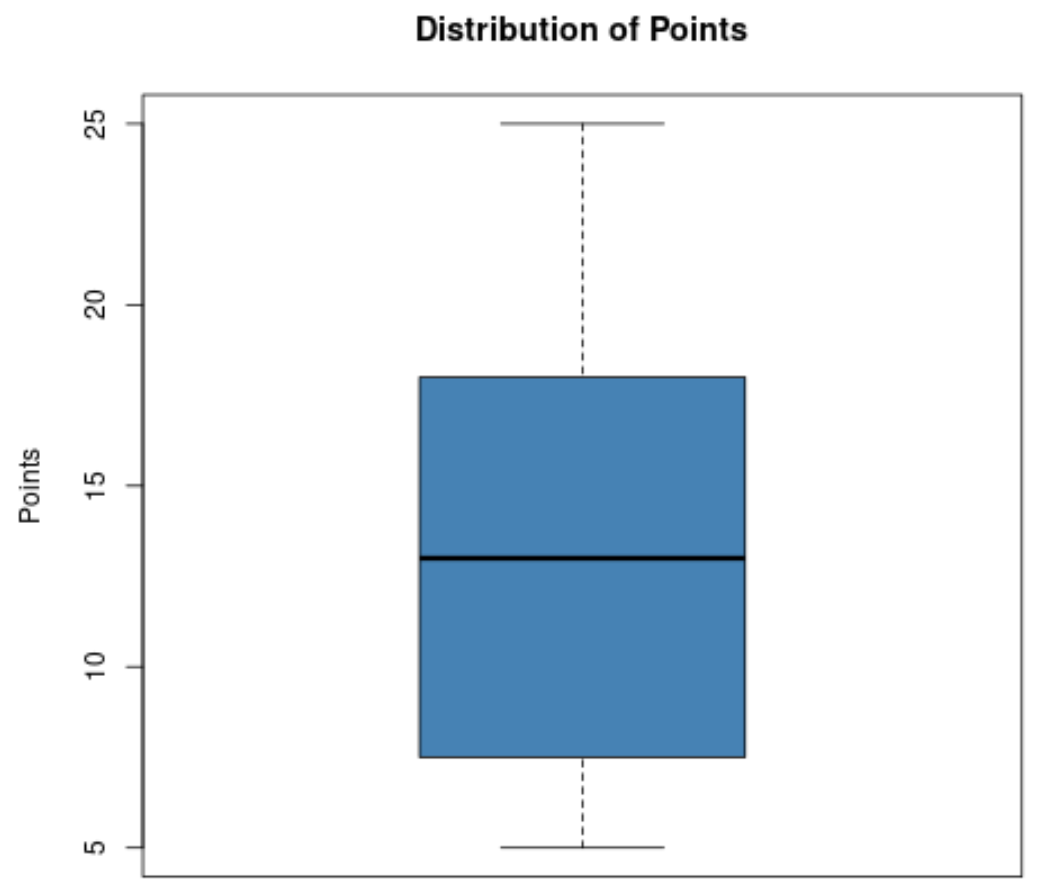
Na podstawie tego wykresu pudełkowego może szybko zobaczyć następujące wartości:

• Minimalna: 5
• T1 (pierwszy kwartyl): około 8
• Mediana: około 13
• T3 (trzeci kwartyl): około 18
• Maksymalnie: 25

Dzięki temu trener może szybko zorientować się, że punkty zdobyte przez zawodników wahają się od 5 do 25, że mediana zdobytych punktów wynosi około 13, a 50% jego zawodników zdobywa od około 8 do 18 punktów na mecz.

Scenariusz 2: Porównaj dwie lub więcej dystrybucji

Załóżmy, że analityk sportowy chce porównać rozkład punktów zdobytych przez koszykarzy w trzech różnych drużynach i tworzy następujące wykresy pudełkowe:

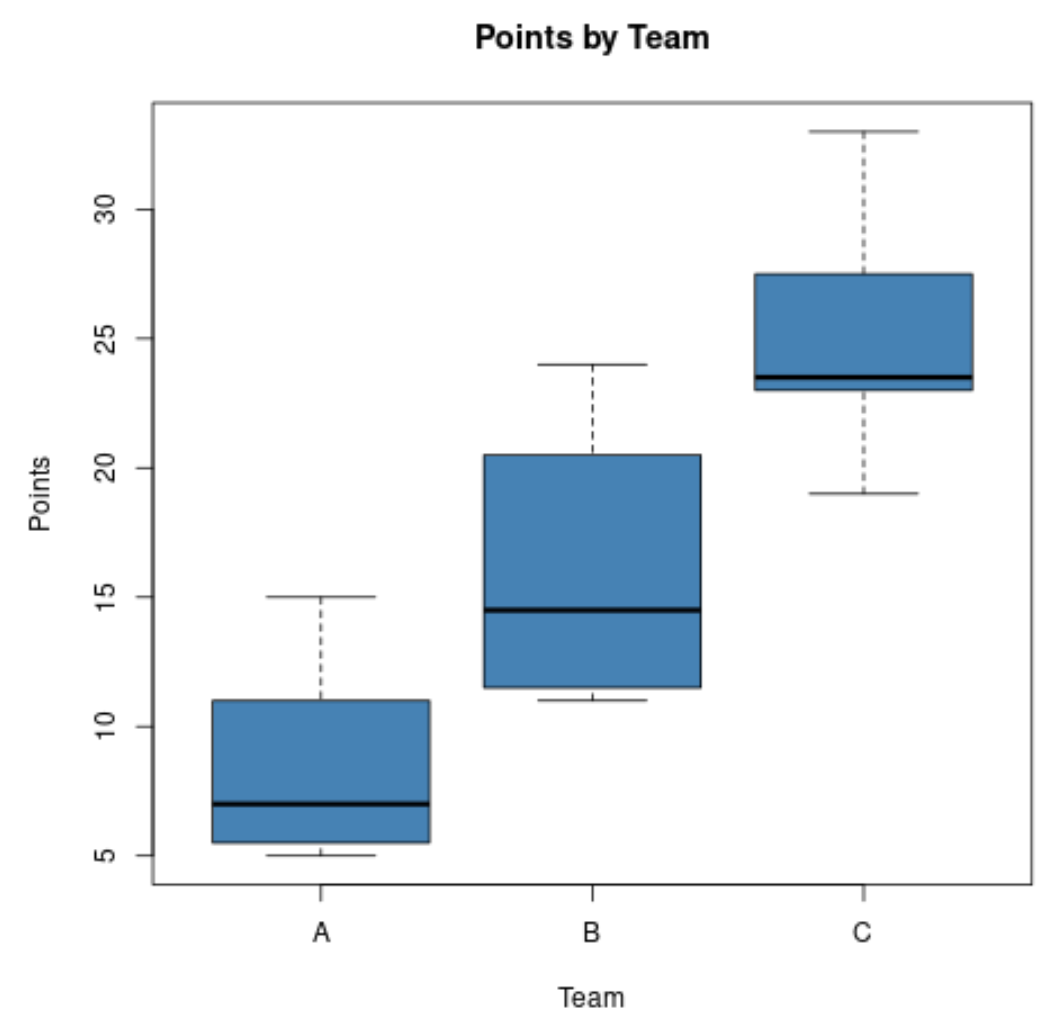
Korzystając z tych wykresów, może szybko sprawdzić, że drużyna C ma najwięcej zdobytych punktów środkowych, a drużyna A ma najmniej zdobytych punktów środkowych.

Może także szybko zauważyć, że Drużyna B ma największy rozkład zdobytych punktów, ponieważ wykres pudełkowy Drużyny B ma najdłuższe pudełko.

Scenariusz 3: Zidentyfikuj wartości odstające

Załóżmy, że trener koszykówki chce wiedzieć, czy jeden z jego zawodników wyróżnia się pod względem zdobytych punktów. Postanawia stworzyć następujący wykres pudełkowy, aby zwizualizować rozkład punktów zdobytych przez jego zawodników:

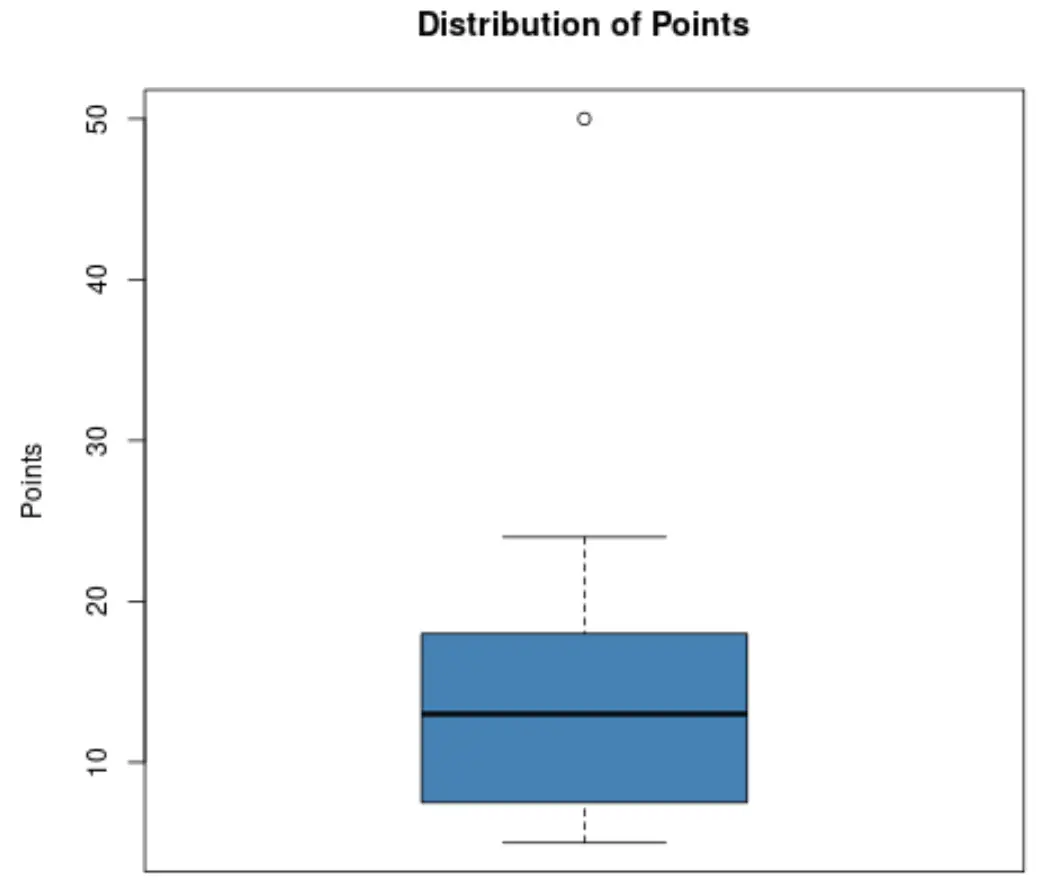
Korzystając z tego wykresu, trener może zobaczyć, że mała kropka na górze wykresu wskazuje wartość odstającą.

W szczególności jeden z graczy zdobył około 50 punktów, co jest uważane za wartość odstającą w porównaniu do wszystkich innych zdobytych punktów.

Dodatkowe zasoby

Poniższe samouczki zawierają szczegółowe wyjaśnienia dotyczące praktycznego wykorzystania wykresów skrzynkowych:

Jak znaleźć rozstęp międzykwartylowy (IQR) wykresu pudełkowego
Jak rozpoznać asymetrię na wykresach pudełkowych
Jak porównać wykresy pudełkowe

Poniższe samouczki wyjaśniają, jak tworzyć wykresy pudełkowe w różnych programach statystycznych:

Jak utworzyć wykres pudełkowy w Arkuszach Google
Jak tworzyć wykresy pudełkowe w SPSS
Jak tworzyć wykresy pudełkowe obok siebie w programie Excel
Jak utworzyć wykresy pudełkowe obok siebie w R