Jak wykonać test scheffe’a w r

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej niezależnych grup.

Jeśli ogólna wartość p tabeli ANOVA jest poniżej pewnego poziomu istotności, wówczas mamy wystarczające dowody, aby stwierdzić, że co najmniej jedna ze średnich grupowych różni się od pozostałych.

Nie mówi nam to jednak , które grupy różnią się od siebie. To po prostu mówi nam, że nie wszystkie średnie grupowe są równe.

Aby dokładnie wiedzieć, które grupy się od siebie różnią, musimy przeprowadzićtest post-hoc , który może kontrolować poziom błędów w przeliczeniu na rodzinę .

Jednym z najczęściej stosowanych testów post hoc jest test Scheffe’a.

W tym samouczku wyjaśniono, jak wykonać test Scheffe w języku R.

Przykład: test Scheffe’a w R

Załóżmy, że nauczyciel chce wiedzieć, czy trzy różne techniki uczenia się prowadzą do różnych wyników uczniów w testach. Aby to sprawdzić, losowo przydziela 10 uczniów do stosowania każdej techniki uczenia się i rejestruje wyniki ich egzaminów.

Możemy wykonać następujące kroki w języku R, aby dopasować jednokierunkową analizę ANOVA w celu sprawdzenia różnic w średnich wynikach egzaminów pomiędzy trzema grupami i użyć testu Scheffe’a, aby dokładnie określić, które grupy się różnią.

Krok 1: Utwórz zbiór danych.

Poniższy kod pokazuje, jak utworzyć zbiór danych zawierający wyniki egzaminów wszystkich 30 uczniów:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Krok 2: Wyświetl wyniki egzaminu dla każdej grupy.

Poniższy kod pokazuje, jak utworzyć wykresy skrzynkowe w celu wizualizacji rozkładu wyników egzaminu dla każdej grupy:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

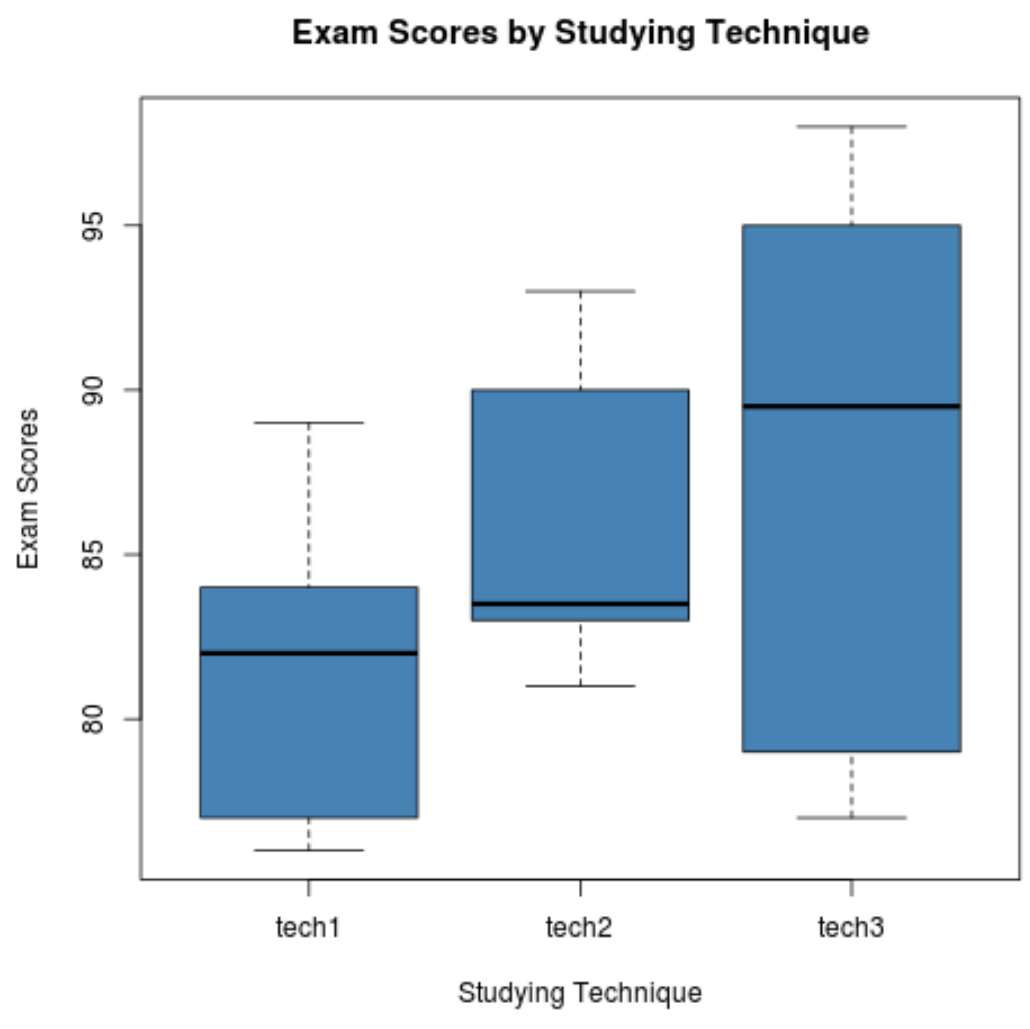
Krok 3: Wykonaj jednokierunkową ANOVA.

Poniższy kod pokazuje, jak przeprowadzić jednoczynnikową analizę ANOVA, aby sprawdzić różnice między średnimi wynikami egzaminu w każdej grupie:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ponieważ ogólna wartość p ( 0,0476 ) jest mniejsza niż 0,05, oznacza to, że każda grupa nie ma tego samego średniego wyniku z egzaminu.

Następnie przeprowadzimy test Scheffe’a, aby określić, które grupy są różne.

Krok 4: Wykonaj test Scheffe’a.

Do wykonania testu Scheffe’a użyjemy funkcji ScheffeTest() z pakietu DescTools .

Poniższy kod pokazuje, jak używać tej funkcji w naszym przykładzie:

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Sposób interpretacji wyniku jest następujący:

• Średnia różnica w wynikach egzaminu pomiędzy techniką 2 i techniką 1 wynosi 4,2 . Odpowiednia wartość p dla średniej różnicy wynosi 0,2582 .
• Średnia różnica w wynikach egzaminu pomiędzy techniką 3 i techniką 1 wynosi 6,4 . Odpowiednia wartość p dla średniej różnicy wynosi 0,0519 .
• Średnia różnica w wynikach egzaminu pomiędzy techniką 3 i techniką 2 wynosi 2,2 . Odpowiednia wartość p dla średniej różnicy wynosi 0,6803 .

W zależności od tego, jaki poziom istotności zdecydujemy się zastosować, jedyne dwie grupy, które wydają się statystycznie istotnie różne, to Technika 3 i Technika 1.

Dodatkowe zasoby

Jak wykonać jednokierunkową ANOVA w R
Jak wykonać test Tukeya w R
Jak wykonać poprawkę Bonferroniego w R