Jak wykonać poprawkę bonferroniego w r

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica między średnimi z trzech lub więcej niezależnych grup.

Jeśli ogólna wartość p tabeli ANOVA jest poniżej pewnego poziomu istotności, wówczas mamy wystarczające dowody, aby stwierdzić, że co najmniej jedna ze średnich grupowych różni się od pozostałych.

Nie mówi nam to jednak , które grupy różnią się od siebie. To po prostu mówi nam, że nie wszystkie średnie grupowe są równe.

Aby dokładnie wiedzieć, które grupy różnią się od siebie, musimy wykonać testy t parami pomiędzy każdą grupą, kontrolując współczynnik błędu rodzinnego .

Jednym z najczęstszych sposobów osiągnięcia tego jest użycie poprawki Bonferroniego przy obliczaniu wartości p dla każdego z par testów t.

W tym samouczku wyjaśniono, jak wykonać korektę Bonferroniego w języku R.

Przykład: korekta Bonferroniego w R

Załóżmy, że nauczyciel chce wiedzieć, czy trzy różne techniki uczenia się prowadzą do różnych wyników uczniów w testach.

Aby to sprawdzić, losowo przydziela 10 uczniów do stosowania każdej techniki uczenia się. Po tygodniu stosowania przypisanej mu techniki nauki każdy uczeń przystępuje do tego samego egzaminu.

Możemy wykonać następujące kroki w R, aby dopasować jednokierunkową ANOVA i użyć poprawki Bonferroniego do obliczenia różnic parami między wynikami egzaminu każdej grupy.

Krok 1: Utwórz zbiór danych.

Poniższy kod pokazuje, jak utworzyć zbiór danych zawierający wyniki egzaminów wszystkich 30 uczniów:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Krok 2: Wyświetl wyniki egzaminu dla każdej grupy.

Poniższy kod pokazuje, jak utworzyć wykresy skrzynkowe w celu wizualizacji rozkładu wyników egzaminu dla każdej grupy:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

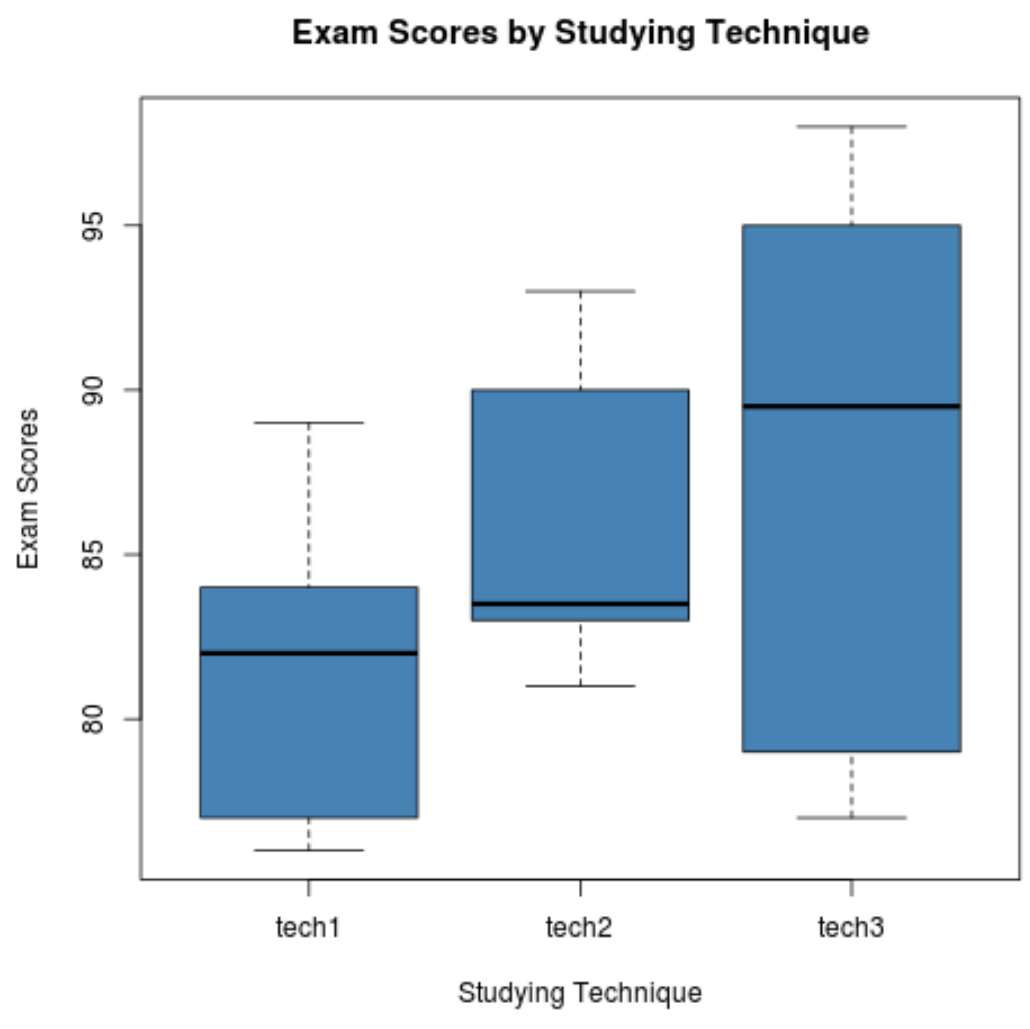
Krok 3: Wykonaj jednokierunkową ANOVA.

Poniższy kod pokazuje, jak przeprowadzić jednoczynnikową analizę ANOVA, aby sprawdzić różnice między średnimi wynikami egzaminu w każdej grupie:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Ponieważ ogólna wartość p ( 0,0476 ) jest mniejsza niż 0,05, oznacza to, że każda grupa nie ma tego samego średniego wyniku z egzaminu.

Następnie przeprowadzimy testy t dla par, korzystając z poprawki Bonferroniego dla wartości p, aby obliczyć różnice parami między wynikami egzaminu każdej grupy.

Krok 4: Wykonaj testy t parami.

Aby wykonać testy t parami z poprawką Bonferroniego w R, możemy użyć funkcji pairwise.t.test() , która wykorzystuje następującą składnię:

pairwise.t.test(x, g, p.just.method=”bonferroni”)

Złoto:

• x: wektor liczbowy wartości odpowiedzi
• g: wektor określający nazwy grup (np. technika badania)

Poniższy kod pokazuje, jak używać tej funkcji w naszym przykładzie:

 #perform pairwise t-tests with Bonferroni's correction
pairwise.t.test(data$score, data$technique, p.adjust.method=" bonferroni ")

	Pairwise comparisons using t tests with pooled SD 

data: data$score and data$technique 

      tech1 tech2
tech2 0.309 -    
tech3 0.048 1.000

P value adjustment method: bonferroni

Sposób interpretacji wyniku jest następujący:

• Skorygowana wartość p dla średniej różnicy w wynikach egzaminu pomiędzy Techniką 1 i Techniką 2 wynosi 0,309 .
• Skorygowana wartość p dla średniej różnicy w wynikach egzaminu pomiędzy Techniką 1 i Techniką 3 wynosi 0,048 .
• Skorygowana wartość p dla średniej różnicy w wynikach egzaminu pomiędzy Techniką 2 i Techniką 3 wynosi 1000 .

Na podstawie wyników widzimy, że jedyna znacząca różnica występuje pomiędzy techniką 1 i techniką 3.

Dodatkowe zasoby

Wprowadzenie do jednokierunkowej ANOVA
Jak wykonać jednokierunkową ANOVA w R
Jak wykonać test Tukeya w R
Jak wykonać test Dunnetta w R