Proste wyjaśnienie korekty ciągłości w statystyce
Korekcja ciągłości jest stosowana, gdy chcesz użyć rozkładu ciągłego w celu przybliżenia rozkładu dyskretnego. Zwykle używa się go, gdy rozkład normalny ma być przybliżony do rozkładu dwumianowego .
Przypomnijmy, że rozkład dwumianowy mówi nam o prawdopodobieństwie osiągnięcia x sukcesu w n próbach, zakładając, że prawdopodobieństwo sukcesu w pojedynczej próbie wynosi p . Aby odpowiedzieć na pytania dotyczące prawdopodobieństwa za pomocą rozkładu dwumianowego, możemy po prostu użyć kalkulatora rozkładu dwumianowego , ale możemy również przybliżyć prawdopodobieństwo za pomocą rozkładu normalnego z poprawką na ciągłość.
Korekta ciągłości to nazwa nadana dodaniu lub odjęciu 0,5 od dyskretnej wartości x .
Załóżmy na przykład, że chcemy znaleźć prawdopodobieństwo, że moneta wyląduje na orle mniejszym lub równym 45 razy w ciągu 100 rzutów. Oznacza to, że chcemy znaleźć P(X ≤ 45). Aby użyć rozkładu normalnego do przybliżenia rozkładu dwumianowego, zamiast tego znaleźlibyśmy P(X ≤ 45,5).
Poniższa tabela pokazuje, kiedy należy dodać lub odjąć 0,5, w zależności od rodzaju prawdopodobieństwa, które próbujesz znaleźć:
| Skorzystaj z rozkładu dwumianowego | Stosowanie rozkładu normalnego z korektą na ciągłość |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X < 45,5 |
| X < 45 | X < 44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Notatka:
Właściwe jest zastosowanie poprawki na ciągłość rozkładu normalnego w celu przybliżenia rozkładu dwumianowego, gdy oba n*p i n*(1-p) wynoszą co najmniej 5.
Załóżmy na przykład, że n = 15 i p = 0,6. W tym przypadku:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Ponieważ obie te liczby są większe lub równe 5, w tym scenariuszu dopuszczalne byłoby zastosowanie korekty ciągłości.
Poniższy przykład ilustruje, jak zastosować korekcję ciągłości do rozkładu normalnego w celu przybliżenia rozkładu dwumianowego.
Przykład zastosowania korekcji ciągłości
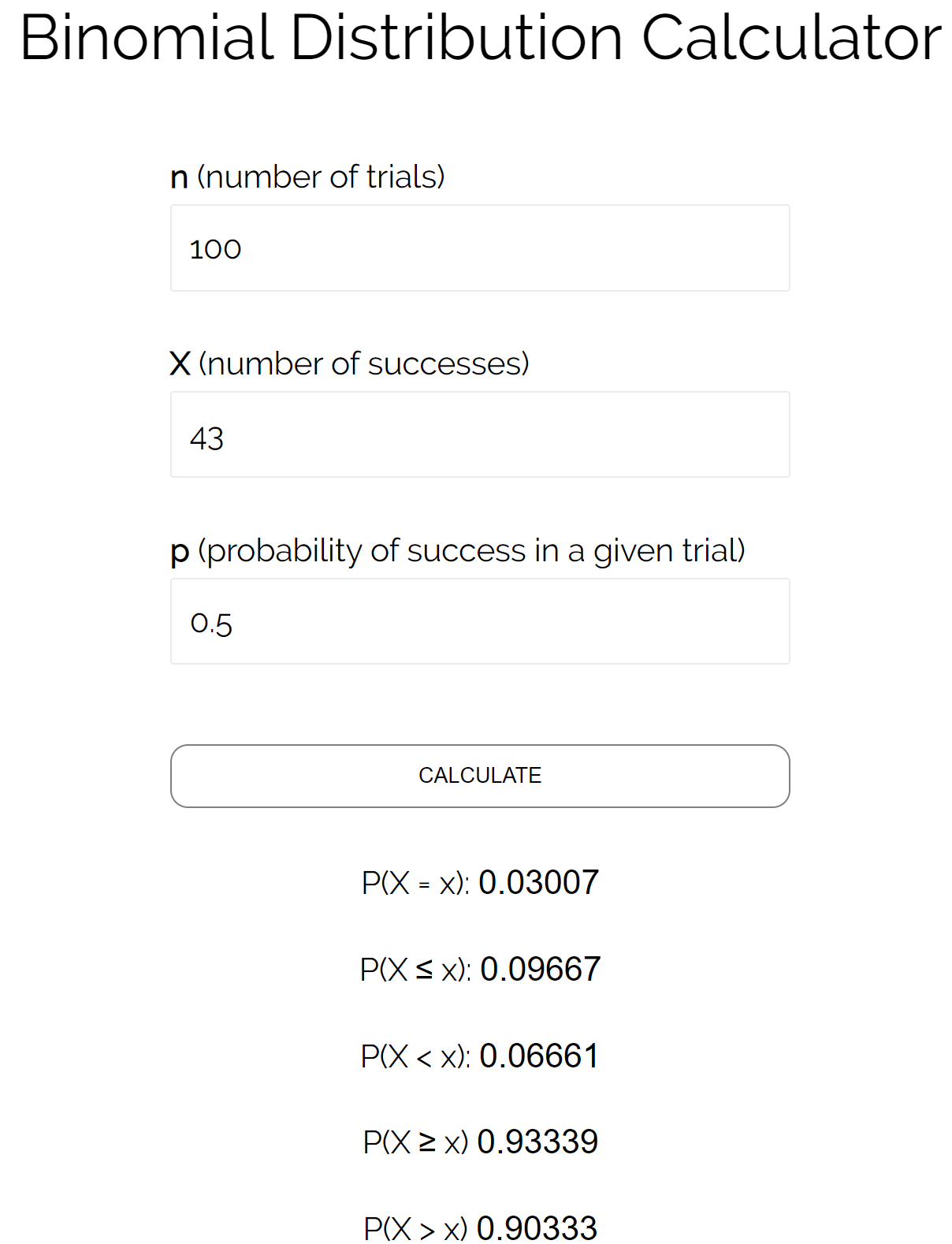
Załóżmy, że chcemy poznać prawdopodobieństwo, że moneta wyląduje na orle mniejszym lub równym 43 razy w 100 rzutach. W tym przypadku:
n = liczba prób = 100
X = liczba sukcesów = 43
p = prawdopodobieństwo sukcesu w danej próbie = 0,50
Możemy podłączyć te liczby do kalkulatora rozkładu dwumianowego i zobaczyć, że prawdopodobieństwo wyrzucenia reszki mniejszego lub równego 43 razy wynosi 0,09667 .
Aby przybliżyć rozkład dwumianowy poprzez zastosowanie poprawki na ciągłość rozkładu normalnego, możemy wykonać następujące kroki:
Krok 1: Sprawdź, czy oba n*p i n*(1-p) wynoszą co najmniej 5 .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Obie liczby są większe lub równe 5, więc możemy kontynuować.
Krok 2: Ustal, czy dodać, czy odjąć 0,5
Odnosząc się do powyższej tabeli widzimy, że gdy pracujemy z prawdopodobieństwem w postaci X ≤ 43, powinniśmy dodać 0,5. W ten sposób znajdziemy P(X< 43,5).
Krok 3: Znajdź średnią (μ) i odchylenie standardowe (σ) rozkładu dwumianowego.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*,5*(1-,5) = √ 25 = 5
Krok 4: Znajdź wynik z, korzystając ze średniej i odchylenia standardowego znalezionych w poprzednim kroku.
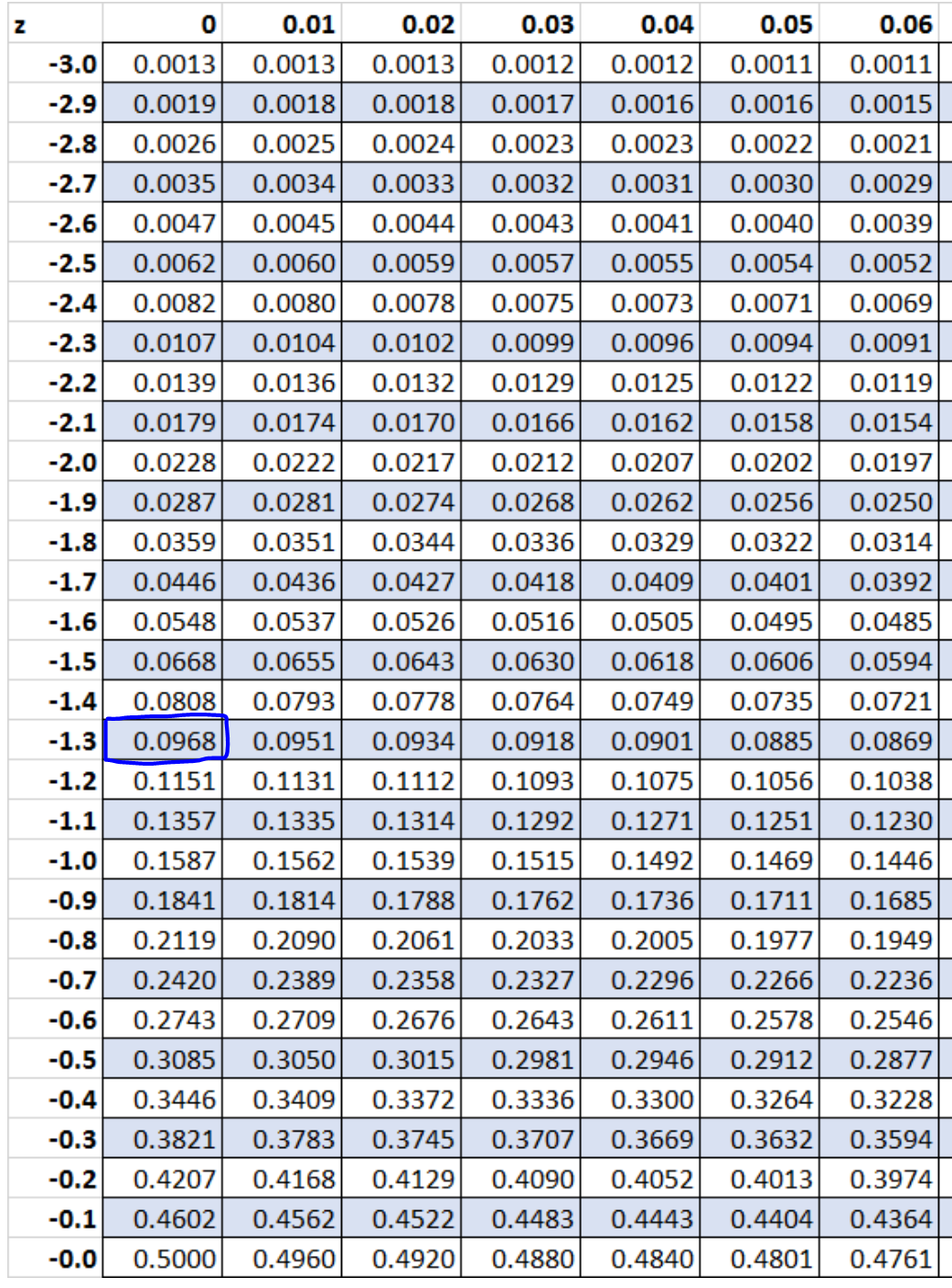
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
Krok 5: Skorzystaj z tabeli Z, aby znaleźć prawdopodobieństwo powiązane z wynikiem z.
Według tabeli Z prawdopodobieństwo związane z z = -1,3 wynosi 0,0968 .
Zatem dokładne prawdopodobieństwo, które obliczyliśmy na podstawie rozkładu dwumianowego, wyniosło 0,09667 , podczas gdy przybliżone prawdopodobieństwo, które obliczyliśmy na podstawie poprawki na ciągłość z rozkładem normalnym, wyniosło 0,0968 . Te dwie wartości są dość zamknięte.
Kiedy stosować korekcję ciągłości
Zanim istniało nowoczesne oprogramowanie statystyczne i obliczenia musiały być wykonywane ręcznie, często stosowano poprawki na ciągłość w celu znalezienia prawdopodobieństw obejmujących rozkłady dyskretne. Obecnie poprawki na ciągłość odgrywają mniejszą rolę w obliczaniu prawdopodobieństw, ponieważ zwykle możemy polegać na oprogramowaniu lub kalkulatorach, aby obliczyć prawdopodobieństwa.
Zamiast tego jest to po prostu temat poruszany na kursach statystyki, mający na celu zilustrowanie związku między rozkładem dwumianowym a rozkładem normalnym oraz pokazanie, że rozkład normalny może aproksymować rozkład dwumianowy poprzez zastosowanie poprawki na ciągłość.
Kalkulator korekcji ciągłości
Użyj kalkulatora korekcji ciągłości , aby automatycznie zastosować korekcję ciągłości do rozkładu normalnego w celu przybliżenia prawdopodobieństw dwumianowych.