Korekta ciągłości yate: definicja i przykład

Test niezależności chi-kwadrat służy do określenia, czy istnieje istotny związek między dwiema zmiennymi kategorycznymi.

W teście tym wykorzystuje się następujące hipotezy zerowe i alternatywne:

• H ₀ : (hipoteza zerowa) Te dwie zmienne są niezależne.
• H ₁ : (hipoteza alternatywna) Te dwie zmienne nie są niezależne. (tj. są powiązane)

Do obliczenia statystyki testu Chi-kwadrat x ² dla tego testu używamy następującego wzoru:

X ² = Σ(O _i -E _ja ) ² / E _ja

Złoto:

• Σ: to fantazyjny symbol oznaczający „sumę”
• O: obserwowana wartość
• E: wartość oczekiwana

W tym teście założono, że dyskretne prawdopodobieństwa częstotliwości w tabeli kontyngencji można aproksymować za pomocą rozkładu Chi-kwadrat, który jest rozkładem ciągłym.

Jednak to założenie jest zwykle nieco błędne, a uzyskane statystyki testowe są zwykle zawyżane.

Aby skorygować to odchylenie, możemy zastosować korektę ciągłości Yate’a , która stosuje następującą poprawkę do wzoru ^X2 :

X ² = Σ(|O _i -E _i | – 0,5) ² / E _ja

Zwykle używamy tej poprawki tylko wtedy, gdy co najmniej jedna komórka w tabeli kontyngencji ma oczekiwaną częstotliwość mniejszą niż 5.

Przykład: zastosowanie poprawki na ciągłość Yate’a

Załóżmy, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy prostą losową próbę 40 wyborców i pytamy ich o preferencje dotyczące partii politycznych. Wyniki badania prezentuje poniższa tabela:

Oto jak wykonać test niezależności chi-kwadrat z korektą ciągłości Yate’a:

Obserwowane wartości:

Oczekiwane wartości:

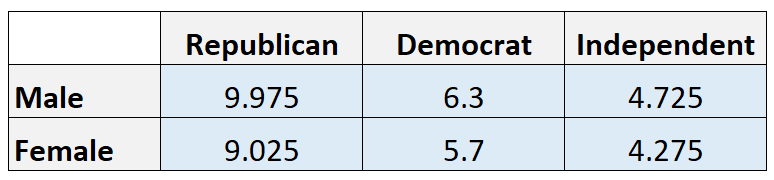
Uwaga: wartość oczekiwaną obliczamy w każdej komórce, mnożąc sumę wiersza przez sumę kolumny, a następnie dzieląc przez sumę całkowitą. Na przykład oczekiwana liczba mężczyzn z Partii Republikańskiej wynosi (21*19)/40 = 9,975.

_{Statystyka testu} ^{chi –} _kwadrat :

• (|8-9,975| – 0,5) ² / 9,975 = 0,218
• (|9-6,3| – 0,5) ² / 6,3 = 0,768
• (|4-4,725| – 0,5) ² / 4,725 = 0,011
• (|11-9,025| – 0,5) ² / 9,025 = 0,241
• (|3-5,7| – 0,5) ² / 5,7 = 0,849
• (|5-4,275| – 0,5) ² / 4,275 = 0,012

^Więc ,

Wartość P: Według kalkulatora wartości chi-kwadrat na wartość P , wartość p odpowiadająca statystyce testowej chi-kwadrat z 2 stopniami swobody wynosi 0,3501 .

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie uda nam się odrzucić hipotezy zerowej. Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że istnieje związek między płcią a preferencjami partii politycznych.