Jak obliczyć korelację krzyżową w r

Korelacja krzyżowa to sposób pomiaru stopnia podobieństwa między szeregiem czasowym a opóźnioną wersją innego szeregu czasowego.

Ten typ korelacji jest przydatny do obliczeń, ponieważ może nam powiedzieć, czy wartości w jednym szeregu czasowym przewidują przyszłe wartości w innym szeregu czasowym. Innymi słowy, może nam powiedzieć, czy jeden szereg czasowy jest wiodącym wskaźnikiem dla innego szeregu czasowego.

Ten typ korelacji jest stosowany w wielu różnych dziedzinach, w tym:

Gospodarka: Wskaźnik zaufania konsumentów (CCI) jest uważany za wiodący wskaźnik produktu krajowego brutto (PKB) danego kraju. Na przykład, jeśli CCI jest wysoki w danym miesiącu, PKB prawdopodobnie będzie wyższy x miesięcy później.

Firmy: Wydatki na marketing są często uważane za wiodący wskaźnik przyszłych przychodów firmy. Na przykład, jeśli firma wydaje niezwykle dużą kwotę na marketing w jednym kwartale, wówczas całkowite przychody powinny być wysokie x kwartałów później.

Biologia: Całkowite zanieczyszczenie oceanów jest uważane za wiodący wskaźnik populacji określonego gatunku żółwia. Na przykład, jeśli w danym roku zanieczyszczenie jest wyższe, oczekuje się, że całkowita populacja żółwi zmniejszy się x lat później.

Poniższy przykład pokazuje, jak obliczyć korelację krzyżową między dwoma szeregami czasowymi w R.

Przykład: Jak obliczyć korelację krzyżową w R

Załóżmy, że mamy w R następujący szereg czasowy, który pokazuje całkowite wydatki marketingowe (w tysiącach) określonej firmy, a także całkowity przychód (w tysiącach) przez 12 kolejnych miesięcy:

 #define data
marketing <- c(3, 4, 5, 5, 7, 9, 13, 15, 12, 10, 8, 8)
revenue <- c(21, 19, 22, 24, 25, 29, 30, 34, 37, 40, 35, 30)

Korelację krzyżową dla każdego opóźnienia pomiędzy dwoma szeregami czasowymi możemy obliczyć za pomocą funkcji ccf() w następujący sposób:

 #calculate cross correlation
ccf(marketing, revenue)

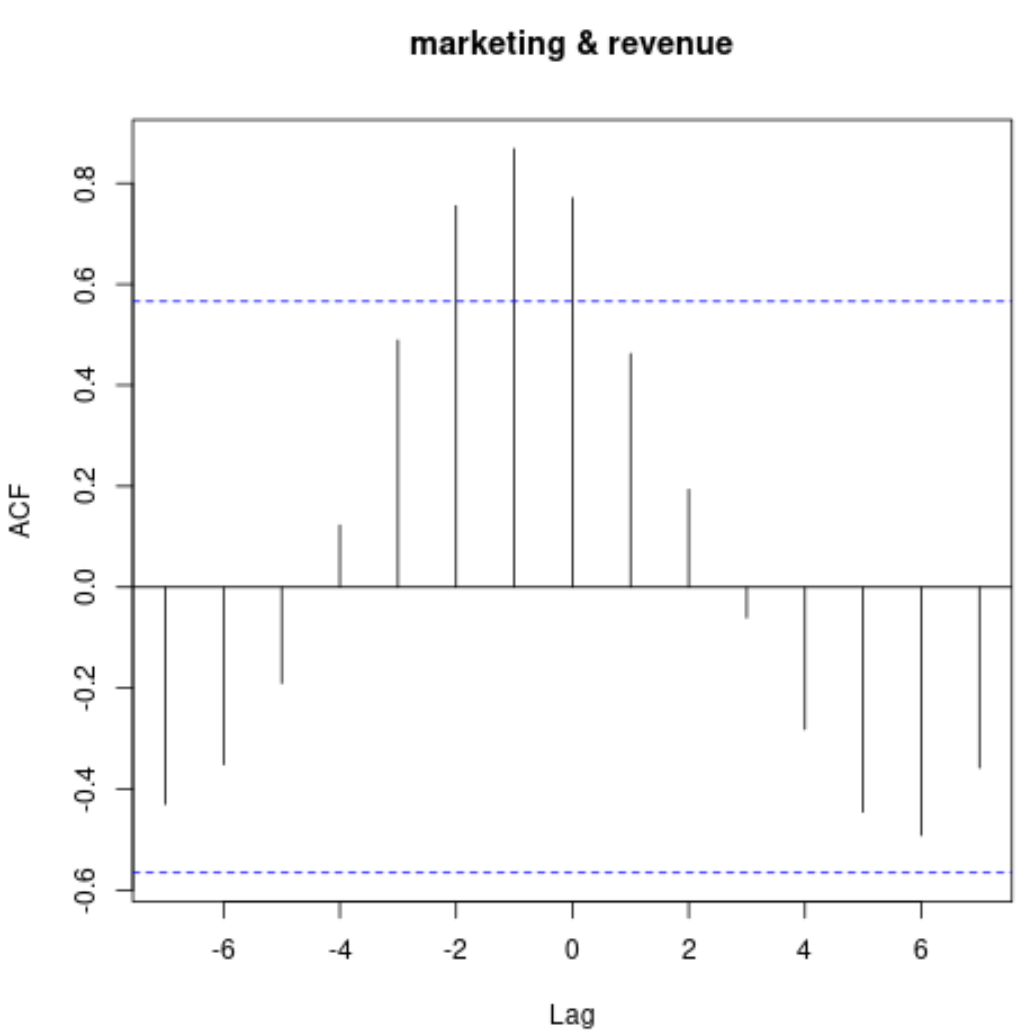
Ten wykres przedstawia korelację między dwoma szeregami czasowymi przy różnych opóźnieniach.

Aby wyświetlić rzeczywiste wartości korelacji, możemy zastosować następującą składnię:

 #display cross correlation values
print (ccf(marketing, revenue))

Autocorrelations of series 'X', by lag

    -7 -6 -5 -4 -3 -2 -1 0 1 2 3 
-0.430 -0.351 -0.190 0.123 0.489 0.755 0.868 0.771 0.462 0.194 -0.061 
     4 5 6 7 
-0.282 -0.445 -0.492 -0.358

Oto jak zinterpretować ten wynik:

• Korelacja krzyżowa przy opóźnieniu 0 wynosi 0,771 .
• Korelacja krzyżowa przy opóźnieniu 1 wynosi 0,462 .
• Korelacja krzyżowa przy opóźnieniu 2 wynosi 0,194 .
• Korelacja krzyżowa przy opóźnieniu 3 wynosi -0,061 .

I tak dalej.

Należy zauważyć, że korelacja między tymi dwoma szeregami czasowymi jest dość dodatnia z opóźnieniami od -2 do 2, co mówi nam, że wydatki marketingowe w danym miesiącu dość dobrze przewidują przychody miesiąc i dwa później.

Ma to intuicyjny sens: spodziewamy się, że wysokie wydatki marketingowe w danym miesiącu będą przewidywać wzrost przychodów w ciągu najbliższych dwóch miesięcy.

Dodatkowe zasoby

Jak obliczyć autokorelację w R
Jak obliczyć korelację częściową w R
Jak obliczyć korelację przesuwną w R