Jak obliczyć korelację między zmiennymi ciągłymi i kategorialnymi

Kiedy chcemy obliczyć korelację między dwiema zmiennymi ciągłymi, zazwyczaj używamy współczynnika korelacji Pearsona .

Jeśli jednak chcemy obliczyć korelację między zmienną ciągłą a zmienną kategoryczną , możemy zastosować tak zwaną korelację punktową dwuseryjną .

Korelacja dwuseryjna punktowa służy do obliczania korelacji pomiędzy binarną zmienną kategorialną (zmienną, która może przyjmować tylko dwie wartości) a zmienną ciągłą i ma następujące właściwości:

• Korelacja punktowo-biserialna może zmieniać się w zakresie od -1 do 1.
• Dla każdej grupy utworzonej przez zmienną binarną zakłada się, że zmienna ciągła ma rozkład normalny z równymi wariancjami.
• Dla każdej grupy utworzonej przez zmienną binarną zakłada się, że nie ma skrajnych wartości odstających.

Poniższy przykład pokazuje, jak w praktyce obliczyć korelację punktowo-dwerialną.

Przykład: Obliczenie korelacji punktowo-dwseryjnej

Załóżmy, że profesor uniwersytetu chce ustalić, czy istnieje korelacja między płcią a wynikiem na konkretnym egzaminie kwalifikacyjnym.

Zbiera następujące dane na temat 12 chłopców i 12 dziewcząt w swojej klasie:

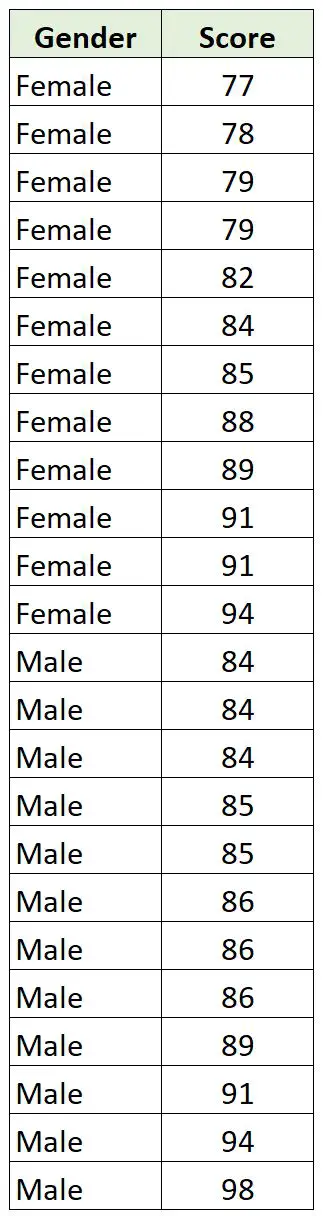
Ponieważ płeć jest zmienną kategoryczną, a wynik jest zmienną ciągłą, sensowne jest obliczenie korelacji punktowo-dwuseryjnej między tymi dwiema zmiennymi.

Profesor potrafi wykorzystać dowolny program statystyczny (m.in. Excel, R, Python, SPSS, Stata) do obliczenia korelacji punktowo-biseryjnej pomiędzy obiema zmiennymi.

Poniższy kod pokazuje, jak obliczyć korelację punktowo-dwseryjną w R, używając wartości 0 do reprezentowania kobiet i 1 do reprezentowania mężczyzn dla zmiennej płci:

 #define values for gender
gender <- c(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
            1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1)

#define values for score
score <- c(77, 78, 79, 79, 82, 84, 85, 88, 89, 91, 91, 94,
           84, 84, 84, 85, 85, 86, 86, 86, 89, 91, 94, 98)

#calculate point-biserial correlation
horn. test (gender, score)

	Pearson's product-moment correlation

data: gender and score
t = 1.3739, df = 22, p-value = 0.1833
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 -0.1379386 0.6147832
sample estimates:
      horn 
0.2810996

Z wyniku widzimy, że współczynnik korelacji punktowo-dwseryjnej wynosi 0,281 , a odpowiadająca mu wartość p wynosi 0,1833 .

Ponieważ współczynnik korelacji jest dodatni, oznacza to, że istnieje dodatnia korelacja między płcią a wynikiem.

Ponieważ zakodowaliśmy mężczyzn jako 1, a kobiety jako 0, oznacza to, że wyniki są zwykle wyższe w przypadku mężczyzn (tj. wyniki mają tendencję do zwiększania się wraz ze „wzrostem” płci). » od 0 do 1).

Ponieważ jednak wartość p jest nie mniejsza niż 0,05, ten współczynnik korelacji nie jest istotny statystycznie.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak obliczyć korelację punktową dwuseryjną przy użyciu różnych programów statystycznych:

Jak obliczyć korelację punktowo-dwerialną w programie Excel
Jak obliczyć korelację punktowo-biseryjną w R
Jak obliczyć korelację punktowo-biseryjną w Pythonie