Jak obliczyć korelację pomiędzy zmiennymi kategorycznymi

Często używamy współczynnika korelacji Pearsona do obliczenia korelacji pomiędzy ciągłymi zmiennymi numerycznymi.

Musimy jednak użyć innej metryki, aby obliczyć korelację między zmiennymi kategorycznymi, to znaczy zmiennymi, które przyjmują nazwy lub etykiety, takie jak:

• Stan cywilny (panny, żonaty, rozwiedziony)
• Status palenia (palący, niepalący)
• Kolor oczu (niebieski, brązowy, zielony)

Istnieją trzy powszechnie stosowane miary do obliczania korelacji między zmiennymi kategorycznymi:

1. Korelacja tetrachoryczna: stosowana do obliczania korelacji pomiędzy binarnymi zmiennymi kategorycznymi.

2. Korelacja polichoryczna: stosowana do obliczania korelacji pomiędzy porządkowymi zmiennymi kategorycznymi.

3. V Cramera: stosowany do obliczania korelacji pomiędzy nominalnymi zmiennymi kategorycznymi.

W poniższych sekcjach przedstawiono przykład obliczania każdego z tych trzech pomiarów.

Metryka 1: Korelacja tetrachoryczna

Korelacja tetrachoryczna służy do obliczania korelacji między binarnymi zmiennymi kategorycznymi. Pamiętaj, że zmienne binarne to zmienne, które mogą przyjmować tylko jedną z dwóch możliwych wartości.

Wartość korelacji tetrachorycznej mieści się w zakresie od -1 do 1, gdzie -1 oznacza silną korelację ujemną, 0 oznacza brak korelacji, a 1 oznacza silną korelację dodatnią.

Załóżmy na przykład, że chcemy wiedzieć, czy płeć jest powiązana z preferencją partii politycznej. Bierzemy więc prostą losową próbę 100 wyborców i pytamy ich o preferencje dotyczące partii politycznej.

Wyniki badania prezentuje poniższa tabela:

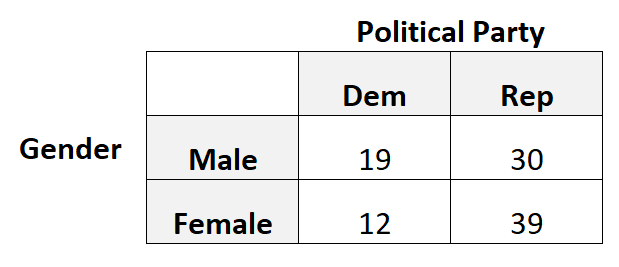
W tym scenariuszu użylibyśmy korelacji tetrachorycznej, ponieważ każda zmienna kategoryczna jest binarna, to znaczy każda zmienna może przyjmować tylko dwie możliwe wartości.

Możemy użyć następującego kodu w R, aby obliczyć korelację tetrachoryczną między dwiema zmiennymi:

 library (psych)

#create 2x2 table
data = matrix(c(19, 12, 30, 39), nrow= 2 )

#view table
data

#calculate tetrachoric correlation
tetrachoric(data)

tetrachoric correlation 
[1] 0.27

Okazuje się, że korelacja tetrachoryczna wynosi 0,27 . Wartość ta jest dość niska, co wskazuje, że istnieje słaby (jeśli w ogóle) związek między płcią a preferencjami partii politycznych.

Metryka 2: Korelacja polichoryczna

Korelacja polichoryczna służy do obliczania korelacji między porządkowymi zmiennymi kategorycznymi. Przypomnijmy, że zmienne porządkowe to zmienne, których możliwe wartości mają naturalny porządek.

Wartość korelacji polichorycznej waha się od -1 do 1, gdzie -1 oznacza silną korelację ujemną, 0 oznacza brak korelacji, a 1 oznacza silną korelację dodatnią.

Załóżmy na przykład, że chcesz wiedzieć, czy dwie różne agencje oceniające filmy mają wysoką korelację między ocenami filmów.

Prosimy każdą agencję o ocenę 20 różnych filmów w skali od 1 do 3, gdzie 1 oznacza „zły”, 2 oznacza „słaby”, a 3 oznacza „dobry”.

Poniższa tabela przedstawia wyniki:

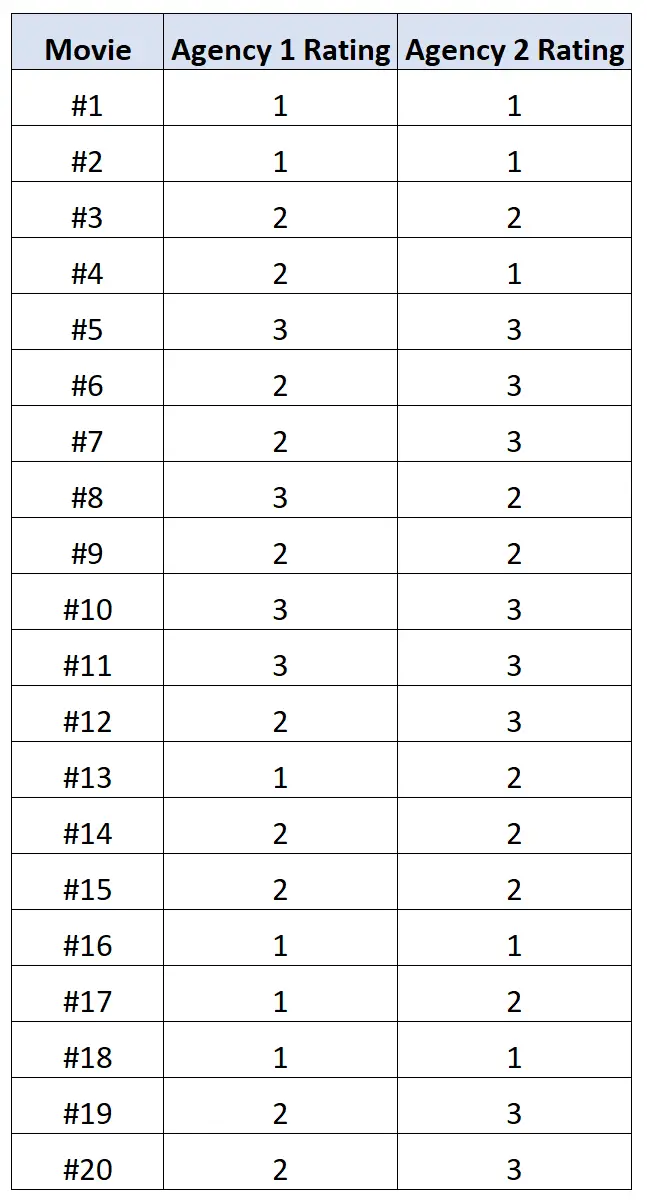
Możemy użyć następującego kodu w R, aby obliczyć polichoryczną korelację między ratingami dwóch agencji:

 library (polycor)

#define movie ratings
x <- c(1, 1, 2, 2, 3, 2, 2, 3, 2, 3, 3, 2, 1, 2, 2, 1, 1, 1, 2, 2)
y <- c(1, 1, 2, 1, 3, 3, 3, 2, 2, 3, 3, 3, 2, 2, 2, 1, 2, 1, 3, 3)

#calculate polychoric correlation between ratings
polychor(x, y)

[1] 0.7828328

Okazuje się, że korelacja polichoryczna wynosi 0,78 . Wartość ta jest dość wysoka, co wskazuje, że istnieje silny pozytywny związek pomiędzy ocenami poszczególnych agencji.

Metryka 3: V Cramera

Do obliczenia korelacji między nominalnymi zmiennymi kategorycznymi stosuje się współczynnik V Cramera . Pamiętaj, że zmienne nominalne to te, które mają etykiety kategorii, ale nie mają naturalnego porządku.

Wartość V Cramera waha się od 0 do 1, gdzie 0 oznacza brak związku między zmiennymi, a 1 wskazuje na silny związek między zmiennymi.

Załóżmy na przykład, że chcemy wiedzieć, czy istnieje korelacja między kolorem oczu a płcią. Przesłuchujemy zatem 50 osób i uzyskujemy następujące wyniki:

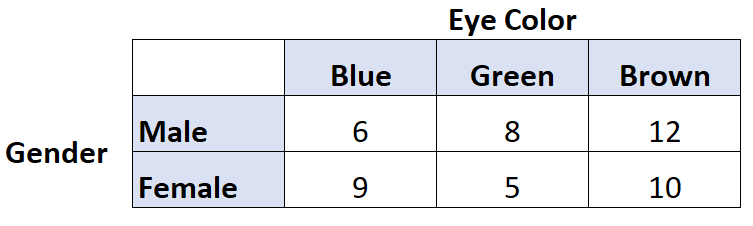
Możemy użyć następującego kodu w R, aby obliczyć V Cramera dla tych dwóch zmiennych:

 library (rcompanion)

#create table
data = matrix(c(6, 9, 8, 5, 12, 10), nrow= 2 )

#view table
data

     [,1] [,2] [,3]
[1,] 6 8 12
[2,] 9 5 10

#calculate Cramer's V
cramerV(data)

Cramer V 
  0.1671

Okazuje się, że V Cramera wynosi 0,1671 . Wartość ta jest dość niska, co wskazuje, że istnieje słaby związek między płcią a kolorem oczu.

Dodatkowe zasoby

Wprowadzenie do współczynnika korelacji Pearsona
Wprowadzenie do korelacji tetrachorycznej
Zmienne kategoryczne lub ilościowe: jaka jest różnica?
Poziomy pomiaru: nominalny, porządkowy, interwałowy i ilorazowy