Korelacja a regresja: jaka jest różnica?

Korelacja i regresja to dwa powiązane, ale nie całkowicie takie same terminy statystyczne.

W tym samouczku przedstawimy krótkie wyjaśnienie obu terminów i wyjaśnimy, w jaki sposób są one podobne i różne.

Co to jest korelacja?

Korelacja mierzy liniowe powiązanie między dwiema zmiennymi x i y . Ma wartość od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Załóżmy na przykład, że mamy następujący zestaw danych zawierający dwie zmienne: (1) przepracowane godziny i (2) wyniki egzaminów uzyskane dla 20 różnych uczniów:

Gdybyśmy stworzyli wykres rozrzutu godzin przepracowanych w porównaniu z wynikami egzaminów, wyglądałoby to tak:

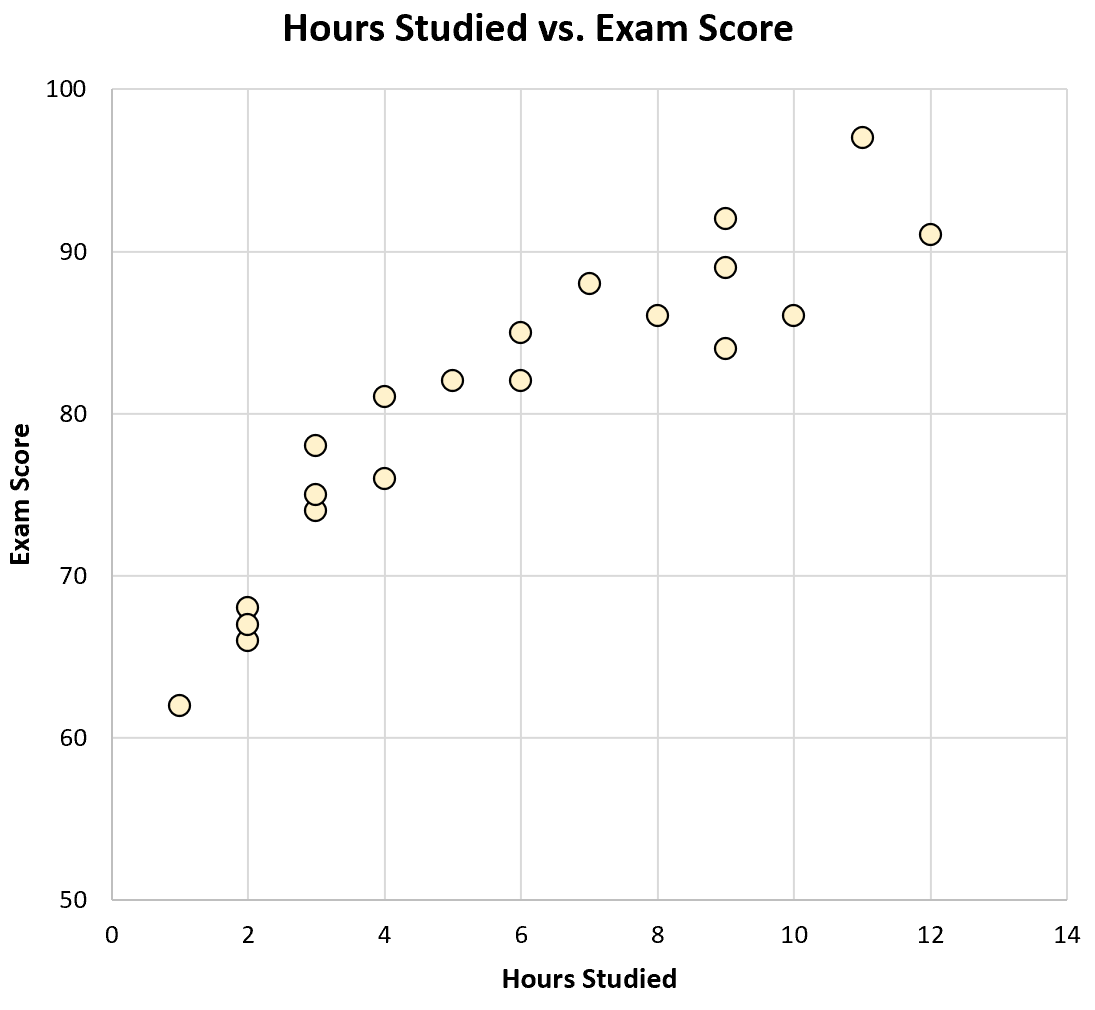
Patrząc na wykres, widzimy, że uczniowie, którzy więcej się uczą, zwykle osiągają lepsze wyniki na egzaminach. Innymi słowy, wizualnie możemy zobaczyć, że istnieje dodatnia korelacja między tymi dwiema zmiennymi.

Korzystając z kalkulatora, możemy zobaczyć, że korelacja między tymi dwiema zmiennymi wynosi r = 0,915 . Wartość ta, będąca bliska 1, potwierdza, że pomiędzy obiema zmiennymi istnieje silna dodatnia korelacja.

Co to jest regresja?

Regresja to metoda, którą możemy zastosować, aby zrozumieć, jak zmiana wartości zmiennej x wpływa na wartości zmiennej y .

Model regresji wykorzystuje jedną zmienną x jako zmienną predykcyjną i drugą zmienną y jakozmienną odpowiedzi . Następnie znajduje równanie w następującej postaci, które najlepiej opisuje związek między dwiema zmiennymi:

ŷ = b ₀ + b ₁ x

Złoto:

• ŷ: przewidywana wartość zmiennej odpowiedzi
• b ₀ : Współrzędna początku układu współrzędnych (wartość y, gdy x jest równe zero)
• b ₁ : Współczynnik regresji (średni wzrost y przy jednostkowym wzroście x)
• x: wartość zmiennej predykcyjnej

Rozważmy na przykład nasz poprzedni zbiór danych:

Korzystając z kalkulatora regresji liniowej , stwierdzamy, że poniższe równanie najlepiej opisuje związek pomiędzy tymi dwiema zmiennymi:

Przewidywany wynik egzaminu = 65,47 + 2,58*(godziny nauki)

Sposób interpretacji tego równania jest następujący:

• Przewidywany wynik egzaminu dla studenta studiującego zero godzin to 65,47 .
• Średni wzrost wyniku z egzaminu związany z dodatkową godziną nauki wynosi 2,58 .

Możemy również użyć tego równania, aby przewidzieć wynik, jaki otrzyma uczeń na podstawie liczby przestudiowanych godzin.

Przykładowo student studiujący 6 godzin powinien otrzymać ocenę 80,95 :

Przewidywany wynik egzaminu = 65,47 + 2,58*(6) = 80,95 .

Możemy również wykreślić to równanie jako linię na wykresie punktowym:

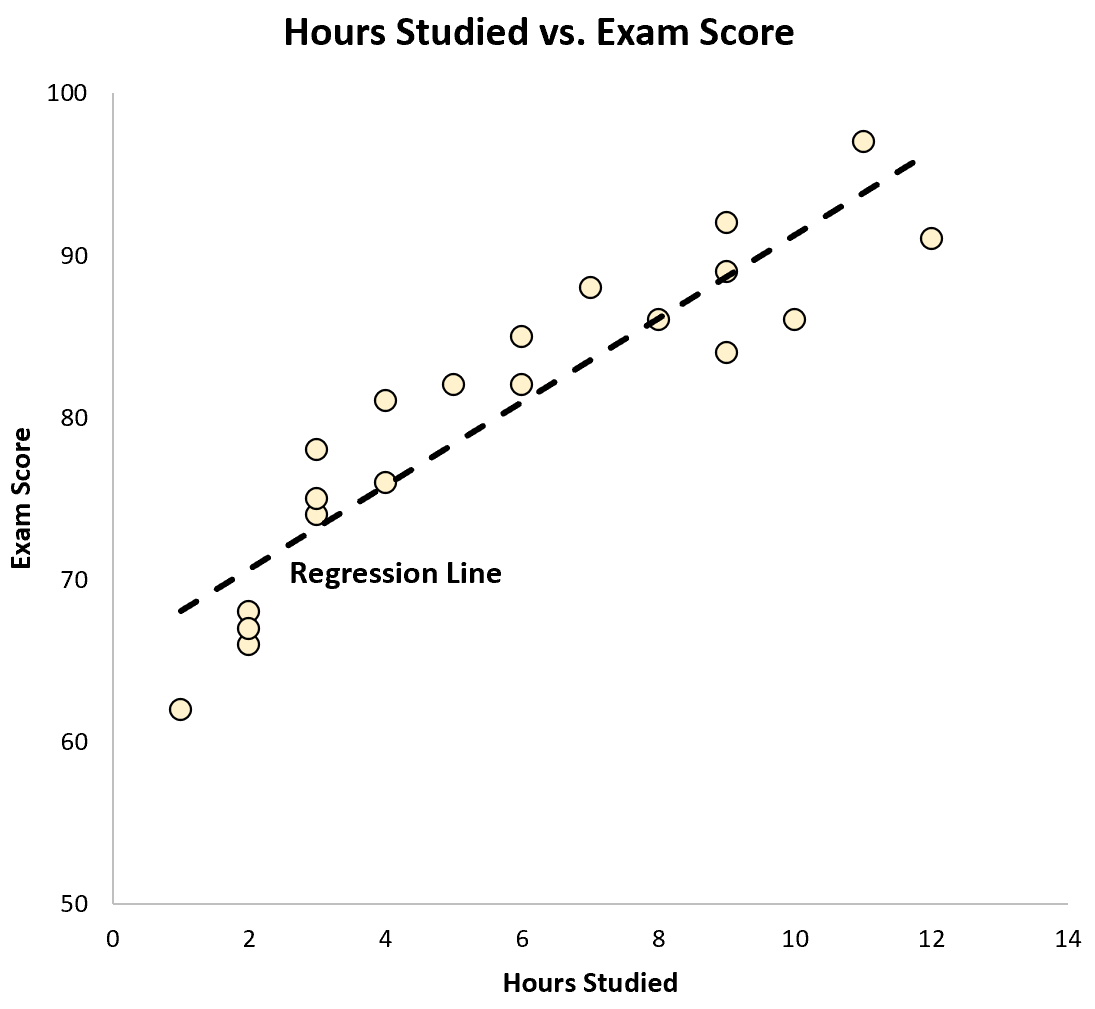
Widzimy, że linia regresji całkiem dobrze „pasuje” do danych.

Przypomnijmy wcześniej, że korelacja między tymi dwiema zmiennymi wynosiła r = 0,915 . Okazuje się, że możemy podnieść tę wartość do kwadratu i otrzymać liczbę zwaną „r do kwadratu”, która opisuje całkowitą część wariancji zmiennej odpowiedzi, którą można wyjaśnić zmienną predykcyjną.

W tym przykładzie r ² = 0,915 ² = 0,837 . Oznacza to, że 83,7% różnic w wynikach egzaminów można wytłumaczyć liczbą godzin nauki.

Korelacja a regresja: podobieństwa i różnice

Oto podsumowanie podobieństw i różnic między korelacją a regresją:

Podobieństwa:

• Obydwa określają ilościowo kierunek związku między dwiema zmiennymi.
• Obydwa określają ilościowo siłę związku między dwiema zmiennymi.

Różnice:

• Regresja jest w stanie wykazać związek przyczynowo-skutkowy pomiędzy dwiema zmiennymi. Korelacja tego nie robi.
• Regresja pozwala na wykorzystanie równania do przewidzenia wartości jednej zmiennej na podstawie wartości innej zmiennej. Korelacja tego nie robi.
• Regresja wykorzystuje równanie do ilościowego określenia związku między dwiema zmiennymi. Korelacja wykorzystuje pojedynczą liczbę.

Dodatkowe zasoby

Poniższe samouczki zawierają bardziej szczegółowe wyjaśnienia tematów poruszonych w tym artykule.

Wprowadzenie do współczynnika korelacji Pearsona
Wprowadzenie do prostej regresji liniowej
Prosty kalkulator regresji liniowej
Jaka jest dobra wartość R-kwadrat?