Korelacja vs. skojarzenie: jaka jest różnica?

Dwa terminy, czasami używane zamiennie, to korelacja i skojarzenie . Jednak w dziedzinie statystyki te dwa terminy mają nieco inne znaczenie.

W szczególności, gdy używamy słowa korelacja , zwykle mówimy o współczynniku korelacji Pearsona . Jest to miara liniowego powiązania pomiędzy dwiema zmiennymi losowymi X i Y. Przyjmuje wartość od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

I odwrotnie, gdy statystycy używają słowa skojarzenie , mogą mówić o dowolnej relacji między dwiema zmiennymi, liniowej lub nieliniowej.

Aby zilustrować tę myśl, rozważmy następujące przykłady.

Wizualizacja korelacji i powiązań z chmurami punktów

Do opisania korelacji pomiędzy dwiema zmiennymi losowymi używamy dwóch słów:

1 kierunek

• Dodatnia: dwie zmienne losowe mają dodatnią korelację, jeśli Y ma tendencję do wzrostu wraz ze wzrostem X.
• Ujemna: dwie zmienne losowe mają ujemną korelację, jeśli Y ma tendencję do zmniejszania się wraz ze wzrostem X.

2. Siła

• Niska: dwie zmienne losowe mają niską korelację, jeśli punkty na wykresie rozrzutu są słabo rozproszone.
• Silna: dwie zmienne losowe mają silną korelację, jeśli punkty na wykresie rozrzutu są blisko siebie zgrupowane.

Poniższe wykresy rozrzutu ilustrują przykłady każdego typu korelacji:

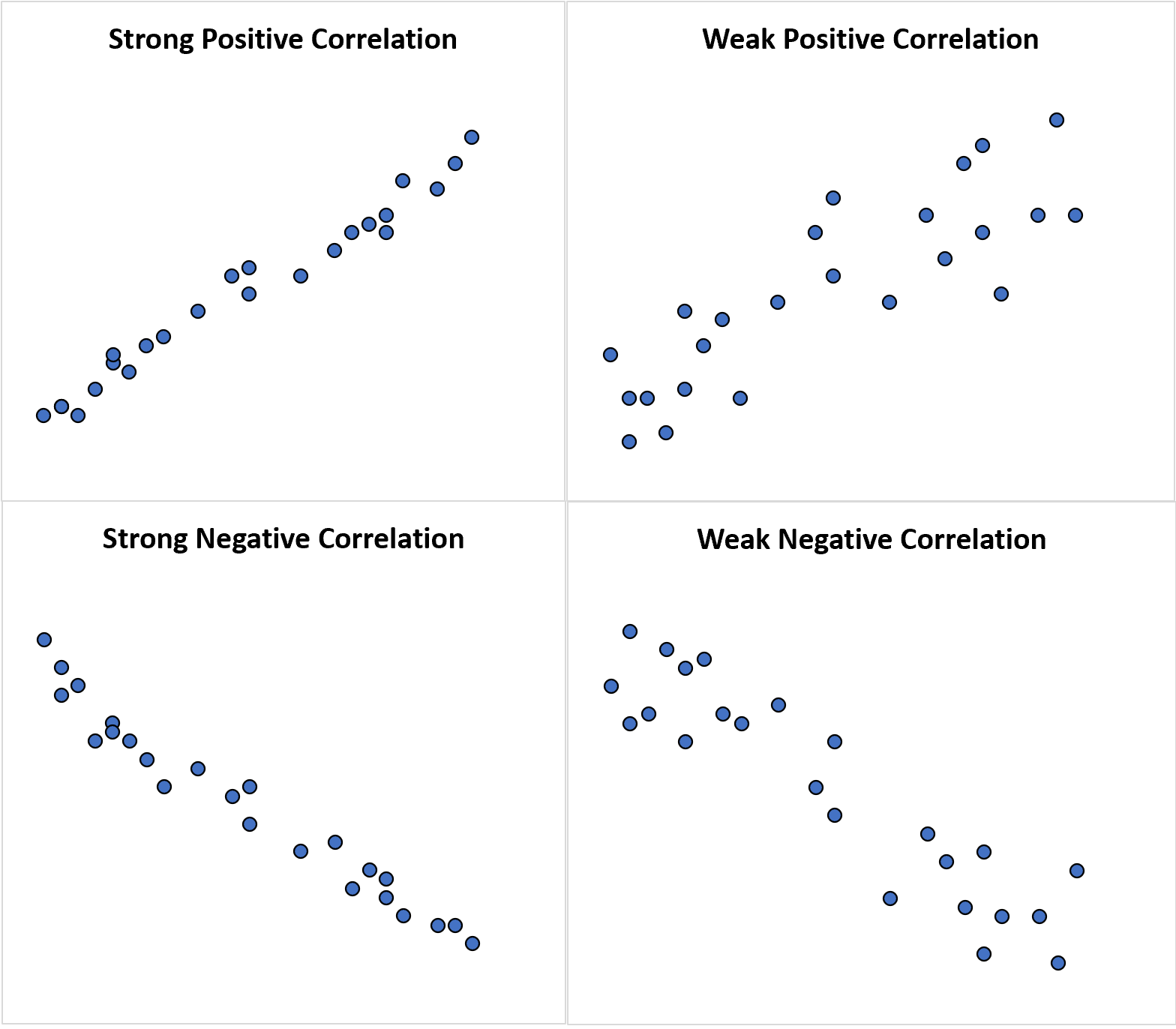
W porównaniu z korelacją słowo skojarzenie może nam powiedzieć, czy istnieje związek między dwiema zmiennymi losowymi: liniowym lub nieliniowym.

Poniższe wykresy punktowe ilustrują kilka przykładów:

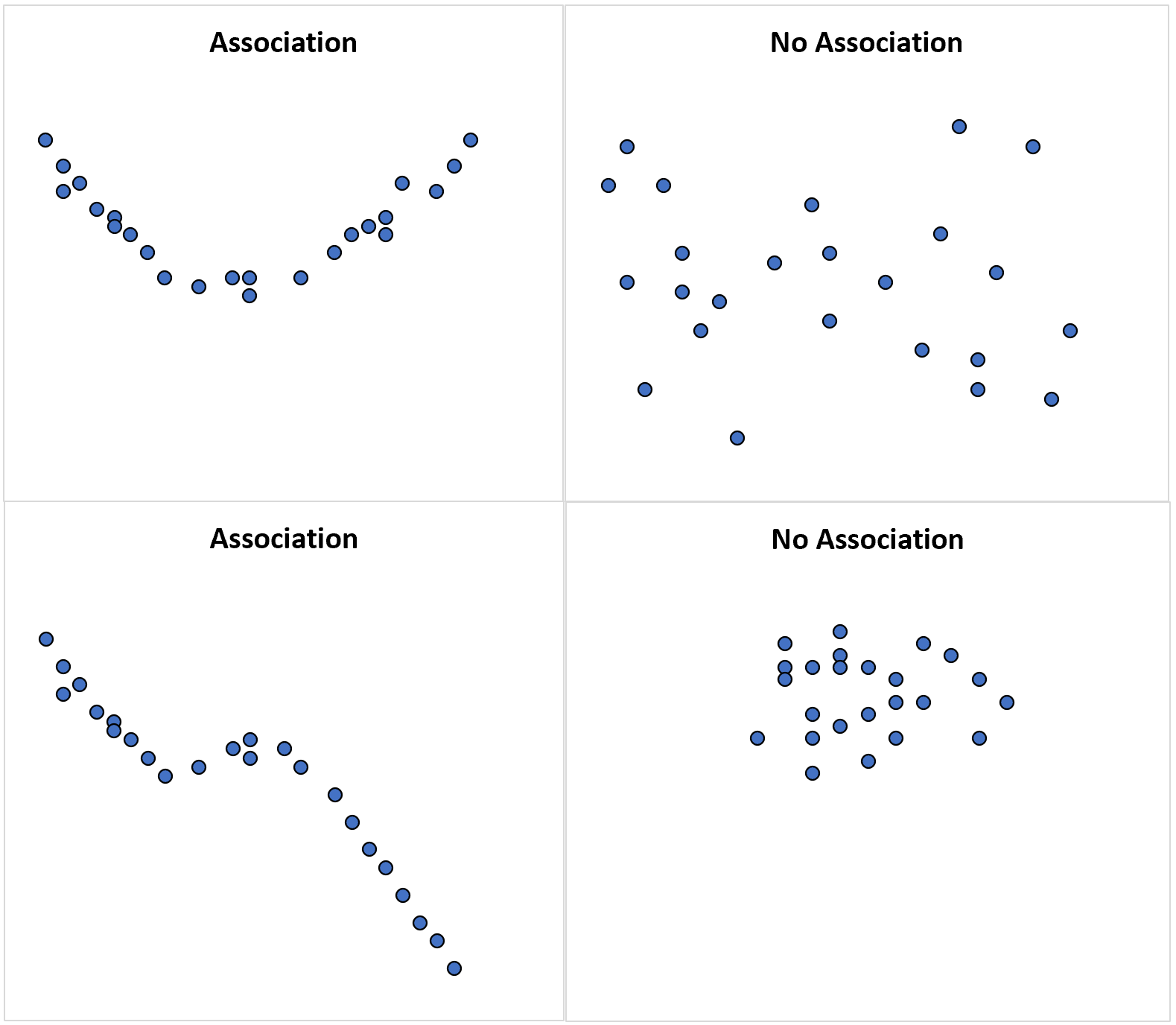
Wykres punktowy w lewym górnym rogu ilustruje zależność kwadratową między dwiema zmiennymi losowymi, co oznacza, że istnieje związek między dwiema zmiennymi, ale nie jest on liniowy.

Gdybyśmy obliczyli korelację między tymi dwiema zmiennymi, prawdopodobnie byłaby ona bliska zeru, ponieważ nie ma między nimi zależności liniowej.

Jednak sama wiedza, że korelacja między dwiema zmiennymi wynosi zero, może wprowadzać w błąd, ponieważ ukrywa fakt, że zamiast tego istnieje zależność nieliniowa.

Korelacja vs. stowarzyszenie: podsumowanie

Terminy korelacja i powiązanie mają następujące podobieństwa i różnice:

Podobieństwa:

• Obydwa terminy są używane do opisania, czy istnieje związek między dwiema zmiennymi losowymi.
• W obu terminach można wykorzystać wykresy rozrzutu do analizy związku między dwiema zmiennymi losowymi.

Różnice:

• Korelacja może nam jedynie powiedzieć, czy dwie zmienne losowe mają związek liniowy, podczas gdy skojarzenie może nam powiedzieć, czy dwie zmienne losowe mają związek liniowy czy nieliniowy.
• Korelacja określa ilościowo związek między dwiema zmiennymi losowymi przy użyciu liczby od -1 do 1, ale powiązanie nie wykorzystuje konkretnej liczby do ilościowego określenia związku.

Dodatkowe zasoby

Wprowadzenie do współczynnika korelacji Pearsona
Wprowadzenie do chmur punktów
Korelacja a regresja: jaka jest różnica?