Jak obliczyć korelację w sas-ie (z przykładami)

Jednym ze sposobów ilościowego określenia związku między dwiema zmiennymi jest użycie współczynnika korelacji Pearsona , który mierzy liniowy związek między dwiema zmiennymi .

Zawsze przyjmuje wartość z zakresu od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Im współczynnik korelacji jest bardziej od zera, tym silniejszy jest związek między obiema zmiennymi.

Poniższe przykłady pokazują, jak używać proc corr w SAS do obliczenia współczynnika korelacji między zmiennymi w zintegrowanym zbiorze danych SAS o nazwie Fish , który zawiera różne pomiary dla 159 różnych ryb złowionych w jeziorze w Finlandii.

Możemy użyć proc print do wyświetlenia pierwszych 10 obserwacji tego zbioru danych:

 /*view first 10 observations from Fish dataset*/
proc print data =sashelp.Fish( obs = 10 );

run ;

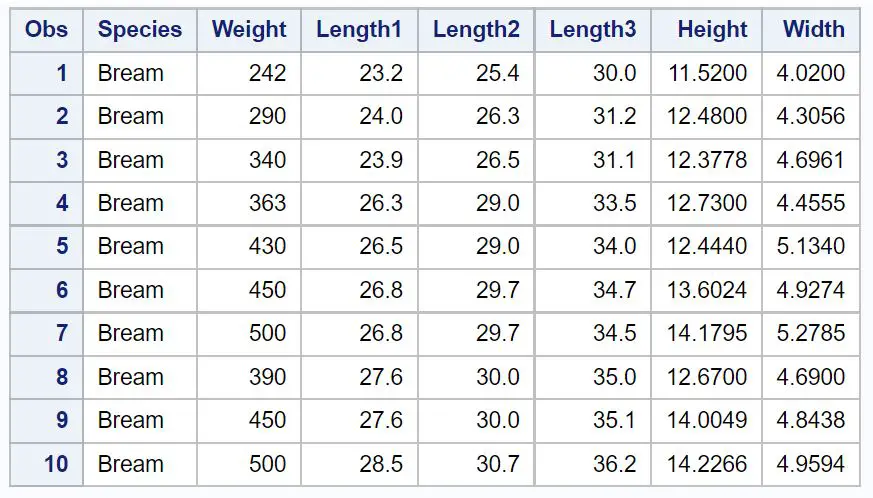
Przykład 1: Korelacja między dwiema zmiennymi

Możemy użyć poniższego kodu do obliczenia współczynnika korelacji Pearsona pomiędzy zmiennymi Wysokość i Szerokość:

 /*calculate correlation coefficient between Height and Width*/
proc corr data =sashelp.fish;
	var HeightWidth;

run ;

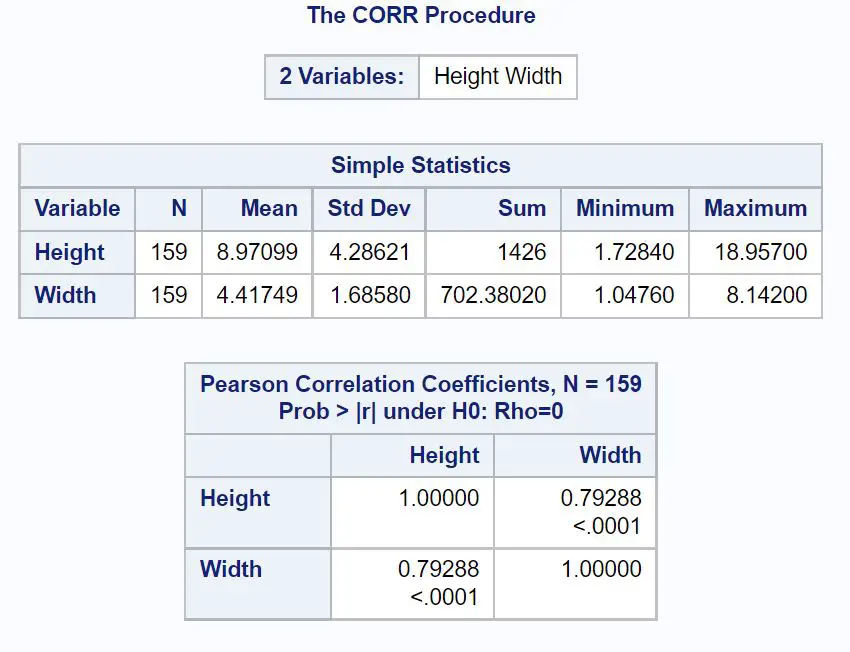
Pierwsza tabela wyświetla podsumowanie statystyk dotyczących wysokości i szerokości.

Druga tabela przedstawia współczynnik korelacji Pearsona pomiędzy dwiema zmiennymi, łącznie z wartością p , która mówi nam, czy korelacja jest istotna statystycznie.

Z wyniku możemy zobaczyć:

• Współczynnik korelacji Pearsona: 0,79288
• Wartość P: <0,0001

To mówi nam, że istnieje silna dodatnia korelacja między wysokością a szerokością i że korelacja jest istotna statystycznie, ponieważ wartość p jest mniejsza niż α = 0,05.

Powiązane: Co uważa się za „silną” korelację?

Przykład 2: Korelacja pomiędzy wszystkimi zmiennymi

Możemy użyć poniższego kodu, aby obliczyć współczynnik korelacji Pearsona pomiędzy wszystkimi parami kombinacji zmiennych w zbiorze danych:

 /*calculate correlation coefficient between all pairwise combinations of variables*/
proc corr data =sashelp.fish;

run;

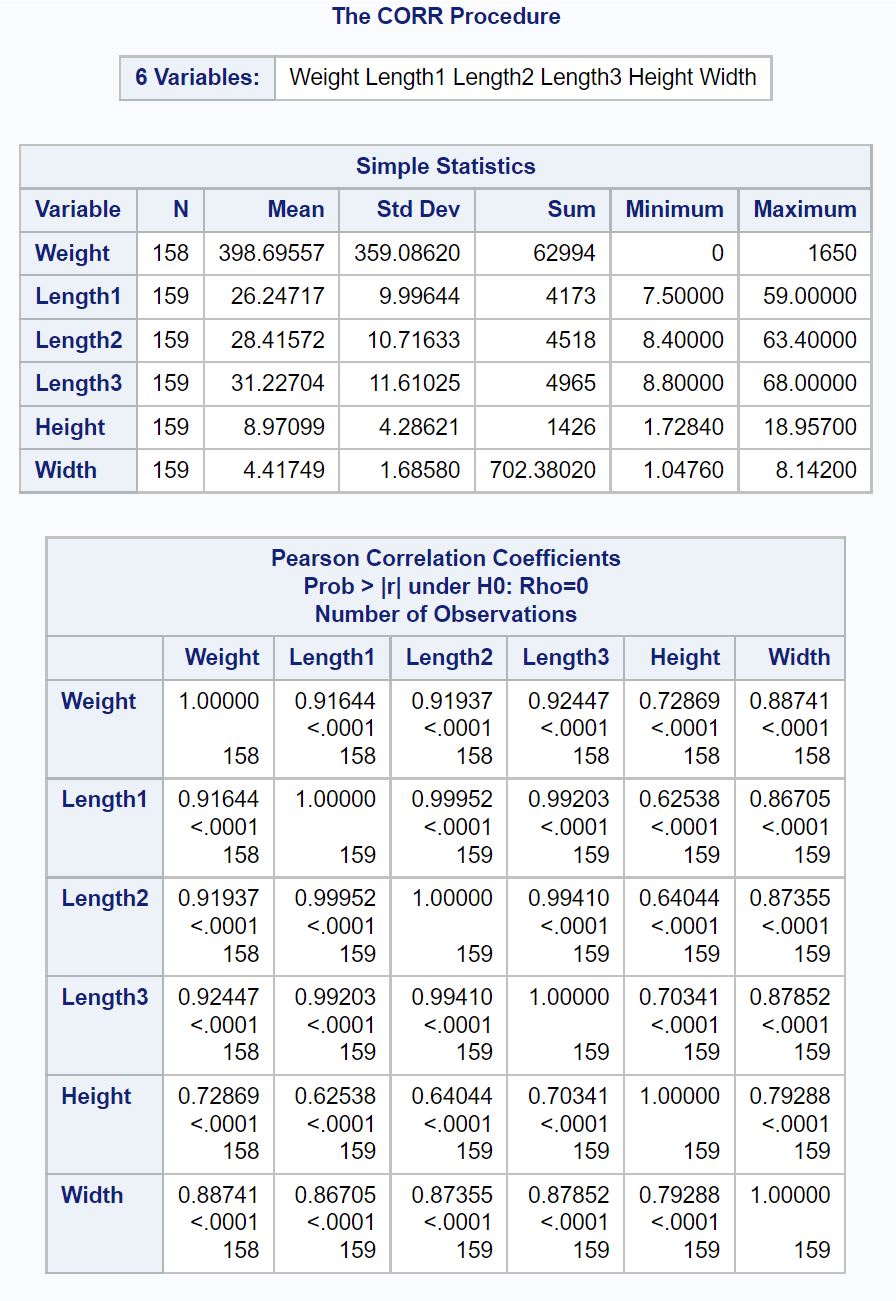
Wynik wyświetla macierz korelacji , która zawiera współczynnik korelacji Pearsona i odpowiadające mu wartości p dla każdej pary kombinacji zmiennych numerycznych w zbiorze danych.

Na przykład:

• Współczynnik korelacji Pearsona między masą a długością1 wynosi 0,91644.
• Współczynnik korelacji Pearsona między masą a długością2 wynosi 0,91937.
• Współczynnik korelacji Pearsona między masą a długością3 wynosi 0,92447.

I tak dalej.

Przykład 3: Wizualizuj korelację za pomocą wykresu rozrzutu

Możemy również użyć funkcji plots , aby utworzyć wykres rozrzutu w celu wizualizacji korelacji między dwiema zmiennymi:

 /*visualize correlation between Height and Width*/
proc corr data =sashelp.fish plots =scatter( nvar =all);;
	var HeightWidth;

run; 

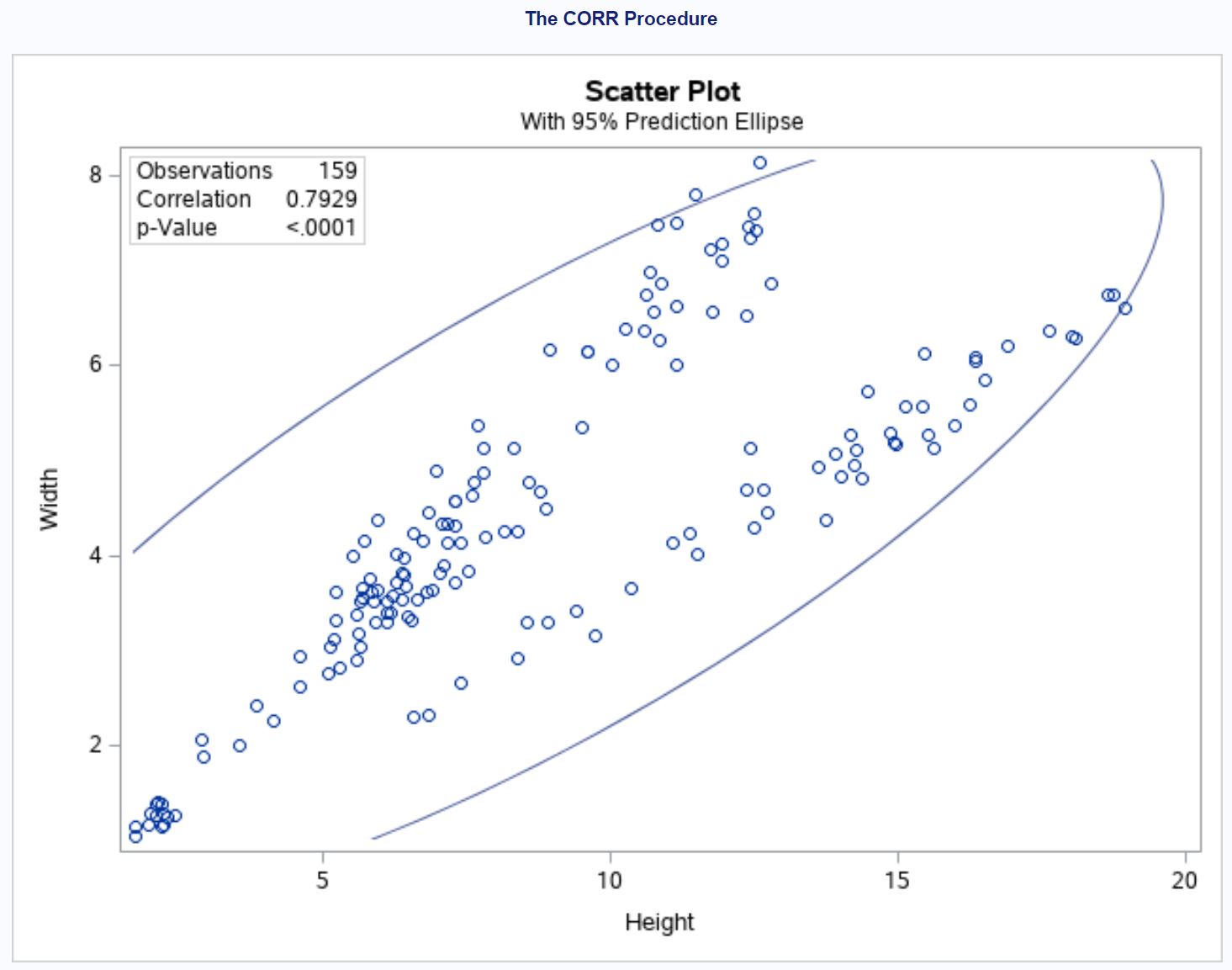
Na wykresie widać silną dodatnią korelację pomiędzy wysokością a szerokością. Wraz ze wzrostem wysokości zwiększa się również szerokość.

W lewym górnym rogu wykresu widać także całkowitą liczbę wykorzystanych obserwacji, współczynnik korelacji oraz wartość p współczynnika korelacji.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak wykonywać inne typowe operacje w SAS-ie:

Jak tworzyć tabele częstości w SAS-ie
Jak obliczyć statystyki opisowe w SAS-ie