Korelacje w stata: pearson, spearman i kendall

W statystyce korelacja odnosi się do siły i kierunku związku między dwiema zmiennymi. Wartość współczynnika korelacji może mieścić się w zakresie od -1 do 1, gdzie -1 oznacza idealną ujemną zależność, 0 oznacza brak związku, a 1 oznacza doskonałą dodatnią zależność.

Istnieją trzy popularne sposoby pomiaru korelacji:

Korelacja Pearsona: Służy do pomiaru korelacji między dwiema zmiennymi ciągłymi. (np. wzrost i waga)

Korelacja Spearmana: Służy do pomiaru korelacji między dwiema sklasyfikowanymi zmiennymi. (np. ranking wyników ucznia z egzaminu z matematyki w porównaniu z rankingiem jego wyników z egzaminu z przedmiotów ścisłych w klasie)

Korelacja Kendalla: Używana, gdy chcesz zastosować korelację Spearmana, ale wielkość próby jest mała i istnieje wiele powiązanych rankingów.

W tym samouczku wyjaśniono, jak znaleźć trzy typy korelacji w Stata.

Ładowanie danych

W każdym z poniższych przykładów użyjemy zbioru danych o nazwie auto . Możesz załadować ten zestaw danych, wpisując następujące polecenie w polu Polecenie:

użyj https://www.stata-press.com/data/r13/auto

Możemy uzyskać szybki przegląd zbioru danych, wpisując następujące polecenie w polu poleceń:

podsumować

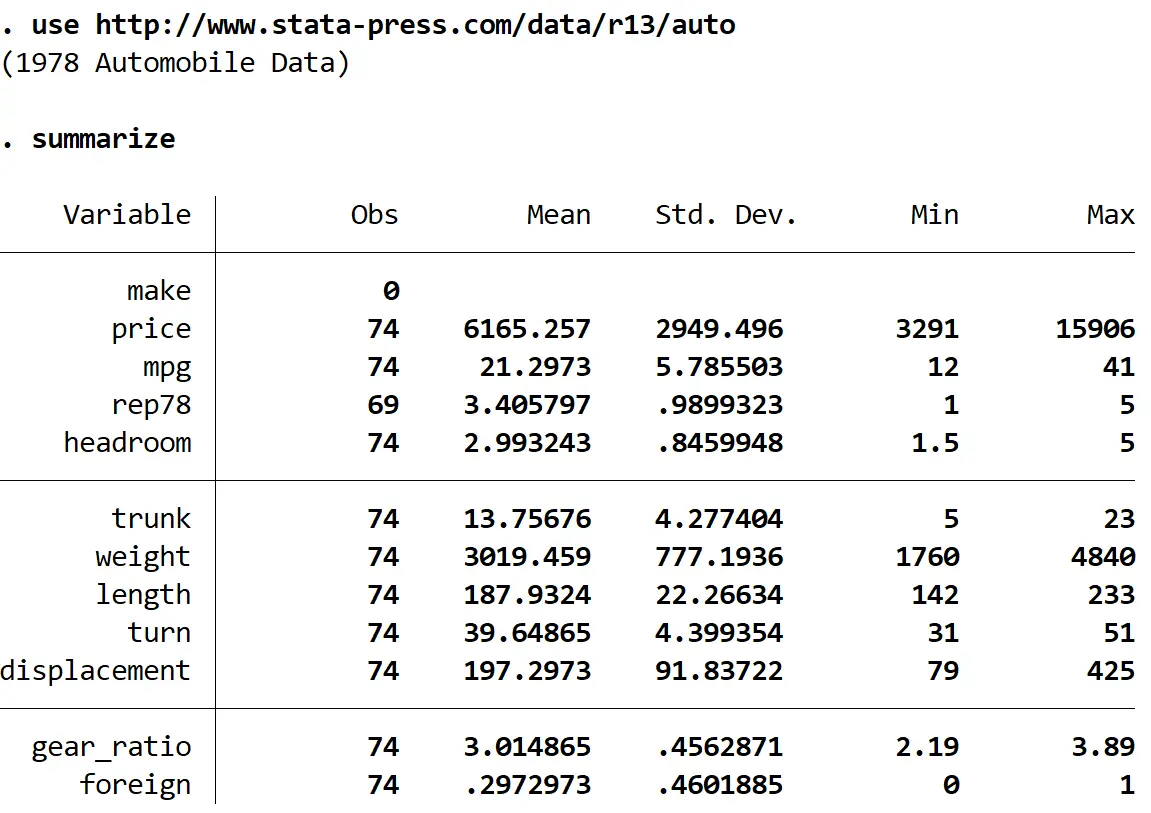
Widzimy, że w zbiorze danych znajduje się łącznie 12 zmiennych.

Jak znaleźć korelację Pearsona w Stata

Współczynnik korelacji Pearsona pomiędzy zmiennymi wagi i długości możemy znaleźć za pomocą polecenia pwcorr :

pwcorr długość wagi

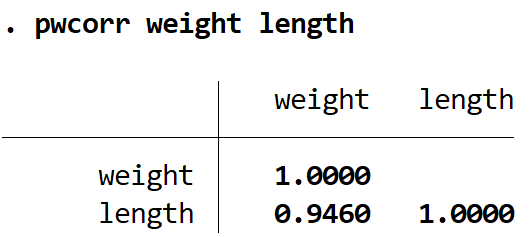
Współczynnik korelacji Pearsona pomiędzy tymi dwiema zmiennymi wynosi 0,9460 . Aby określić, czy ten współczynnik korelacji jest istotny, możemy znaleźć wartość p za pomocą polecenia sig :

pwcorr długość ciężaru, sig

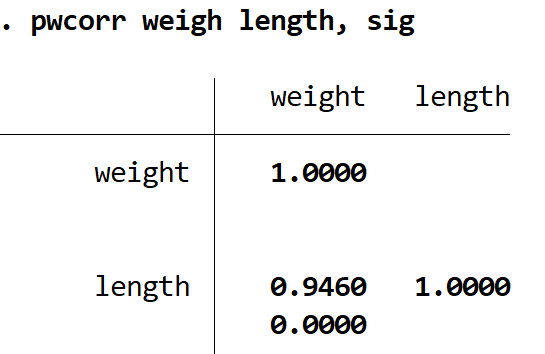
Wartość p wynosi 0,000 . Ponieważ jest to mniej niż 0,05, korelacja między tymi dwiema zmiennymi jest istotna statystycznie.

Aby znaleźć współczynnik korelacji Pearsona dla wielu zmiennych, po prostu wpisz listę zmiennych po poleceniu pwcorr :

pwcorr przemieszczenie długości ciężarka, sig

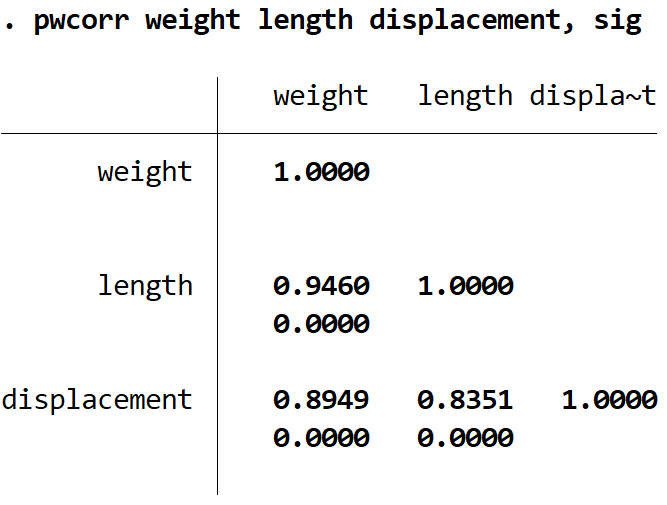
Oto jak zinterpretować wynik:

• Korelacja Pearsona między masą a długością = 0,9460 | wartość p = 0,000
• Korelacja Pearsona między masą a przemieszczeniem = 0,8949 | wartość p = 0,000
• Korelacja Pearsona pomiędzy przemieszczeniem a długością = 0,8351 | wartość p = 0,000

Jak znaleźć korelację Spearmana w Stata

Możemy znaleźć współczynnik korelacji Spearmana pomiędzy zmiennymi trunk i rep78 za pomocą polecenia spearman :

lanca tułowia rep78

Oto jak zinterpretować wynik:

• Liczba obs: Jest to liczba obserwacji parami używana do obliczenia współczynnika korelacji Spearmana. Ponieważ dla zmiennej rep78 brakowało niektórych wartości, Stata wykorzystał jedynie 69 obserwacji na parę (zamiast pełnych 74).
• Rho Spearmana: Jest to współczynnik korelacji Spearmana. W tym przypadku jest to -0,2235, co oznacza, że pomiędzy obiema zmiennymi istnieje ujemna korelacja. Gdy jedno rośnie, drugie ma tendencję do zmniejszania się.
• Prawdopodobne > |t| : Jest to wartość p powiązana z testem hipotezy. W tym przypadku wartość p wynosi 0,0649, co oznacza, że nie ma statystycznie istotnej korelacji pomiędzy obiema zmiennymi przy α = 0,05.

Możemy znaleźć współczynnik korelacji Spearmana dla wielu zmiennych, po prostu wpisując więcej zmiennych po poleceniu spearmana . Możemy znaleźć współczynnik korelacji i odpowiednią wartość p dla każdej korelacji parami za pomocą polecenia stats(rho p) :

włócznia tułowia rep78 gear_ratio, statystyki (rho p)

Oto jak zinterpretować wynik:

• Korelacja Spearmana między tułowiem a rep78 = -0,2235 | wartość p = 0,0649
• Korelacja Spearmana między pniem a współczynnikiem biegów = -0,5187 | wartość p = 0,0000
• Korelacja Spearmana pomiędzy gear_ratio i rep78 = 0,4275 | wartość p = 0,0002

Jak znaleźć korelację Kendalla w Stata

Możemy znaleźć współczynnik korelacji Kendalla pomiędzy zmiennymi trunk i rep78 za pomocą polecenia ktau :

ktau pnia rep78

Oto jak zinterpretować wynik:

• Liczba obs: Jest to liczba obserwacji parami używana do obliczenia współczynnika korelacji Kendalla. Ponieważ dla zmiennej rep78 brakowało niektórych wartości, Stata wykorzystał jedynie 69 obserwacji na parę (zamiast pełnych 74).
• Tau-b Kendalla: Jest to współczynnik korelacji Kendalla między dwiema zmiennymi. Zwykle używamy tej wartości zamiast tau-a, ponieważ tau-b dokonuje korekt w przypadku remisu. W tym przypadku tau-b = -0,1752, co wskazuje na ujemną korelację pomiędzy obiema zmiennymi.
• Prawdopodobne > |z| : Jest to wartość p powiązana z testem hipotezy. W tym przypadku wartość p wynosi 0,0662, co oznacza, że nie ma statystycznie istotnej korelacji pomiędzy obiema zmiennymi przy α = 0,05.

Możemy znaleźć współczynnik korelacji Kendalla dla wielu zmiennych, po prostu wpisując więcej zmiennych po poleceniu ktau . Możemy znaleźć współczynnik korelacji i odpowiednią wartość p dla każdej korelacji parami za pomocą polecenia stats(taub p) :

ktau bagażnik rep78 gear_ratio, statystyki (taub p)

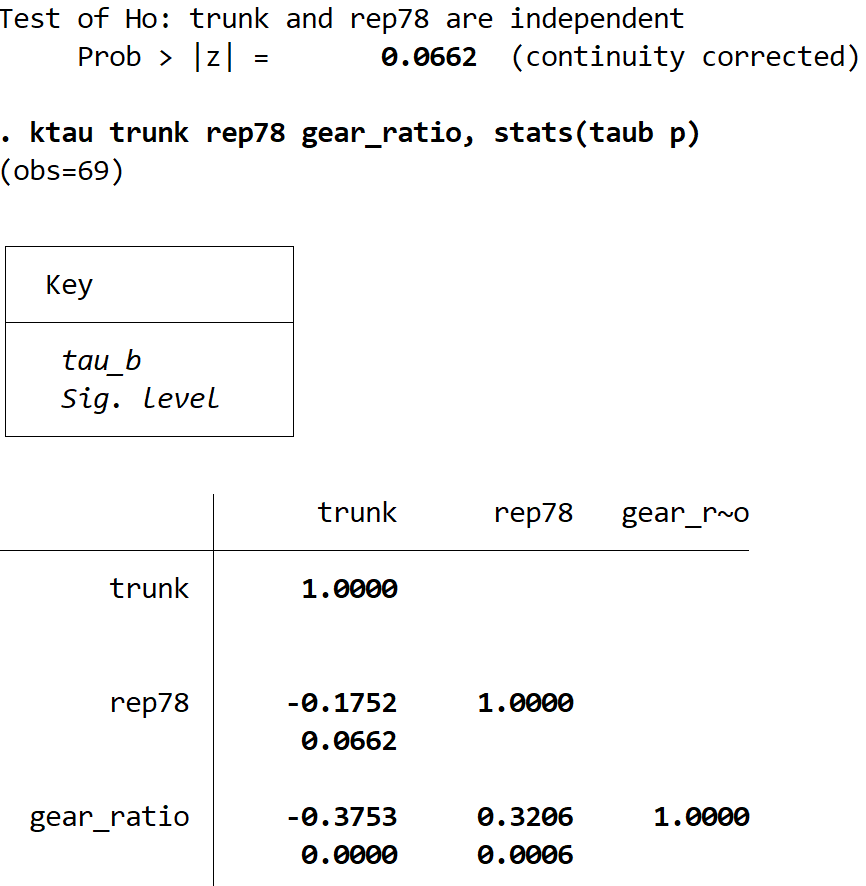
• Korelacja Kendalla między tułowiem a rep78 = -0,1752 | wartość p = 0,0662
• Korelacja Kendalla między bagażnikiem a współczynnikiem przekładni = -0,3753 | wartość p = 0,0000
• Korelacja Kendalla pomiędzy gear_ratio i rep78 = 0,3206 | wartość p = 0,0006