Kowariancja

Przez Benjamin Anderson 5 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest kowariancja i jak jest obliczana. Znajdziesz tu wzór na kowariancję oraz przykład obliczania kowariancji zbioru danych. Dodatkowo możesz obliczyć kowariancję dowolnej serii danych za pomocą kalkulatora online na końcu.

Co to jest kowariancja?

W statystyce kowariancja jest wartością wskazującą stopień łącznej zmienności dwóch zmiennych losowych. Innymi słowy, kowariancję wykorzystuje się do analizy zależności między dwiema zmiennymi.

Kowariancja jest równa sumie iloczynów różnic między danymi dwóch zmiennych i ich odpowiednich średnich podzielonej przez całkowitą liczbę danych.

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć kowariancję dowolnego zbioru danych.

Interpretacja wartości kowariancji jest bardzo prosta:

Jeśli kowariancja jest dodatnia , oznacza to, że istnieje zależność pomiędzy dwiema zmiennymi. Dlatego też, gdy wartość jednej zmiennej wzrasta, druga zmienna również wzrasta i odwrotnie.
Jeśli kowariancja jest ujemna , oznacza to, że związek między dwiema zmiennymi jest ujemny. Tak więc, gdy wartość jednej zmiennej wzrasta, druga maleje i odwrotnie.
Jeżeli kowariancja wynosi zero (lub jej wartość jest bliska zeru), oznacza to, że nie ma związku pomiędzy obiema zmiennymi. Innymi słowy, dwie zmienne losowe są niezależne.

Jak obliczyć kowariancję

Aby obliczyć kowariancję serii danych, należy wykonać następujące kroki:

Oblicz średnią dla każdej zmiennej osobno.
Dla każdej zmiennej znajdź różnicę między każdą jej wartością a średnią zmiennej.
Pomnóż różnice obliczone w poprzednim kroku dla każdego punktu danych.
Dodaj wszystkie wyniki uzyskane w poprzednim kroku.
Podziel przez całkowitą liczbę danych. Uzyskana wartość jest kowariancją serii danych.

Podsumowując, wzór na obliczenie kowariancji między dwiema zmiennymi jest następujący:

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

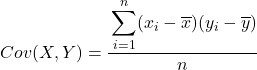
Zdecydowanie zalecaną metodą wyodrębnienia kowariancji między dwiema zmiennymi jest utworzenie tabeli zawierającej wszystkie pary danych i dodanie kolumny dla każdego z opisanych powyżej kroków. W ten sposób Twoje obliczenia będą znacznie lepiej zorganizowane i lepiej zrozumiesz, co robisz.

Przykład obliczenia kowariancji

Biorąc pod uwagę definicję kowariancji, poniżej znajduje się przykład krok po kroku obliczania tego typu miary statystycznej. Celem jest lepsze zrozumienie pojęcia kowariancji i sposobu analizowania korelacji między dwiema zmiennymi.

Oblicz kowariancję następującego zbioru danych statystycznych:

Najpierw musimy obliczyć średnią arytmetyczną każdej zmiennej. Aby to zrobić, dzielimy sumę wartości każdej zmiennej przez całkowitą liczbę danych.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ Zobacz: średnia ze wzoru arytmetycznego

Po określeniu średniej każdej zmiennej losowej możemy dodać następujące kolumny do tabeli danych, aby uzyskać kowariancję:

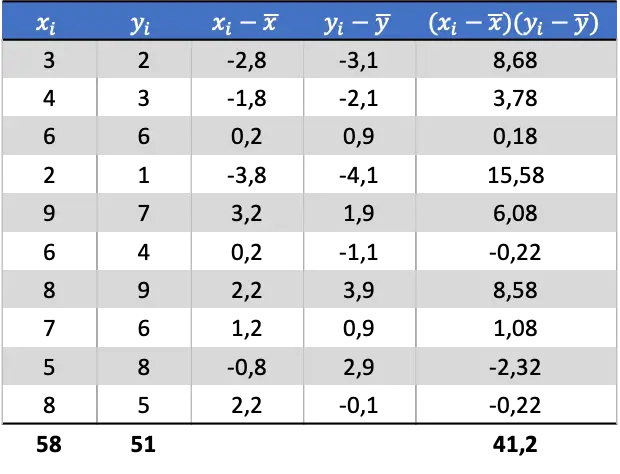
Aby więc określić kowariancję obu zmiennych, należy podzielić sumę ostatniej kolumny przez liczbę par danych:

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

W tym przypadku wartość kowariancji jest dodatnia, co oznacza, że pomiędzy dwiema badanymi zmiennymi losowymi istnieje bezpośrednia zależność. Jeżeli jednak wartość kowariancji byłaby ujemna, oznaczałoby to, że zależność pomiędzy obiema zmiennymi jest odwrotna. I wreszcie, jeśli wartość kowariancji wynosi zero lub jest bardzo bliska zeru, oznacza to, że między dwiema zmiennymi nie ma liniowej zależności.

Jak widać po rozwiązaniu tego przykładu, bardzo przydatne jest skorzystanie z programu komputerowego takiego jak Excel, aby dodać kolumny do tabeli i szybko wykonać obliczenia. W przeciwnym razie, obliczając operacje ręcznie, znalezienie kowariancji zajmie znacznie więcej czasu.

Kalkulator kowariancji

Wprowadź zestaw danych statystycznych do poniższego kalkulatora, aby obliczyć kowariancję między dwiema zmiennymi. Należy rozdzielić pary danych tak, aby w pierwszym polu znajdowały się tylko wartości jednej zmiennej, a w drugim tylko wartości drugiej zmiennej.

Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.

Właściwości kowariancji

Kowariancja ma następujące właściwości:

Kowariancja między zmienną losową a stałą wynosi zero.

$Cov(X,a)=0$

Kowariancja zmiennej i sama w sobie jest równoważna wariancji tej zmiennej.

$Cov(X,X)=Var(X)$

➤ Zobacz: czym jest wariancja?

Kowariancja spełnia własność symetrii, zatem kowariancja zmiennych X i Y jest równa kowariancji zmiennych Y i X. Kolejność zmiennych nie ma wpływu na wynik kowariancji.

$Cov(X,Y)=Cov(Y,X)$

Jeśli zmienne są mnożone przez stałe, można najpierw obliczyć kowariancję, a następnie pomnożyć wynik przez stałe.

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

Dodanie terminów do zmiennych nie ma wpływu na wynik kowariancji.

$Cov(a+X,b+Y)=Cov(X+Y)$

Kowariancja między dwiema zmiennymi losowymi jest powiązana z ich oczekiwaniami matematycznymi. Kowariancja między zmiennymi X i Y jest równa oczekiwaniu matematycznemu iloczynu X i Y minus iloczyn oczekiwań matematycznych każdej zmiennej.

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

Podczas pracy ze zmiennymi następujące wyrażenie algebraiczne jest wypełniane w odniesieniu do kowariancji:

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej