Kryterium chauveneta: definicja i przykład

Wartość odstająca to obserwacja , która jest nienormalnie odległa od innych wartości w zbiorze danych. Wartości odstające mogą być problematyczne, ponieważ mogą wpływać na wyniki analizy.

Jednym ze sposobów identyfikacji wartości odstających w zbiorze danych jest użycie kryterium Chauveneta , które wykorzystuje następujący proces:

1. Dla każdej indywidualnej wartości x _i w zbiorze danych oblicz odchylenie od średniej w następujący sposób:

Odchylenie = |x _i – x | /S

gdzie x to średnia próbki, a s to odchylenie standardowe próbki.

2. Porównaj odchylenia każdej indywidualnej wartości z wartościami krytycznymi w poniższej tabeli kryteriów Chauveneta. W przypadku poszczególnych wartości danych z odchyleniami większymi niż te znajdujące się w tabeli, należy zgłosić te wartości danych jako wartości odstające.

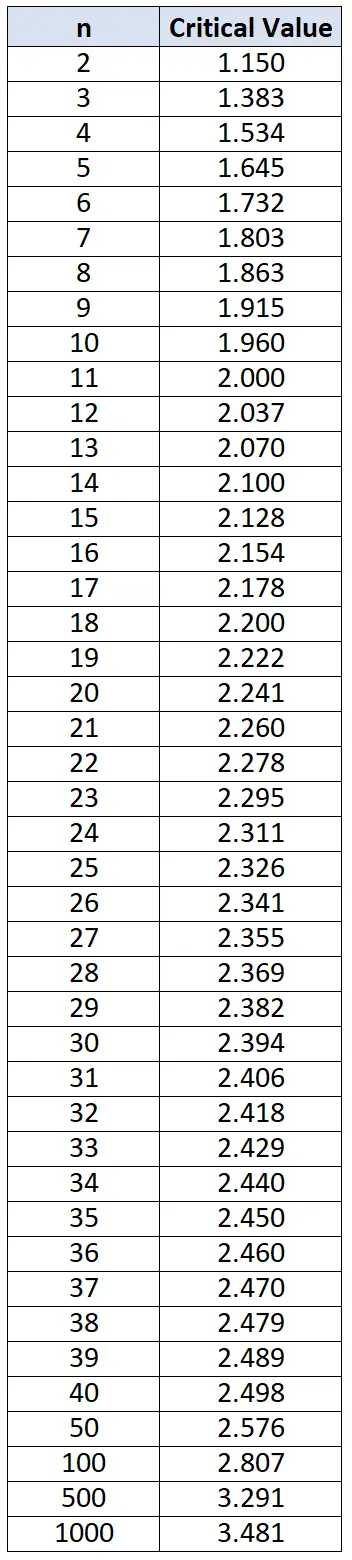
Kryterium Chauveneta: przykład

Załóżmy, że mamy następujący zestaw danych składający się z 15 wartości:

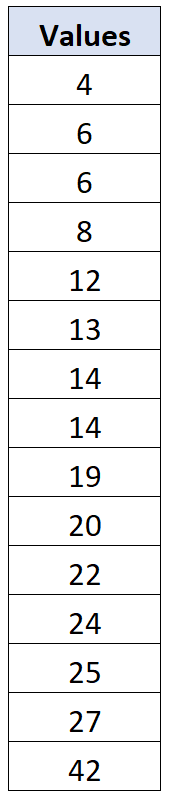
Średnia próbki dla tego zbioru danych wynosi x = 17,067 , a odchylenie standardowe próbki wynosi s = 10,096 . Dla każdej indywidualnej wartości danych możemy obliczyć jej odchylenie w następujący sposób:

Odchylenie = |x _i – x | /S

Na przykład:

• Pierwsza wartość danych miałaby odchylenie |4 – 17,067| / 10096 = 1294 .
• Pierwsza wartość danych miałaby odchylenie |6 – 17,067| / 10,096 = 1,096 .

I tak dalej.

Możemy użyć tego samego wzoru do obliczenia odchylenia każdej indywidualnej wartości danych:

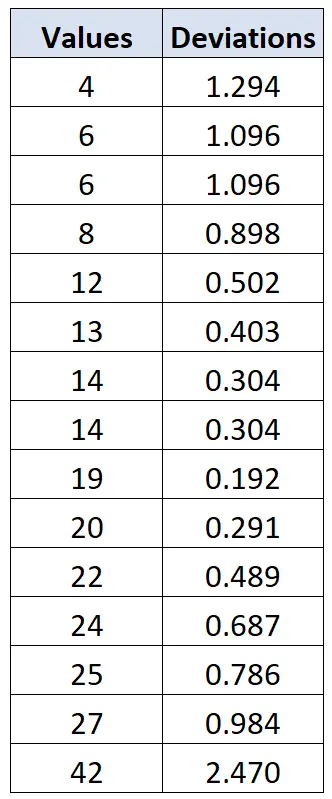
Możemy następnie odwołać się do tabeli kryteriów Chauveneta i zauważyć, że wartość krytyczna odpowiadająca wielkości próby n=15 wynosi 2,128 . Zatem każdą wartość z odchyleniem większym niż 2,128 można uznać za wartość odstającą.

Okazuje się, że wartość 42 ma odchylenie większe niż 2,128:

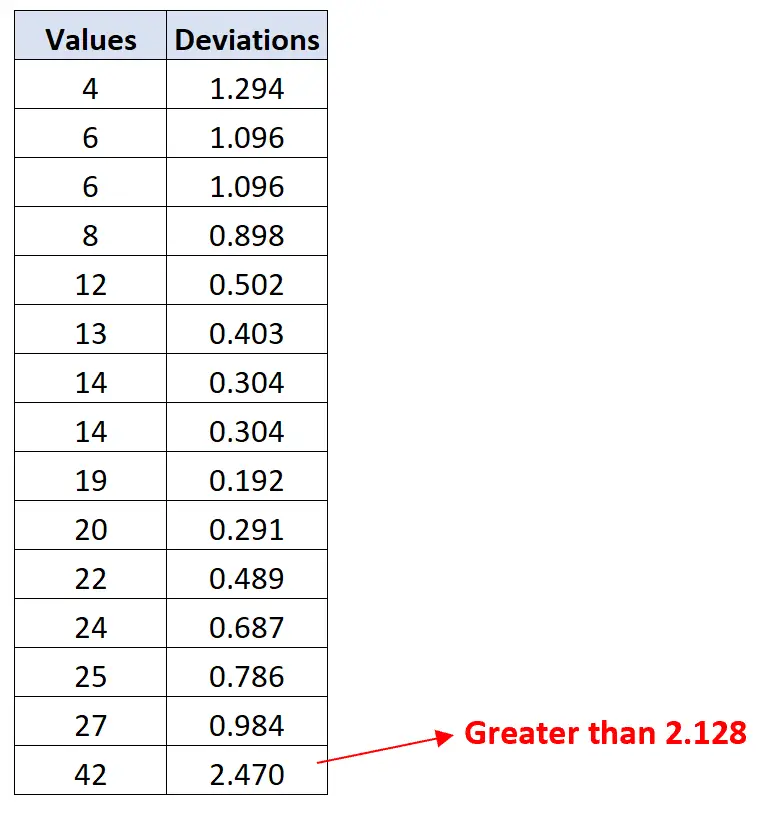
Zatem wartość 42 jest jedyną wartością odstającą w tym zbiorze danych.

Środki ostrożności dotyczące stosowania kryterium Chauveneta

Kryterium Chauveneta zakłada, że wartości w zbiorze danych mają rozkład normalny . Jeżeli to założenie nie jest spełnione, użycie kryterium Chauveneta do identyfikacji wartości odstających prawdopodobnie nie będzie prawidłowe.

Jeśli użyjesz tej metody i stwierdzisz, że wartość jest wartością odstającą, musisz najpierw sprawdzić, czy wartość nie jest wynikiem błędu we wprowadzaniu danych. Czasami dane są po prostu wprowadzane błędnie.

Jeśli wartość rzeczywiście odbiega od normy, możesz ją usunąć, jeśli będzie miała znaczący wpływ na ogólną analizę. Pamiętaj tylko, aby podczas raportowania wyników wspomnieć, że usunąłeś wartość odstającą.

Ponadto tę metodę należy zastosować tylko raz na danym zbiorze danych. Załóżmy na przykład, że użyjemy tego kryterium do zidentyfikowania wartości 42 jako wartości odstającej w poprzednim przykładzie i usunięcia tej wartości ze zbioru danych.

Nie powinniśmy wówczas ponownie obliczać średniej próbki i odchylenia standardowego próbki i ponownie obliczać odchylenia, aby znaleźć więcej wartości odstających.