Co to są krzywe gęstości? (wyjaśnienie i przykłady)

Krzywa gęstości to krzywa na wykresie przedstawiająca rozkład wartości w zestawie danych. Jest to przydatne z trzech powodów:

1. Krzywa gęstości daje nam dobre wyobrażenie o „kształcie” rozkładu, w tym o tym, czy rozkład ma jeden lub więcej „szczytów” wartości częstotliwości oraz czy rozkład jest przesunięty w lewo lub prawo. PRAWIDŁOWY. .

2. Krzywa gęstości pozwala nam wizualnie zobaczyć, gdzie powiązana jest średnia i mediana rozkładu.

3. Krzywa gęstości pozwala nam wizualnie zobaczyć, jaki procent obserwacji w zbiorze danych mieści się pomiędzy różnymi wartościami.

Najbardziej znaną krzywą gęstości jest krzywa w kształcie dzwonu, która reprezentuje rozkład normalny .

Aby lepiej zrozumieć krzywe gęstości, rozważ następujący przykład.

Przykład: tworzenie i interpretacja krzywej gęstości

Załóżmy, że mamy następujący zbiór danych, który pokazuje wysokość 20 różnych roślin (w calach) na określonym polu:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Gdybyśmy utworzyli prosty histogram do wyświetlenia względnych częstotliwości każdej wartości, wyglądałby tak:

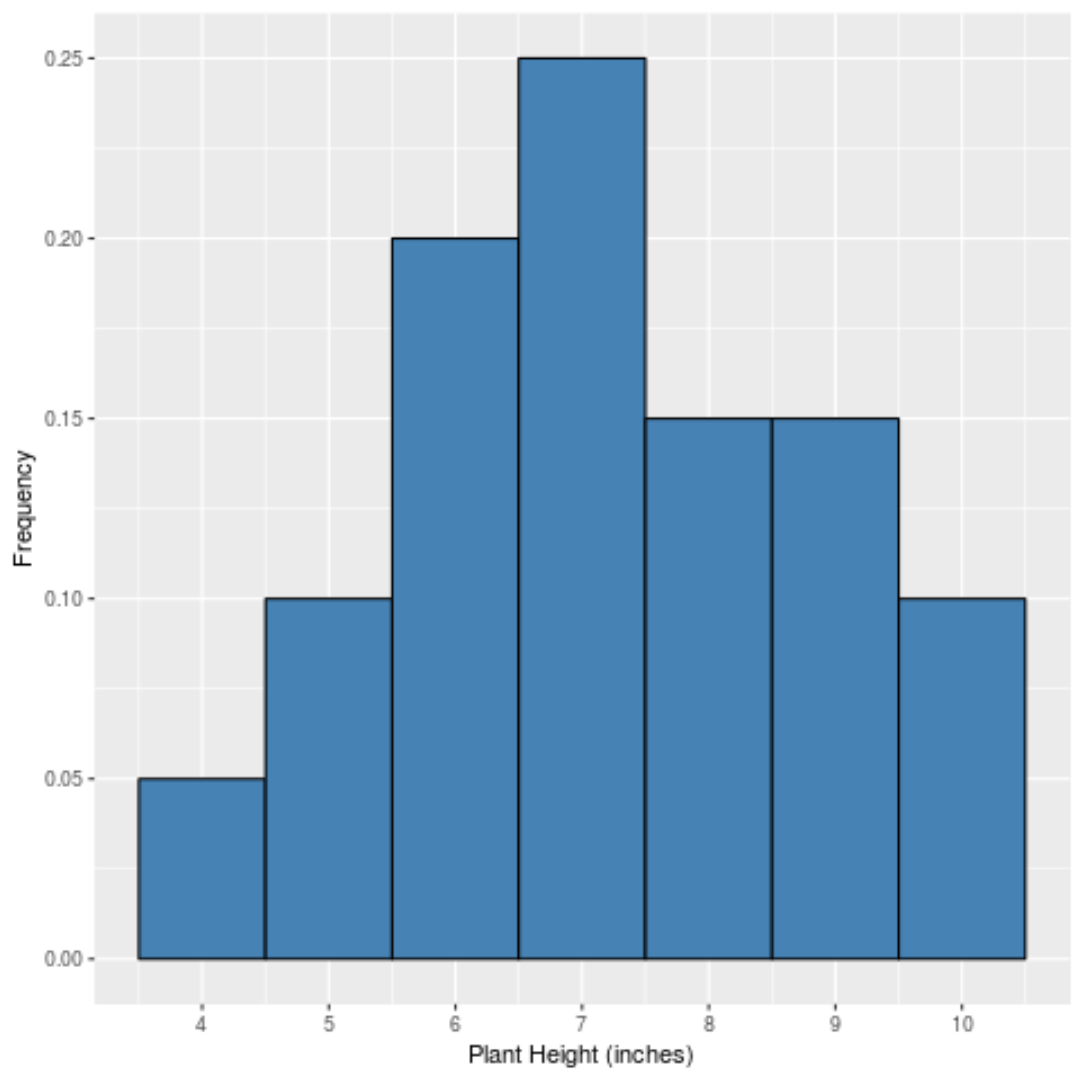
Oś x pokazuje wartość danych, a oś y pokazuje częstotliwość względną (na przykład wartość „7” pojawia się 5 razy na 20 całkowitych wartości w zbiorze danych, więc ma częstotliwość względną 25% lub 0,25 .

A gdybyśmy stworzyli krzywą gęstości , aby uchwycić „kształt” tego rozkładu, wyglądałaby tak:

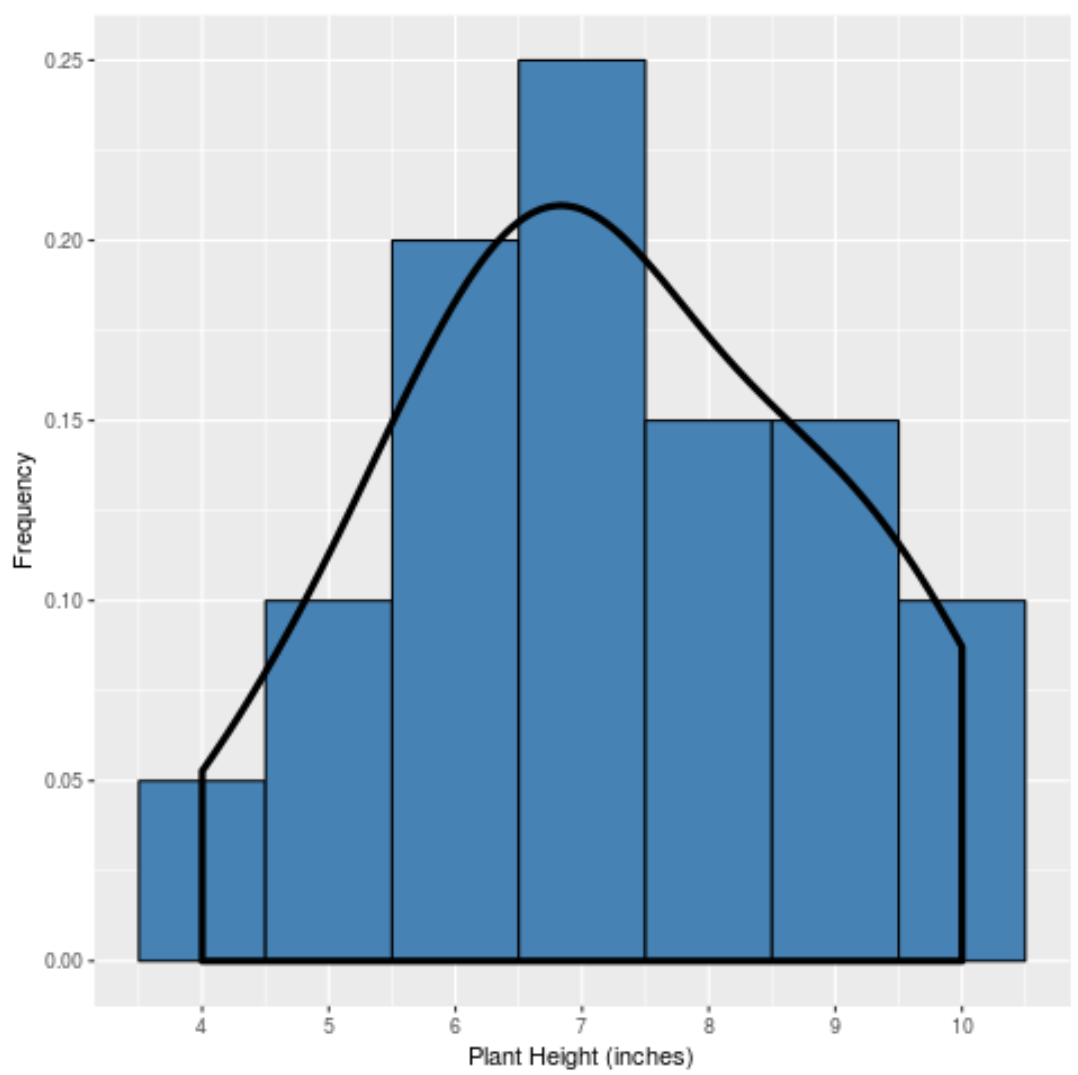
Krzywa jest najwyższa w pobliżu środka rozkładu, ponieważ tam znajduje się większość wartości. Jest również najniższy w pobliżu końców rozkładu, ponieważ mniej roślin przyjmuje te wartości (np. wysokość 4 cali lub 10 cali).

Jak interpretować krzywe gęstości

Krzywe gęstości mają różne kształty i rozmiary i pozwalają nam szybko uzyskać wizualne zrozumienie rozkładu wartości w danym zbiorze danych. Są one szczególnie przydatne, gdy pomagają nam wizualizować:

1. Asymetria

Skośność to sposób opisu symetrii rozkładu. Krzywe gęstości pozwalają nam szybko sprawdzić, czy wykres jest przechylony w lewo, w prawo, czy nie ma przechylenia:

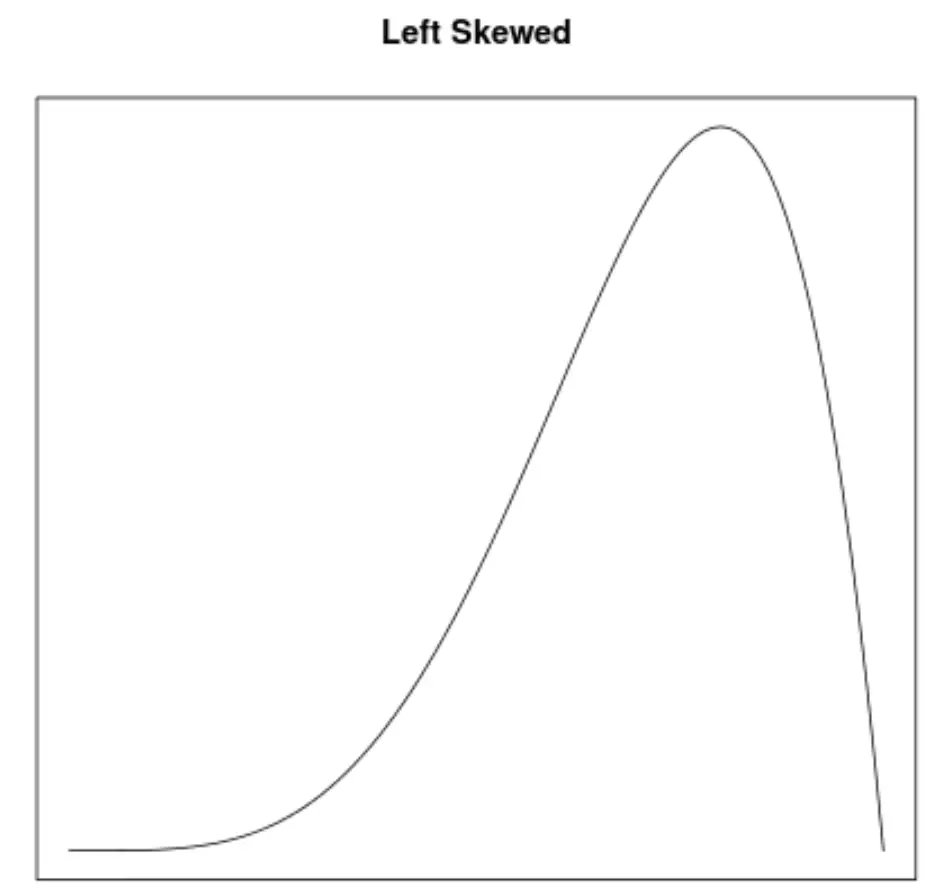
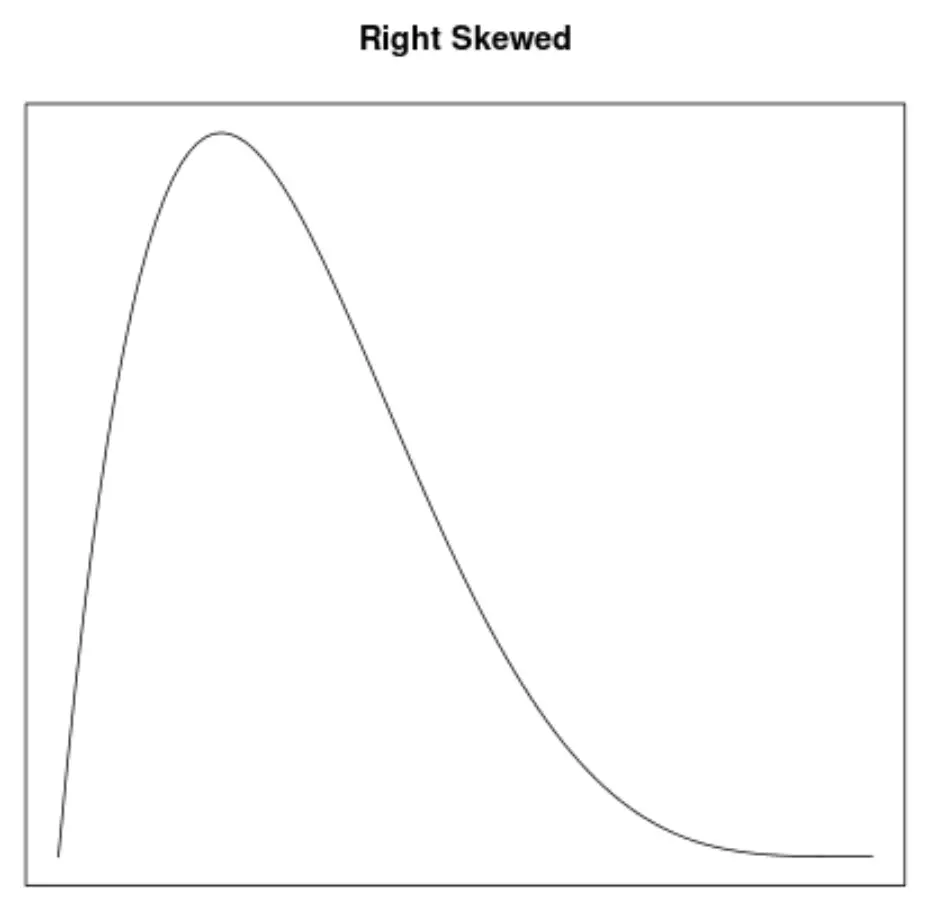
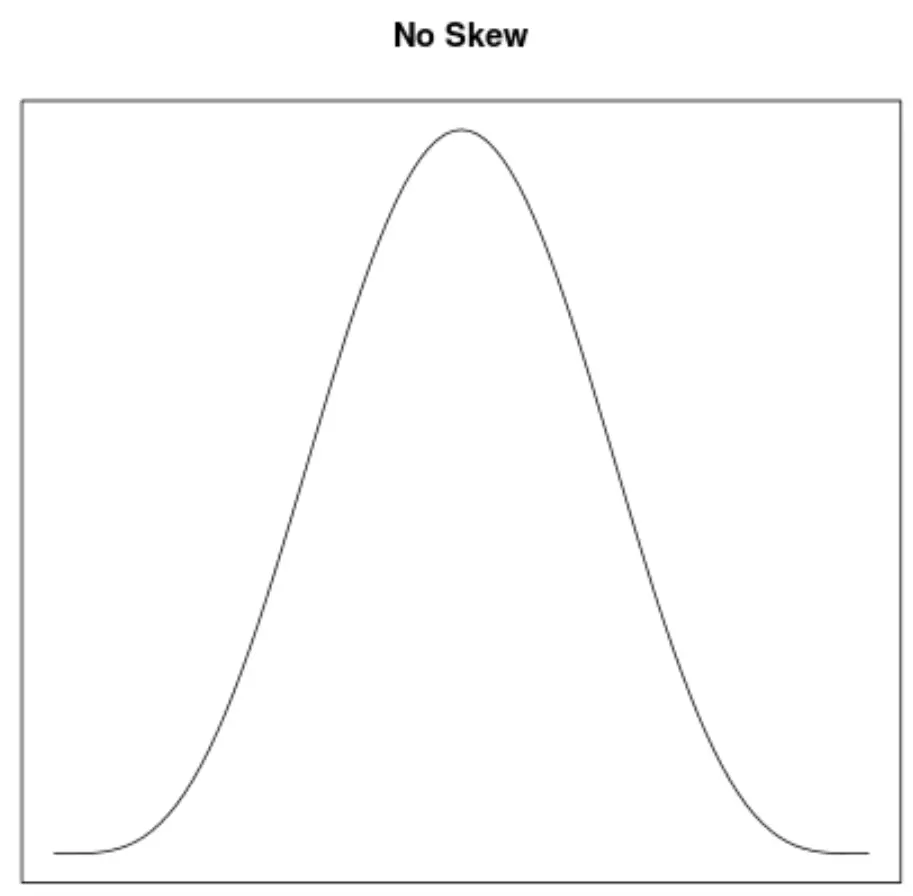
2. Położenie średniej i mediany

Na podstawie skośności krzywej gęstości możemy szybko stwierdzić, czy w danym rozkładzie większa jest średnia czy mediana. Zwłaszcza:

• Jeżeli krzywa gęstości pozostaje asymetryczna , to średnia jest niższa od mediany.
• Jeśli krzywa gęstości jest prawostronnie skośna , to średnia jest większa od mediany.
• Jeśli krzywa gęstości nie ma asymetrii , to średnia jest równa medianie.

3. Liczba pików

Krzywe gęstości pozwalają także szybko sprawdzić, ile „szczytów” znajduje się w danym rozkładzie. W każdym z powyższych przykładów rozkłady miały tylko jeden pik, więc opisalibyśmy te rozkłady jako jednomodalne .

Jednakże niektóre rozkłady mogą mieć dwa piki, które nazywamy rozkładami bimodalnymi . W rzadkich przypadkach możemy również mieć rozkłady multimodalne z dwoma lub większą liczbą pików.

Tworząc po prostu krzywą gęstości dla danego zbioru danych, możemy szybko sprawdzić, ile pików znajduje się w rozkładzie.

Właściwości krzywych gęstości

Krzywe gęstości mają następujące właściwości:

• Pole pod krzywą zawsze sumuje się do 100%.
• Krzywa nigdy nie spadnie poniżej osi x.

Należy pamiętać o tych dwóch faktach podczas tworzenia lub interpretowania krzywych gęstości dla różnych rozkładów.

Dodatkowe zasoby

Wprowadzenie do histogramów częstotliwości względnej
Jak utworzyć krzywą dzwonową w programie Excel
Jak utworzyć krzywą dzwonową w Pythonie