Jak obliczyć skośność i kurtozę w r

W statystyce skośność i kurtoza to dwa sposoby pomiaru kształtu rozkładu.

Skośność jest miarą skośności rozkładu. Wartość ta może być dodatnia lub ujemna.

• Ujemna skośność wskazuje, że ogon znajduje się po lewej stronie rozkładu, który rozciąga się w stronę bardziej ujemnych wartości.
• Dodatnie pochylenie wskazuje, że ogon znajduje się po prawej stronie rozkładu, który rozciąga się w kierunku bardziej dodatnich wartości.
• Wartość zero oznacza, że w rozkładzie nie ma asymetrii, co oznacza, że rozkład jest doskonale symetryczny.

Kurtoza jest miarą tego, czy rozkład jest ciężki czy lekki w porównaniu z rozkładem normalnym .

• Kurtoza rozkładu normalnego wynosi 3.
• Jeśli dany rozkład ma kurtozę mniejszą niż 3, nazywa się go playkurtycznym , co oznacza, że ma tendencję do tworzenia mniejszej liczby i mniej skrajnych wartości odstających niż rozkład normalny.
• Jeśli dany rozkład ma kurtozę większą niż 3, nazywa się go leptokurtycznym , co oznacza, że ma tendencję do tworzenia większej liczby wartości odstających niż rozkład normalny.

Uwaga: W niektórych wzorach (definicja Fishera) od kurtozy odejmuje się 3, aby ułatwić porównanie z rozkładem normalnym. Stosując tę definicję, rozkład miałby większą kurtozę niż rozkład normalny, gdyby miał wartość kurtozy większą niż 0.

W tym samouczku wyjaśniono, jak obliczyć zarówno skośność, jak i kurtozę danego zbioru danych w R.

Przykład: Skośność i spłaszczenie w R

Załóżmy, że mamy następujący zbiór danych:

 data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)

Możemy szybko zwizualizować rozkład wartości w tym zbiorze danych, tworząc histogram:

 hist(data, col=' steelblue ') 

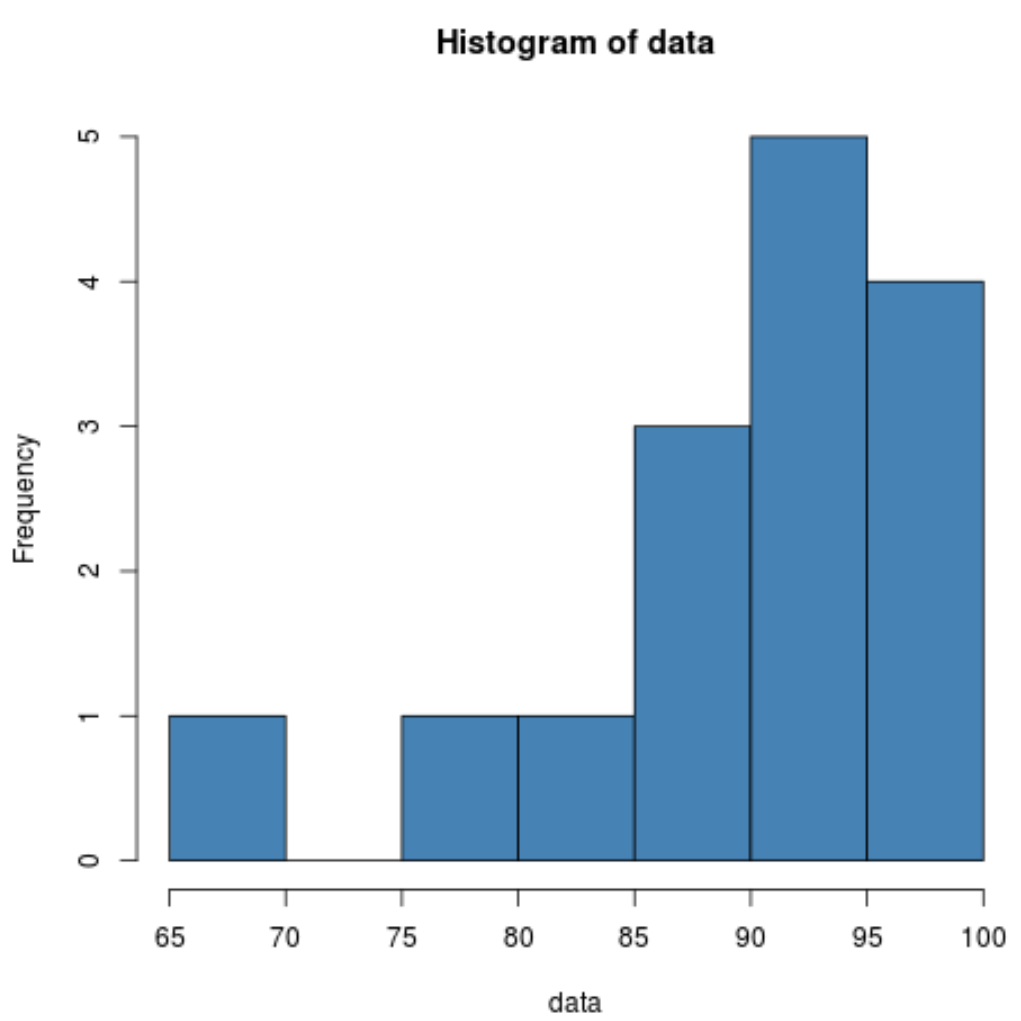
Histogram pokazuje, że rozkład wydaje się być przesunięty w lewo. Oznacza to, że większa część wartości koncentruje się po prawej stronie rozkładu.

Aby obliczyć skośność i kurtozę tego zbioru danych, możemy użyć funkcji skośności() i kurtosis() z biblioteki moment w R:

 library (moments)

#calculate skewness
skewness(data)

[1] -1.391777

#calculate kurtosis
kurtosis(data)

[1] 4.177865

Skośność wynosi -1,391777 , a kurtoza wynosi 4,177865 .

Ponieważ skośność jest ujemna, oznacza to, że rozkład pozostaje skośny. Potwierdza to to, co widzieliśmy na histogramie.

Ponieważ kurtoza jest większa niż 3, oznacza to, że rozkład ma więcej wartości w ogonach w porównaniu z rozkładem normalnym.

Biblioteka momentów oferuje także funkcję jarque.test() , która przeprowadza test dobroci dopasowania, który określa, czy przykładowe dane wykazują skośność i kurtozę zgodną z rozkładem normalnym. Hipotezy zerowe i alternatywne tego testu są następujące:

Hipoteza zerowa : zbiór danych ma skośność i kurtozę odpowiadające rozkładowi normalnemu.

Hipoteza alternatywna : zbiór danych ma skośność i kurtozę, które nie odpowiadają rozkładowi normalnemu.

Poniższy kod pokazuje, jak wykonać ten test:

 jarque.test(data)

	Jarque-Bera Normality Test

data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater

Wartość p testu wynosi 0,05756 . Ponieważ wartość ta jest nie mniejsza niż α = 0,05, nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby stwierdzić, że ten zbiór danych ma skośność i kurtozę różniące się od rozkładu normalnego.

Pełną dokumentację Biblioteki Moments można znaleźć tutaj .

Bonus: kalkulator skośności i kurtozy

Można także obliczyć skośność dla danego zbioru danych, korzystając ze statystycznego kalkulatora skośności i kurtozy , który automatycznie oblicza skośność i kurtozę dla danego zbioru danych.