Jak obliczyć kwartyle dla pogrupowanych danych

Kwartyle to wartości dzielące zbiór danych na cztery równe części.

Aby obliczyć kwartyle dla pogrupowanych danych, możesz użyć następującego wzoru:

Q _i = L + (C/F) * (iN/4 – M)

Złoto:

• L : Dolna granica przedziału zawierającego i- ^ty kwartyl
• C : Szerokość klasy
• F : Częstotliwość przedziału zawierającego i- ^ty kwartyl
• N : Całkowita częstotliwość
• M : Skumulowana częstotliwość prowadząca do przedziału zawierającego i- ^ty kwartyl

Poniższy przykład pokazuje, jak zastosować tę formułę w praktyce.

Przykład: Oblicz kwartyle dla pogrupowanych danych

Załóżmy, że mamy następujący rozkład częstotliwości:

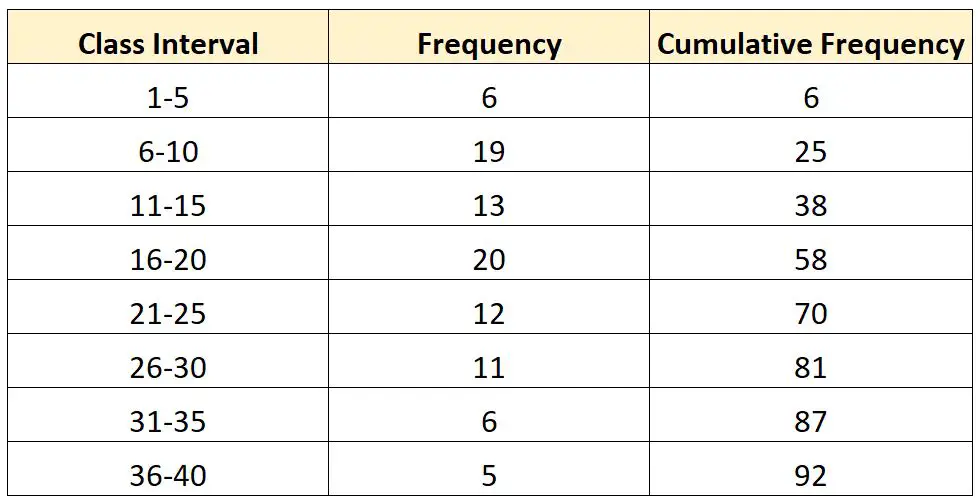
Załóżmy teraz, że chcemy obliczyć wartość trzeciego kwartyla (Q ₃ ) tego rozkładu.

Wartość trzeciego kwartyla będzie znajdować się na pozycji (iN/4) w rozkładzie.

Zatem (iN/4) = (3*92/4) = 69.

Przedział zawierający trzeci kwartyl będzie przedziałem 21–25 , ponieważ 69 leży pomiędzy skumulowanymi częstotliwościami 58 i 70.

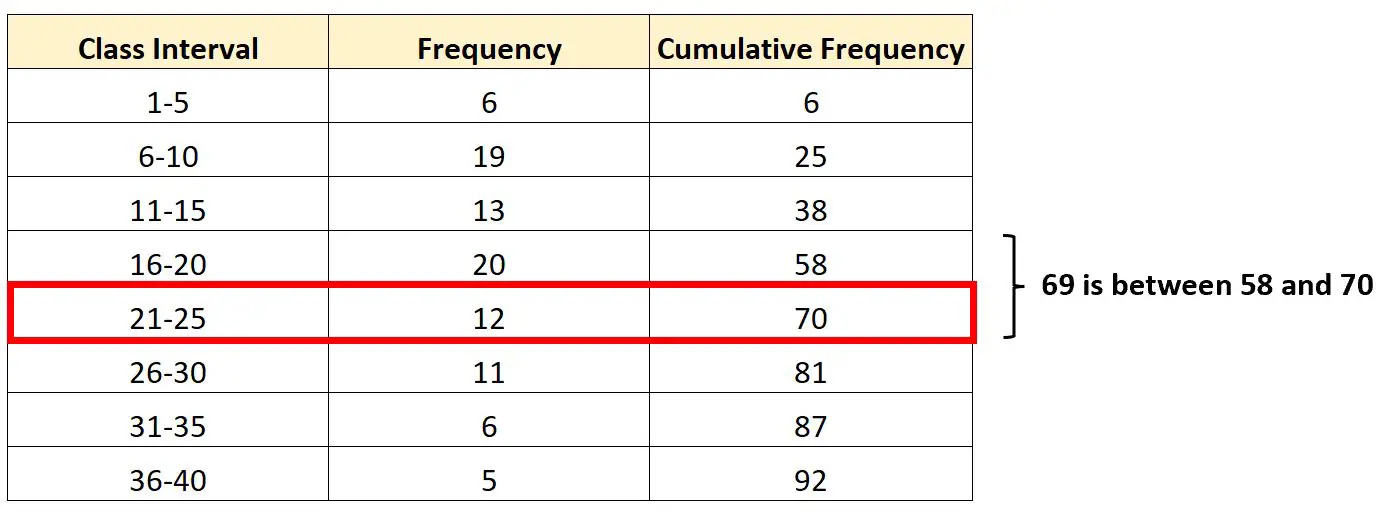
Wiedząc o tym, możemy znaleźć każdą z niezbędnych wartości do wstawienia do naszej formuły:

L : Dolna granica przedziału zawierającego i- ^ty kwartyl

• Dolna granica przedziału wynosi 21 .

C : Szerokość klasy

• Szerokość klasy oblicza się w następujący sposób: 25 – 21 = 4 .

F : Częstotliwość przedziału zawierającego i- ^ty kwartyl

• Częstotliwość zajęć w klasach 21-25 wynosi 12

N : Całkowita częstotliwość

• Całkowita skumulowana częstotliwość w tabeli wynosi 92 .

M : Skumulowana częstotliwość prowadząca do przedziału zawierającego i- ^ty kwartyl

• Częstotliwość skumulowana do klasy 21-25 wynosi 58 .

Możemy następnie podłączyć wszystkie te wartości do poprzedniego wzoru, aby znaleźć wartość w trzecim kwartylu:

• Q _i = L + (C/F) * (iN/4 – M)
• Q ₃ = 21 + (4/12) * ((3)(92)/4 – 58)
• _Q3 = 24,67

Wartość w trzecim kwartylu wynosi 24,67 .

Podobne podejście można zastosować do obliczenia wartości pierwszego i drugiego kwartyla.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat pracy z pogrupowanymi danymi:

Jak znaleźć średnią i odchylenie standardowe pogrupowanych danych
Jak znaleźć tryb pogrupowanych danych
Jak znaleźć medianę pogrupowanych danych
Zgrupowane lub niezgrupowane rozkłady częstotliwości