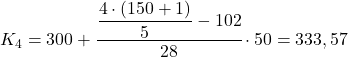Kwintyle (statystyki)
W tym artykule wyjaśniamy, czym są kwintyle i jak są obliczane. Znajdziesz kilka rozwiązanych przykładów obliczania kwintyli, a dodatkowo będziesz mógł obliczyć kwintyle dowolnej próby statystycznej za pomocą kalkulatora online.
Co to są kwintyle?
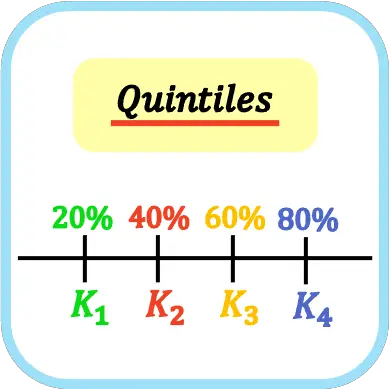
W statystyce kwintyle to cztery wartości dzielące zbiór danych na pięć równych części. Zatem pierwszy, drugi, trzeci i czwarty kwintyle reprezentują odpowiednio 20%, 40%, 60% i 80% danych próbki.
Oznacza to, że na przykład wartość trzeciego kwintyla jest wyższa niż 60% wszystkich zebranych danych, ale niższa niż reszta danych.
Symbolem kwintylów jest wielka litera K z indeksem kwintylowym, tzn. pierwszy kwintyl to K 1 , drugi kwintyl to K 2 , trzeci kwintyl to K 3 i czwarty kwintyl to K 4 . Chociaż może być również reprezentowany przez literę Q (niezalecane, ponieważ powoduje zamieszanie z kwartylami).
👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć kwintyle dla dowolnego zbioru danych.
Kwintyle są miarą pozycji niecentralnej wraz z kwartylami, decylami i percentylami. Jeśli jesteś bardziej zainteresowany, możesz sprawdzić, co oznacza każdy z tych typów kwantyli na naszej stronie internetowej.
Należy zauważyć, że kwintyl może mieć inną definicję. W ekonomii kwintyle reprezentują odsetek populacji uporządkowany według dochodów, lub innymi słowy, porządkują populację według poziomów dochodów. Na przykład pierwszy kwintyl odpowiada 20% najbiedniejszych osób w populacji, drugi kwintyl odpowiada 40% populacji o najniższych dochodach i tak dalej.
Jak obliczyć kwintyle
Aby obliczyć położenie kwintyli próby lub populacji statystycznej, należy pomnożyć liczbę kwintyli przez sumę całkowitej liczby danych plus jeden i podzielić wynik przez pięć.
Zatem wzór na kwintyle wygląda następująco:
![]()
Uwaga: wynik tego wzoru informuje nas o pozycji kwintyla, a nie o jego wartości. Kwintylem będą zatem dane znajdujące się na pozycji otrzymanej ze wzoru.
Czasami jednak wynik tej formuły da nam liczbę dziesiętną, dlatego musimy rozróżnić dwa przypadki w zależności od tego, czy wynik jest liczbą dziesiętną, czy nie:
- Jeżeli wynikiem wzoru jest liczba bez części dziesiętnej , kwintylem są dane znajdujące się na pozycji określonej we wzorze powyżej.
- Jeśli wynikiem wzoru jest liczba z częścią dziesiętną , wartość kwintyla oblicza się za pomocą następującego wyrażenia:
![]()
Gdzie x i oraz x i+1 to numery pozycji, pomiędzy którymi znajduje się liczba uzyskana według pierwszego wzoru, a d to część dziesiętna liczby uzyskanej według pierwszego wzoru.
Jeśli przestraszyłeś się, gdy zobaczyłeś tak wiele kroków pozwalających określić kwintyle zbioru danych, nie martw się, jest to całkiem proste. Przeczytaj poniższe dwa przykłady, a na pewno zrozumiesz znacznie lepiej.
Uwaga : społeczność statystyczna nadal nie jest do końca zgodna co do sposobu obliczania kwintyli, więc możesz znaleźć książkę, która wyjaśnia to nieco inaczej.
Przykłady obliczania kwintyli
Poniżej przedstawiamy dwa ćwiczenia rozwiązane krok po kroku, jak uzyskać kwintyle z serii danych. Zatem, abyście mogli zobaczyć dwa możliwe przypadki, w pierwszym ćwiczeniu wyniki nie są dziesiętne, a w drugim – tak.
Przykład 1
- Oblicz kwintyle następujących serii danych:

Jak widzieliście w powyższym wyjaśnieniu, wzór na położenie kwintyli jest następujący:
![]()
Parametr n odnosi się do całkowitej liczby danych, która wynosi 49, więc aby znaleźć pozycję pierwszego kwintyla, musimy zastąpić n przez 49, a k przez 1:
![]()
Ze wzoru otrzymaliśmy liczbę 10, co oznacza, że kwintyl znajduje się na dziesiątej pozycji uporządkowanej listy, co odpowiada danym 205.
Aby obliczyć drugi kwintyl, należy użyć tego samego wzoru, ale zastępując k przez 2:
![]()
Drugi kwintyl znajduje się zatem na pozycji numer 20 uporządkowanej listy, czyli na wartości 236.
Ponownie powtarzamy proces, aby określić kwintyl 3, ale logicznie rzecz biorąc, teraz zastępujemy k 3:
![]()
Zatem trzeci kwintyl to dane znajdujące się na pozycji 30, co odpowiada 266.
Na koniec ponownie stosujemy wzór, aby obliczyć czwarty kwintyl:
![]()
Czwarty kwintyl znajduje się zatem na pozycji 40, zatem czwarty kwintyl to 286.
Przykład 2
- Oblicz cztery kwintyle danych statystycznych zebranych w poniższej tabeli:

Podobnie jak w poprzednim przykładzie, aby obliczyć położenie kwintyli należy skorzystać ze wzoru:
![]()
W tym przypadku wielkość próby wynosi 42 obserwacje, więc aby znaleźć położenie pierwszego kwintyla, musimy zastąpić parametr n liczbą 42, a k wartością 1:
![]()
Jednak w przeciwieństwie do pierwszego przykładu, tym razem formuła podaje nam liczbę dziesiętną, dlatego aby obliczyć dokładny kwintyl, musimy zastosować następujący wzór:
![]()
Liczba uzyskana z pierwszego wzoru wynosi 8,6, zatem pierwszy kwintyl znajduje się pomiędzy ósmą a dziewiątą daną, czyli odpowiednio 78 i 79. Zatem x i wynosi 78, x i+1 wynosi 79, a d jest częścią dziesiętną otrzymanej liczby, tj. 0,6.
![]()
Teraz wykonujemy dokładnie tę samą procedurę ponownie, aby znaleźć drugi kwintyl. Najpierw obliczamy jego położenie:
![]()
Ale ze wzoru otrzymujemy liczbę dziesiętną pomiędzy 17 a 18 tak, że drugi kwintyl będzie pomiędzy pozycjami siedemnastą a osiemnastą, których wartości odpowiadają odpowiednio 109 i 112 z uporządkowanej listy. Dlatego w procesie stosujemy drugi wzór, aby określić dokładną wartość kwintyla:
![]()
Powtarzamy metodę, aby otrzymać trzeci kwintyl, najpierw określamy jego położenie:
![]()
Obliczona liczba 25,8 oznacza, że wartość kwintyla będzie znajdować się pomiędzy dwudziestą piątą a dwudziestą szóstą pozycją, której wartości wynoszą 134 i 141. Obliczenie dokładnej wartości kwintyla wygląda zatem następująco:
![]()
Na koniec powtarzamy tę samą procedurę po raz ostatni, aby obliczyć kwintyl 4. Najpierw znajdujemy jego położenie:
![]()
Dokładna wartość czwartego kwintyla będzie zatem wynosić od 34 do 35, których pozycje odpowiadają danym 172 i 179. Obliczenie czwartego kwintyla jest zatem następujące:
![]()
Kalkulator kwintyla
Wprowadź zestaw danych statystycznych do poniższego kalkulatora, aby obliczyć kwintyle. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.
Kwintyle w danych pogrupowanych
Aby obliczyć kwintyle, gdy dane są pogrupowane w przedziały, należy najpierw znaleźć jego przedział lub klasę, korzystając z następującego wzoru:
![]()
Kwintyl będzie zatem znajdował się w przedziale, którego częstotliwość bezwzględna jest bezpośrednio większa niż liczba uzyskana za pomocą poprzedniego wyrażenia.
Kiedy już znamy przedział, do którego należy kwintyl, musimy zastosować następujący wzór, aby znaleźć dokładną wartość kwintyla:
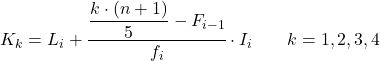
Złoto:
- L i jest dolną granicą przedziału, w którym znajduje się kwintyl.
- n to całkowita liczba obserwacji.
- F i-1 jest skumulowaną częstotliwością bezwzględną poprzedniego przedziału.
- f i jest częstotliwością bezwzględną przedziału, w którym znajduje się kwintyl.
- I i jest szerokością przedziału kwintylowego.
Aby zobaczyć, jak to się robi, oto rozwiązany przykład obliczania kwintyli następujących serii danych pogrupowanych w przedziały:
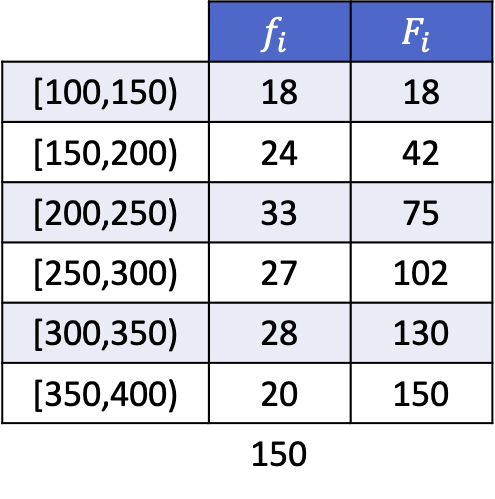
Ponieważ dane są pogrupowane, do obliczenia kwintyla musimy zastosować następującą metodę: najpierw określ zakres, w jakim mieści się kwintyl, a następnie znajdź dokładną wartość kwintyla.
Zatem, aby znaleźć przedział, w którym znajduje się pierwszy kwintyl, stosujemy następujący wzór:
![]()
![]()
Pierwszy kwintyl będzie w przedziale, którego skumulowana częstotliwość bezwzględna jest bezpośrednio większa niż 30,2, w tym przypadku jest to przedział [150,200), którego skumulowana częstotliwość bezwzględna wynosi 42. Kiedy już znamy przedział kwintylowy, stosujemy drugi wzór na proces w celu ustalenia jego dokładnej wartości:
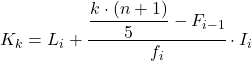
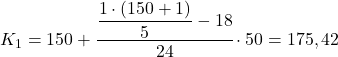
Teraz powtarzamy tę samą procedurę, aby otrzymać drugi kwintyl, najpierw obliczając przedział, w którym się on znajduje:
![]()
Skumulowana częstotliwość bezwzględna bezpośrednio powyżej 60,4 wynosi 75, więc drugi zakres kwintylowy wynosi [200–250). Dlatego podstawiamy odpowiednie wartości do drugiego wzoru, aby obliczyć dokładną wartość kwintyla:
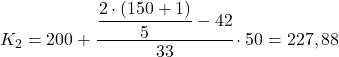
Tę samą procedurę wykonujemy po raz trzeci, aby otrzymać kwintyl 3. Najpierw określamy przedział, w którym znajduje się kwintyl:
![]()
Kwintyl znajduje się w przedziale [250 300), ponieważ jego skumulowana częstotliwość bezwzględna (102) jest bezpośrednio powyżej 90,6. Obliczenie dokładnej wartości trzeciego kwintyla wygląda zatem następująco:
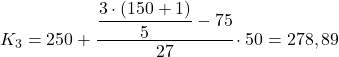
Wreszcie znajdziemy czwarty kwintyl. Jak zawsze, najpierw znajdujemy jego przedział:
![]()
Przedział, którego częstotliwość bezwzględna jest bezpośrednio większa niż 120,8, wynosi [300,350), którego wartość wynosi 130. Dokładna wartość czwartego kwintyla będzie zatem wynosić: