Granice kontrolne

Przez Benjamin Anderson 2 sierpnia, 2023 Zarządzanie jakością 0 komentarzy

W tym artykule wyjaśniono, czym jest granica kontrolna i jakie są różne granice kontrolne na karcie kontrolnej. Zobaczysz także sposób obliczania granic kontrolnych oraz praktyczny przykład wyznaczania granic kontrolnych procesu.

Co to są granice kontrolne?

Granice kontrolne to poziome linie na karcie kontrolnej, które służą do określenia, czy proces jest kontrolowany, czy nie.

Na karcie kontrolnej znajdują się dwie granice kontrolne: górna i dolna granica kontrolna, które wyznaczają obszar kontrolny odpowiednio powyżej i poniżej.

Zatem granice kontrolne to wartości służące do wskazania obszaru kontroli procesu. Jeżeli pomiar uzyskany z procesu mieści się w granicach kontrolnych, oznacza to, że proces jest kontrolowany. W przeciwnym razie należy sprawdzić maszynę lub proces, ponieważ prawdopodobnie uległy odchyleniom.

Rodzaje granic kontrolnych

Granice kontrolne to:

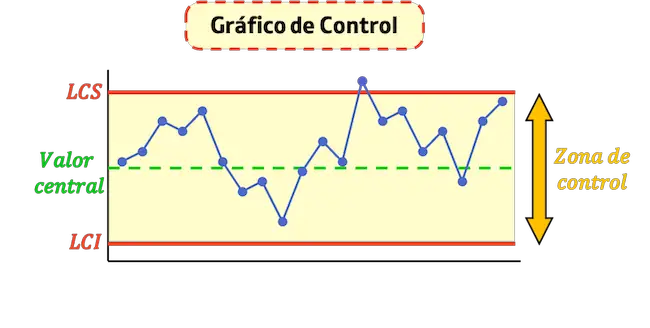
Górna granica kontrolna (LCS) : jest to linia wskazująca maksymalną wartość akceptowaną w procesie.
Dolna granica kontrolna (LCI) : Jest to linia wskazująca minimalną wartość akceptowaną w procesie.
Centralna linia kontrolna : Jest to linia przedstawiająca średnią wartość wykresu. Im bliżej tej linii znajdują się punkty, tym proces jest bardziej stabilny.

Jak obliczyć limity kontrolne

Obecnie granice kontrolne procesu są na ogół obliczane za pomocą oprogramowania komputerowego, które umożliwia kontrolowanie procesu. Jednak ważne jest również, aby wiedzieć, w jaki sposób są one obliczane, ponieważ może być konieczne znalezienie ich ręcznie.

Obliczanie granic kontrolnych karty kontrolnej zależy od rodzaju wykresu, który chcesz utworzyć, ponieważ wartości będą się zmieniać w zależności od tego, czy jest to karta kontrolna dla średniej, czy dla zakresu.

Średni wykres kontrolny to wykres, na którym ocenia się ewolucję średniej procesu. Zatem średnią zestawu wartości oblicza się za pomocą następującego wzoru:

$\overline{X}=\cfrac{\displaystyle \sum_{i=1}^n x_i}{n}$

Złoto:

$x_i$

jest numerem taktu i.
$n$

to liczba wykonanych pomiarów.

Wyznaczymy centralną wartość wykresu kontrolnego dla średniej jako

$\overline{\overline{X}}$

, który jest średnią próbek i jest obliczany za pomocą następującego wyrażenia:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}$

Złoto:

$\overline{X}_j$

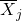
jest średnią próbki j.
$m$

to liczba pobranych próbek.

➤ Patrz: Obliczanie średniej arytmetycznej

Natomiast centralną wartością wykresu kontroli zasięgu jest średnia zasięgu wszystkich pobranych próbek:

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}$

Złoto:

$R_j$

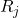
jest zakresem próbki j.
$m$

to liczba pobranych próbek.

➤ Zobacz: Obliczanie zakresu statystycznego

Zatem wzory na obliczenie granic kontrolnych karty kontrolnej są następujące:

karta kontrolna

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}\end{array}$

Karta kontrolna R

$\begin{array}{c}LCS=D_4\cdot \overline{R}\\[3ex]LCI=D_3\cdot\overline{R}\end{array}$

Gdzie wartości parametrów A ₂ , D ₃ i D ₄ znajdują się w poniższej tabeli:

Rozmiar (nr)	O ₂	Dzień ₃	_J4
2	1880	0,000	3267
3	1023	0,000	2575
4	0,729	0,000	2282
5	0,577	0,000	2115
6	0,483	0,000	2004
7	0,419	0,076	1924
8	0,373	0,136	1864
9	0,337	0,184	1816
dziesięć	0,308	0,223	1777

Przykład obliczenia granic kontrolnych

Przedsiębiorstwo przemysłowe pragnie kontrolować pomiar średnicy cylindra, aby sprawdzić, czy jego proces produkcyjny jest pod kontrolą. Aby to zrobić, należy co 15 minut pobierać próbkę 5 cylindrów i mierzyć ich średnicę. Poniższa tabela przedstawia zapis pomiaru.

Aby znaleźć granice kontrolne, musimy najpierw przyjąć średnią arytmetyczną i zakres każdego zestawu pomiarów:

Obliczmy teraz średnią ze średnich i zakresów, które będą wartościami środkowymi wykresu kontrolnego odpowiednio dla średniej i dla rozstępu:

$\overline{\overline{X}}=\cfrac{\displaystyle \sum_{j=1}^m {\overline{X}_j}}{m}=4,8589$

$\overline{R}=\cfrac{\displaystyle \sum_{j=1}^m R_j}{m}=0,0227$

W tym przypadku każda próbka składa się z 5 pomiarów, dlatego współczynniki wzorów na granicę kontrolną są następujące:

$A_2=0,577$

$D_3=0$

$D_4=2,115$

Obliczamy górną i dolną granicę kontrolną średniej i rozszerzonej karty kontrolnej:

Granice kontrolne karty kontrolnej

$\begin{array}{c}LCS=\overline{\overline{X}}+A_2\cdot \overline{R}=4,8589+0,577\cdot 0,0227=4,8720\\[3ex]LCI=\overline{\overline{X}}-A_2\cdot \overline{R}=4,8589-0,577\cdot 0,0227=4,8458\end{array}$

Granice kontrolne Karta kontrolna R

$\begin{array}{c}LCS=D_4\cdot \overline{R}=2,115\cdot 0,0227=0,0481\\[3ex]LCI=D_3\cdot\overline{R}=0\cdot 0,0227=0\end{array}$

Karty kontrolne ćwiczeń są zatem następujące:

Na pierwszym wykresie kontrolnym widzimy, że dwie wartości są mniejsze od dolnej granicy kontrolnej. Dodatkowo na drugiej karcie kontrolnej również znajduje się wartość powyżej górnej granicy kontrolnej. Dlatego proces nie jest kontrolowany.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Co to są granice kontrolne?

Rodzaje granic kontrolnych

Jak obliczyć limity kontrolne

Przykład obliczenia granic kontrolnych

o autorze

Dr Benjamin Anderson

Dodaj komentarz