Liniowa analiza dyskryminacyjna w r (krok po kroku)

Liniowa analiza dyskryminacyjna to metoda, której można użyć, gdy masz zestaw zmiennych predykcyjnych i chcesz sklasyfikować zmienną odpowiedzi na dwie lub więcej klas.

W tym samouczku przedstawiono krok po kroku przykład przeprowadzania liniowej analizy dyskryminacyjnej w języku R.

Krok 1: Załaduj niezbędne biblioteki

Najpierw załadujemy niezbędne biblioteki dla tego przykładu:

 library (MASS)
library (ggplot2)

Krok 2: Załaduj dane

W tym przykładzie użyjemy zestawu danych iris wbudowanego w R. Poniższy kod pokazuje, jak załadować i wyświetlić ten zestaw danych:

 #attach iris dataset to make it easy to work with
attach(iris)

#view structure of dataset
str(iris)

'data.frame': 150 obs. of 5 variables:
 $ Sepal.Length: num 5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
 $ Sepal.Width: num 3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
 $Petal.Length: num 1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
 $Petal.Width: num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
 $ Species: Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 ...

Widzimy, że zbiór danych zawiera w sumie 5 zmiennych i 150 obserwacji.

Na potrzeby tego przykładu zbudujemy liniowy model analizy dyskryminacyjnej, aby sklasyfikować, do jakiego gatunku należy dany kwiat.

W modelu wykorzystamy następujące zmienne predykcyjne:

• Długość rozdzielacza
• Sepal.Szerokość
• Płatek.Długość
• Płatek.Szerokość

Wykorzystamy je do przewidzenia zmiennej odpowiedzi Gatunek , która obsługuje następujące trzy potencjalne klasy:

• setosa
• wielokolorowy
• Wirginia

Krok 3: Skaluj dane

Jednym z kluczowych założeń liniowej analizy dyskryminacyjnej jest to, że każda ze zmiennych predykcyjnych ma tę samą wariancję. Prostym sposobem zapewnienia spełnienia tego założenia jest skalowanie każdej zmiennej w taki sposób, aby miała średnią 0 i odchylenie standardowe 1.

Możemy to zrobić szybko w R za pomocą funkcjiscale () :

 #scale each predictor variable (ie first 4 columns)
iris[1:4] <- scale(iris[1:4])

Możemy użyć funkcji Apply() , aby sprawdzić, czy każda zmienna predykcyjna ma teraz średnią 0 i odchylenie standardowe 1:

 #find mean of each predictor variable
apply(iris[1:4], 2, mean)

 Sepal.Length Sepal.Width Petal.Length Petal.Width 
-4.484318e-16 2.034094e-16 -2.895326e-17 -3.663049e-17 

#find standard deviation of each predictor variable
apply(iris[1:4], 2, sd) 

Sepal.Length Sepal.Width Petal.Length Petal.Width 
           1 1 1 1

Krok 4: Utwórz próbki szkoleniowe i testowe

Następnie podzielimy zbiór danych na zbiór uczący, na którym będziemy trenować model, oraz zbiór testowy, na którym będziemy testować model:

 #make this example reproducible
set.seed(1)

#Use 70% of dataset as training set and remaining 30% as testing set
sample <- sample(c( TRUE , FALSE ), nrow (iris), replace = TRUE , prob =c(0.7,0.3))
train <- iris[sample, ]
test <- iris[!sample, ] 

Krok 5: Dostosuj model LDA

Następnie skorzystamy z funkcji lda() z pakietu MASS , aby dostosować model LDA do naszych danych:

 #fit LDA model
model <- lda(Species~., data=train)

#view model output
model

Call:
lda(Species ~ ., data = train)

Prior probabilities of groups:
    setosa versicolor virginica 
 0.3207547 0.3207547 0.3584906 

Group means:
           Sepal.Length Sepal.Width Petal.Length Petal.Width
setosa -1.0397484 0.8131654 -1.2891006 -1.2570316
versicolor 0.1820921 -0.6038909 0.3403524 0.2208153
virginica 0.9582674 -0.1919146 1.0389776 1.1229172

Coefficients of linear discriminants:
                    LD1 LD2
Sepal.Length 0.7922820 0.5294210
Sepal.Width 0.5710586 0.7130743
Petal.Length -4.0762061 -2.7305131
Petal.Width -2.0602181 2.6326229

Proportion of traces:
   LD1 LD2 
0.9921 0.0079 

Oto jak interpretować wyniki modelu:

Prawdopodobieństwa a priori grupowe: reprezentują proporcje każdego gatunku w zbiorze uczącym. Na przykład 35,8% wszystkich obserwacji w zbiorze uczącym dotyczyło gatunku virginica .

Średnie grupowe: wyświetlają średnie wartości każdej zmiennej predykcyjnej dla każdego gatunku.

Liniowe współczynniki dyskryminacyjne: przedstawiają liniową kombinację zmiennych predykcyjnych używanych do uczenia reguły decyzyjnej modelu LDA. Na przykład:

• LD1: 0,792 * długość działki + 0,571 * szerokość działki – 4,076 * długość płatka – 2,06 * szerokość płatka
• LD2: 0,529 * długość działki + 0,713 * szerokość działki – 2,731 * długość płatka + 2,63 * szerokość płatka

Proporcja śledzenia: Wyświetla procent separacji osiągnięty przez każdą liniową funkcję dyskryminacyjną.

Krok 6: Użyj modelu do przewidywania

Po dopasowaniu modelu przy użyciu naszych danych treningowych możemy go użyć do przewidywania danych testowych:

 #use LDA model to make predictions on test data
predicted <- predict (model, test)

names(predicted)

[1] "class" "posterior" "x"   

Zwraca to listę z trzema zmiennymi:

• class: przewidywana klasa
• posterior: Prawdopodobieństwo późniejsze , że obserwacja należy do każdej klasy
• x: Dyskryminatory liniowe

Możemy szybko zwizualizować każdy z tych wyników dla pierwszych sześciu obserwacji w naszym testowym zbiorze danych:

 #view predicted class for first six observations in test set
head(predicted$class)

[1] setosa setosa setosa setosa setosa setosa
Levels: setosa versicolor virginica

#view posterior probabilities for first six observations in test set
head(predicted$posterior)

   setosa versicolor virginica
4 1 2.425563e-17 1.341984e-35
6 1 1.400976e-21 4.482684e-40
7 1 3.345770e-19 1.511748e-37
15 1 6.389105e-31 7.361660e-53
17 1 1.193282e-25 2.238696e-45
18 1 6.445594e-22 4.894053e-41

#view linear discriminants for first six observations in test set
head(predicted$x)

         LD1 LD2
4 7.150360 -0.7177382
6 7.961538 1.4839408
7 7.504033 0.2731178
15 10.170378 1.9859027
17 8.885168 2.1026494
18 8.113443 0.7563902

Możemy użyć poniższego kodu, aby sprawdzić, dla jakiego procentu obserwacji model LDA poprawnie przewidział gatunek:

 #find accuracy of model
mean(predicted$class==test$Species)

[1] 1

Okazuje się, że model poprawnie przewidział gatunek dla 100% obserwacji w naszym testowym zbiorze danych.

W prawdziwym świecie model LDA rzadko poprawnie przewiduje wyniki każdej klasy, ale ten zbiór danych tęczówki jest po prostu skonstruowany w taki sposób, że algorytmy uczenia maszynowego zwykle działają bardzo dobrze.

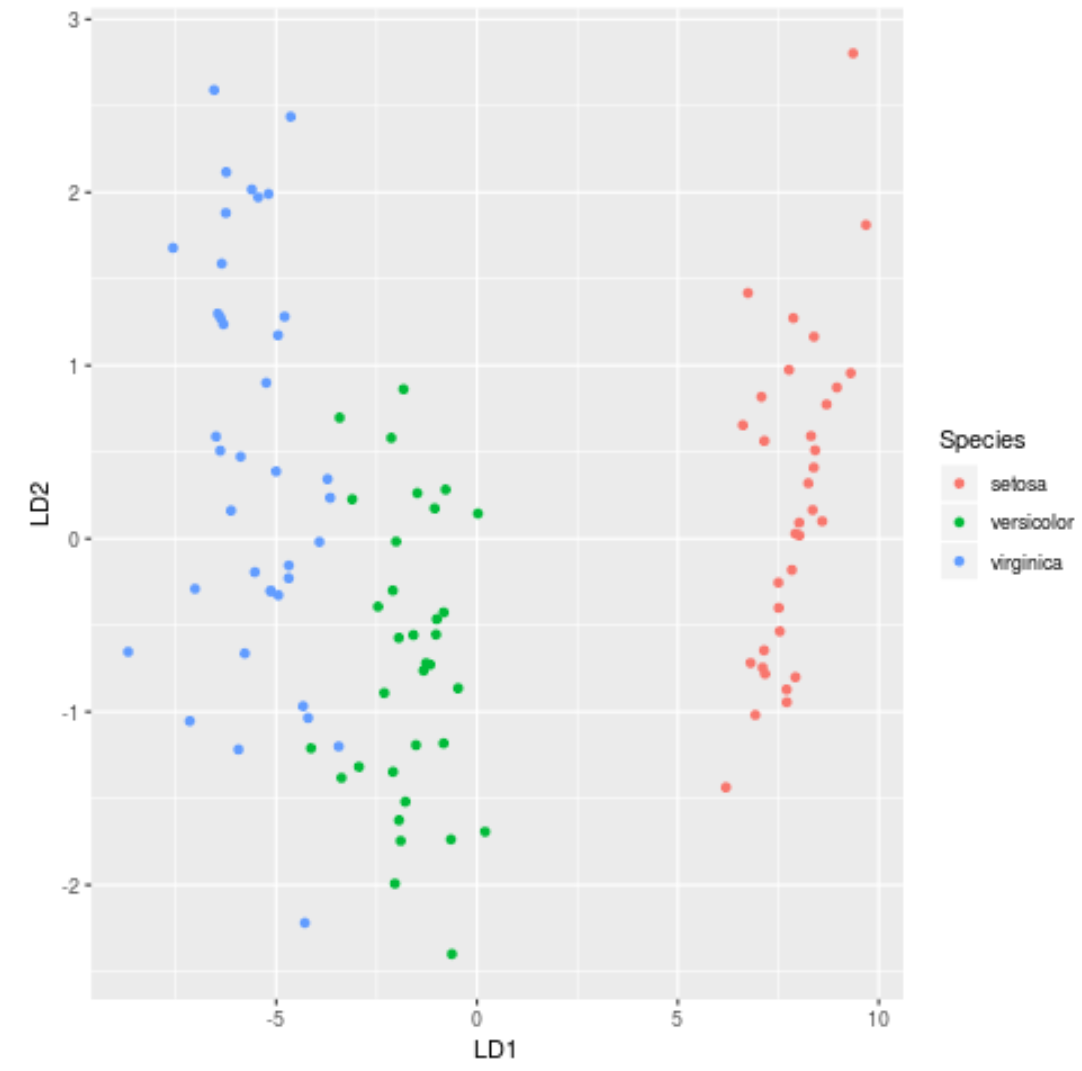
Krok 7: Wizualizuj wyniki

Na koniec możemy utworzyć wykres LDA, aby zwizualizować liniowe wyróżniki modelu i zwizualizować, jak dobrze oddziela on trzy różne gatunki w naszym zbiorze danych:

 #define data to plot
lda_plot <- cbind(train, predict(model)$x)

#createplot
ggplot(lda_plot, aes (LD1, LD2)) +
  geom_point( aes (color=Species))

Pełny kod R użyty w tym samouczku znajdziesz tutaj .