Rozkład lognormalny

Przez Benjamin Anderson 3 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład lognormalny w statystyce. Dowiesz się więc, jakie są właściwości rozkładu lognormalnego i wykres tego typu rozkładu prawdopodobieństwa.

Jaki jest rozkład lognormalny?

Rozkład lognormalny lub rozkład lognormalny to rozkład prawdopodobieństwa definiujący zmienną losową, której logarytm ma rozkład normalny.

Zatem jeśli zmienna X ma rozkład normalny, to funkcja wykładnicza e ^x ma rozkład logarytmiczno-normalny.

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Należy pamiętać, że rozkład lognormalny można zastosować tylko wtedy, gdy wartości zmiennych są dodatnie, ponieważ logarytm jest funkcją, która przyjmuje tylko jeden dodatni argument.

Wśród różnych zastosowań rozkładu lognormalnego w statystyce wyróżniamy wykorzystanie tego rozkładu do analizy inwestycji finansowych i przeprowadzania analiz niezawodności.

Rozkład lognormalny jest również znany jako rozkład Tinauta , czasami zapisywany także jako rozkład lognormalny lub rozkład logarytmiczno-normalny .

Wykres rozkładu lognormalnego

Teraz, gdy znamy definicję rozkładu lognormalnego, w tej sekcji zobaczymy, jak graficzna reprezentacja rozkładu lognormalnego zmienia się w zależności od wartości jego średniej arytmetycznej i odchylenia standardowego.

Wykres funkcji gęstości rozkładu lognormalnego jest następujący:

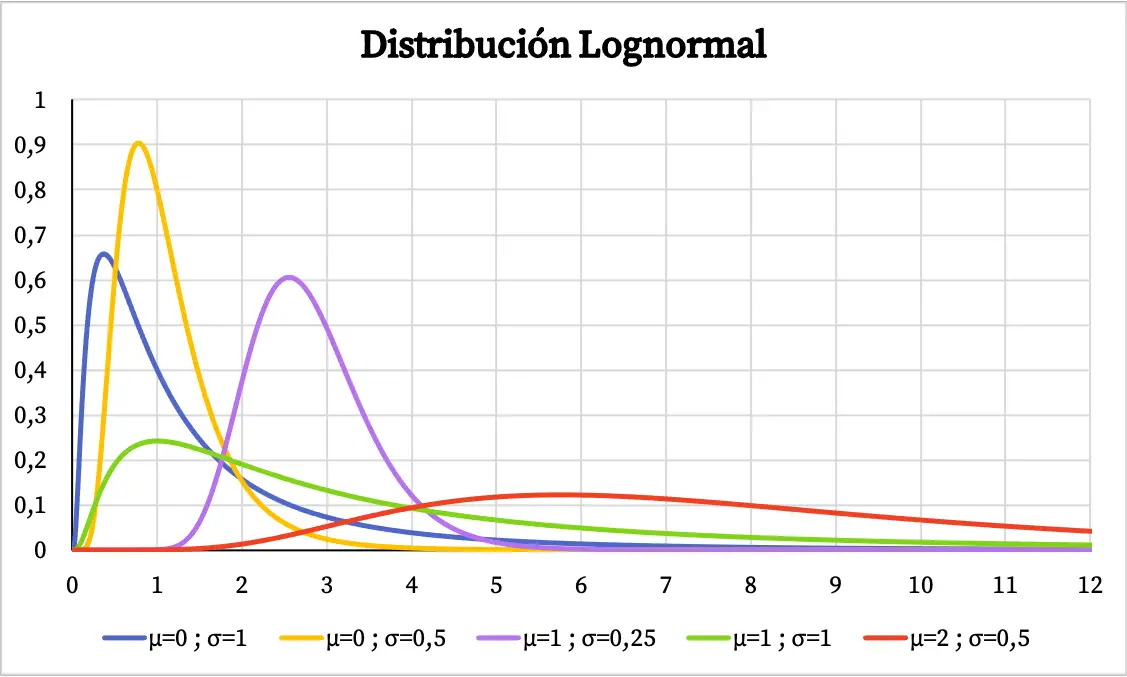
Z drugiej strony skumulowany wykres prawdopodobieństwa rozkładu lognormalnego wygląda następująco:

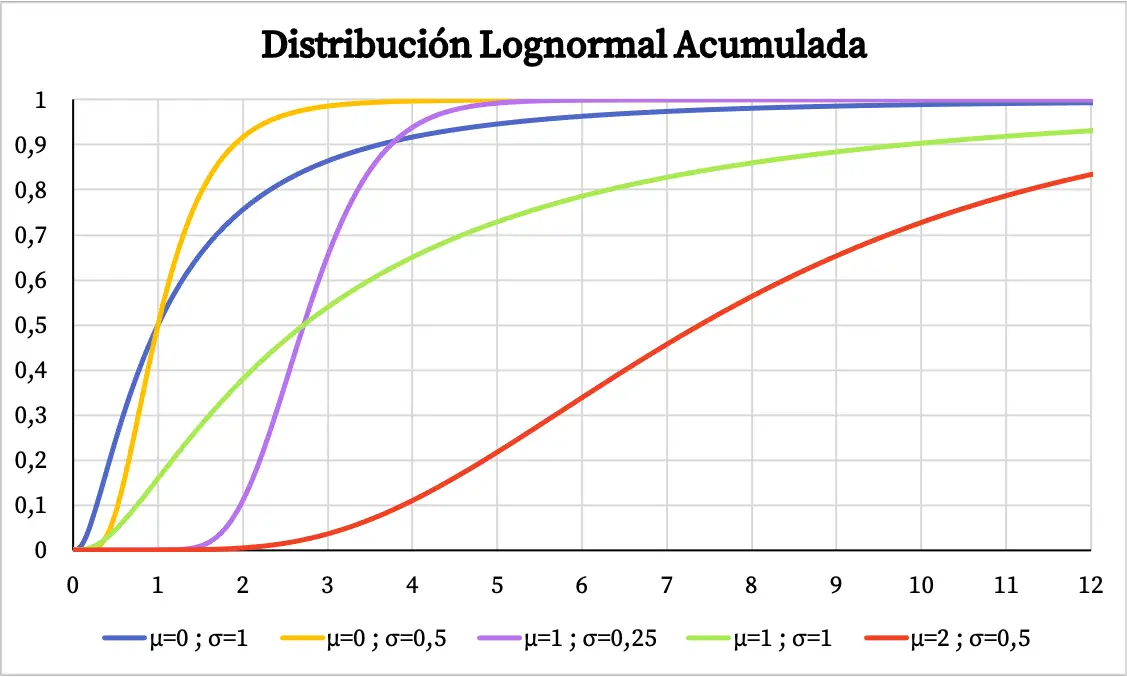
Charakterystyka rozkładu lognormalnego

Rozkład lognormalny ma następujące cechy:

Rozkład lognormalny jest definiowany przez wartość dwóch parametrów, jego średnią arytmetyczną μ i wariancję σ ² .

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Dziedzina rozkładu lognormalnego składa się z dodatnich liczb rzeczywistych, ponieważ logarytm nie przyjmuje wartości ujemnych ani zerowych.

$x\in (0,+\infty)$

Oczekiwanie na rozkład lognormalny jest równe liczbie e podniesionej do sumy średniej plus wariancja podzielonej przez dwa.

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

Z drugiej strony wariancję rozkładu lognormalnego można obliczyć za pomocą następującego wyrażenia:

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

Tryb rozkładu lognormalnego jest równoważny liczbie e podniesionej do średniej rozkładu.

$Mo=e^\mu$

Współczynnik skośności rozkładu lognormalnego można wyznaczyć stosując następujący wzór:

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

Wzór na funkcję gęstości rozkładu lognormalnego to:

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

Wzór na skumulowaną funkcję prawdopodobieństwa rozkładu lognormalnego to:

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

Złoto

$\Phi$

jest skumulowaną funkcją prawdopodobieństwa standardowego rozkładu normalnego .

Średnia arytmetyczna rozkładu lognormalnego jest większa niż wartość jego mediany.

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

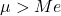
o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Jaki jest rozkład lognormalny?

Wykres rozkładu lognormalnego

Charakterystyka rozkładu lognormalnego

o autorze

Dr Benjamin Anderson

Dodaj komentarz