Jak interpretować skalę i wykres lokalizacji: z przykładami

Skalowany wykres lokalizacji to rodzaj wykresu, który wyświetla dopasowane wartości modelu regresji wzdłuż osi x i pierwiastek kwadratowy reszt standaryzowanych wzdłuż osi y.

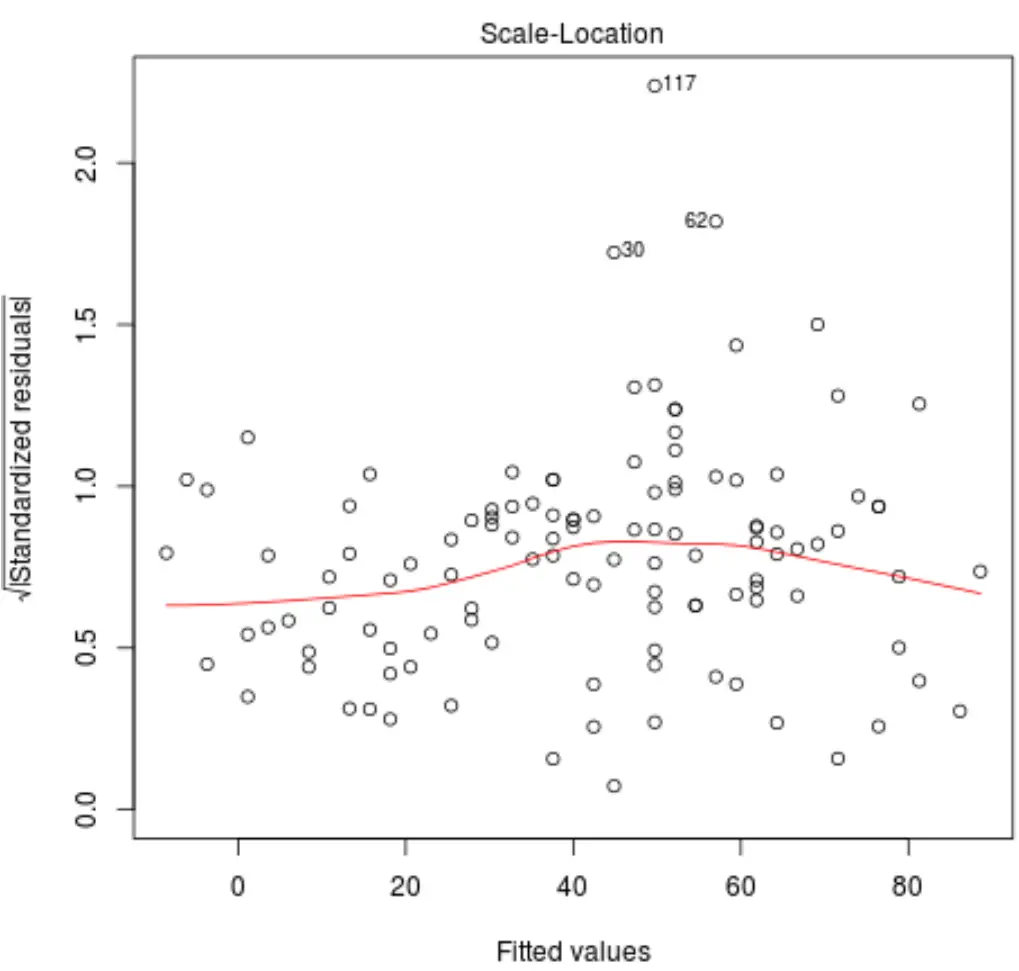
Patrząc na ten wykres, sprawdzamy dwie rzeczy:

1. Sprawdź, czy czerwona linia na wykresie jest w przybliżeniu pozioma. Jeżeli tak jest, to założenie o homoskedastyczności jest prawdopodobnie spełnione dla danego modelu regresji. Oznacza to, że rozkład reszt jest w przybliżeniu równy dla wszystkich dopasowanych wartości.

2. Sprawdź, czy nie ma wyraźnego trendu wśród reszt. Innymi słowy, reszty powinny być losowo rozrzucone wokół czerwonej linii z w przybliżeniu równą zmiennością dla wszystkich dopasowanych wartości.

Wykres skali i lokalizacji w R

Możemy użyć poniższego kodu, aby dopasować prosty model regresji liniowej w języku R i utworzyć wykres skali i lokalizacji dla wynikowego modelu:

 #fit simple linear regression model
model <- lm(Ozone ~ Temp, data = airquality)

#produce scale-location plot
plot(model)

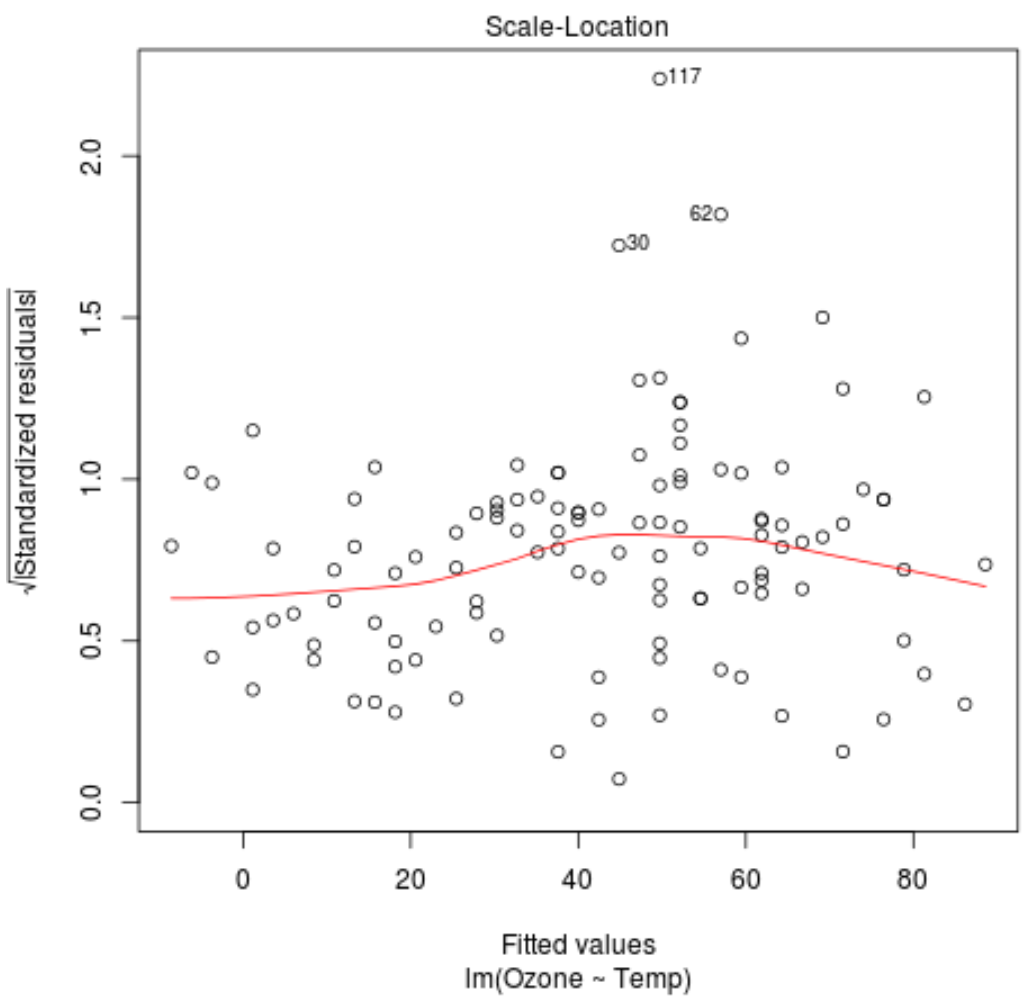
Na wykresie skali i położenia tego modelu regresji możemy zaobserwować dwie następujące rzeczy.

1. Czerwona linia jest w przybliżeniu pozioma na wykresie. Jeżeli tak jest, to dla danego modelu regresji założenie o homoskedastyczności jest spełnione. Oznacza to, że rozkład reszt jest w przybliżeniu równy dla wszystkich dopasowanych wartości.

2. Sprawdź, czy nie ma wyraźnego trendu wśród reszt. Innymi słowy, reszty powinny być losowo rozrzucone wokół czerwonej linii z w przybliżeniu równą zmiennością dla wszystkich dopasowanych wartości.

Uwagi techniczne

Na wykresie zaznaczono trzy obserwacje ze zbioru danych o najwyższych resztach standaryzowanych.

Widzimy, że obserwacje w wierszach 30, 62 i 117 mają najwyższe reszty standaryzowane.

Nie musi to koniecznie oznaczać, że te obserwacje są wartościami odstającymi, ale warto przyjrzeć się oryginalnym danym, aby bliżej przyjrzeć się tym obserwacjom.

Chociaż widzimy, że czerwona linia jest w przybliżeniu pozioma na wykresie lokalizacji skali, służy to jedynie jako wizualny sposób sprawdzenia, czy spełnione jest założenie homoskedastyczności.

Formalnym testem statystycznym, za pomocą którego możemy sprawdzić, czy spełnione jest założenie homoskedastyczności, jest test Breuscha-Pagana .

Test Breuscha-Pagana w R

Poniższy kod pokazuje, jak używać funkcji bptest() pakietu lmtest do wykonania testu Breuscha-Pagana w R:

 #load lmtest package
library(lmtest)

#perform Breusch-Pagan Test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 1.4798, df = 1, p-value = 0.2238

Test Breuscha-Pagana wykorzystuje następujące hipotezy zerowe i alternatywne:

• Hipoteza zerowa (H ₀ ): reszty są homoskedastyczne (tzn. równomiernie rozłożone)
• Hipoteza alternatywna ( _HA ): reszty są heteroskedastyczne (tj. nierównomiernie rozłożone)

Z wyniku widzimy, że wartość p testu wynosi 0,2238 . Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Nie mamy wystarczających dowodów, aby twierdzić, że heteroskedastyczność jest obecna w modelu regresji.

Wynik ten odpowiada naszej wizualnej kontroli czerwonej linii na wykresie lokalizacji skali.

Dodatkowe zasoby

Zrozumienie heteroskedastyczności w analizie regresji
Jak utworzyć wykres rezydualny w R
Jak wykonać test Breuscha-Pagana w R